基于线性预测的多普勒频率估计方法研究
刘志华,党宏杰,陶业荣,杨 潇
(1.中国人民解放军63880部队,河南洛阳471003;2.中国人民解放军63921部队,北京101416)
0 引言
PCM/FM是目前遥测系统中广泛采用的一种编码调制方式。由于这种体制一般用于高速飞行器,所以在信号接收过程中会出现较大的多普勒频率分量。多普勒频率的存在将使载波频率发生漂移,导致信号解调时误码率上升。传统PCM/FM解调的硬件实现过程多采用AFC环路跟踪多普勒频率的变化,再对其进行修正[1]。目前,软件解调中常采用离散短时傅里叶变换(Discrete Short Time Fourier Transform,DSTFT)方法解调PCM/FM信号[2,3]。在进行DSTFT运算前需要估算信号的多普勒频率,以得到DSTFT所需的准确频点。采用DSTFT估算信号的多普勒频率,首先需要搜索信号中存在长连“0”码和长连“1”码,以提高多普勒频率估计精度,因此该方法对数据的要求较高,且运算量较大。
针对以上问题提出了基于线性预测的多普勒频率估计方法,该方法首先采用现代功率谱估计中的线性预测法将一个码元内的数据进行扩展,再对扩展后的数据进行傅里叶分析得到多普勒频率,最后通过Matlab仿真验证了新方法良好的性能。
1 PCM/FM信号解调及多普勒频移校正
由于实际接收到的PCM/FM信号是非平稳随机信号,对非平稳随机信号的处理通常采用时频分析的方法,短时傅里叶变换是时频分析中最常用的一种,其思想是将信号划分成许多小的时间间隔,再在每个时间间隔内做傅里叶分析,以确定在该时间间隔内存在的频率[4]。
DSTFT的基本形式可定义为:
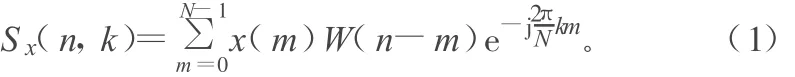
具体做法就是用一个窗函数乘时间信号,该窗函数的时宽足够窄,使窗内的信号可以看成是平稳的,然后进行傅里叶变换,得到信号的瞬时频率。如果让窗函数沿时间轴移动,就可得到信号频谱随时间变化的规律。其中W(n)为所选的分析窗函数,窗口长度为N。由式(1)可以看出DSTFT将时域和频域组合在一起,反映了所考察时间点附近的频率分布情况,因而可以提取频率局部信息。
采用DSTFT方法对PCM/FM信号进行解调时,虽然信号的采样率fs和码速率Rb是已知的,但是由于存在的多普勒频移未知,因此需要较精确地估计信号对应“0”码和“1”码内的频率,下面介绍利用DSTFT估计信号频率的方法。
因为信号 x(n)在长连“0”码或长连“1”码内,此时信号具有单一频率f,根据式(1)给出的DSTFT的定义,设定频率的搜索范围,搜索频率步进为Δf,对信号 x(n)做DSTFT得:
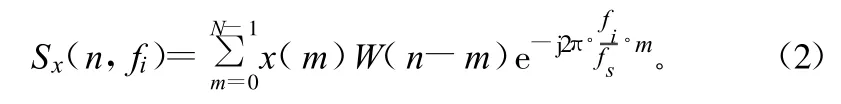
式中,fi=f-fd+(i-1)Δfi;N为搜索频率时的窗口宽度。根据式(2)可以计算出在一定频率范围内信号x(n)在不同频点的频谱幅值,搜索Sx(n,fi)的最大值,则Sx(n,fi)的最大值对应的fi即为信号x(n)对应的频率。
通过以上分析可知:采用DSTFT解调PCM/FM信号是在一定频段内通过逐频点搜索进行测频与多普勒频偏修正,因此测频的精度与数据长度和频率搜索的步进有关。若要提高测频精度就要增加做DSTFT数据的长度,即寻找更长的连“0”和连“1”。
需要强调的是,DSTFT解调PCM/FM信号的先决条件是:窗函数内的数据必须在一段长连“0”或长连“1”码内,当数据不满足这一条件时,频率测量将产生很大误差,导致解调时误码率的升高。这对数据的要求较为苛刻,不利于实际的信号解调。为了解决这一问题,下面讨论一种利用一个码元内数据实现较高测频精度的方法。
2 基于线性预测的多普勒频率估计方法
线性预测是现代谱估计中一种扩展数据的方法,旨在在有限的数据长度内尽可能地改善谱估计的分辨率。借鉴这一做法,采用DSTFT解调PCM/FM信号时可以首先选取单个“0”码或“1”码内的数据,然后基于这段数据确定谱估计中AR模型的系数,再通过对数据进行线性预测完成扩展,最后对扩展后的数据进行傅里叶分析。这样即使选取的原始数据很短,通过合理的预测和扩展后也能得到更多的数据信息,有利于测频精度的提高。
这里采用Burg法确定AR模型系数,采用线性预测的方法进行数据外推,具体过程如下[5]:假设数据x(n)在n时刻之前的p个数据{x(n-p),x(np+1),…,x(n-1)}已知,则可以利用这 p个数据来预测n时刻的数值x(n)。记^x(n)是对真实值x(n)的预测,则:
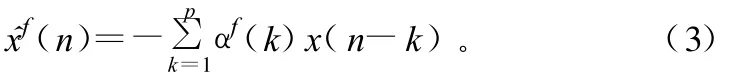
式中,f表示前向预测(forward prediction)。

式中,b表示后向预测(backward prediction),且数据长度p与AR模型的阶数相同。
令X(n)表示外推后的数据,则根据式(3)和式(4)可得:

得到X(n)后再通过DFT即可对这段时间内的数据进行频率估计。
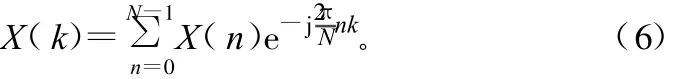
由以上分析可知,原始数据x(n)经过外推后使信号扩展,相当于增加了时域有效数据的长度,提高了频域分辨率。
3 性能与仿真结果分析
由DFT的有关定义可知当数据长度N增加时,频率分辨率将会提高。在此对基于线性预测的多普勒频率估计方法进行了仿真实验,仿真条件为:信号的采样率 fs为20 MHz,码速率Rb为2 MHz,载波频率fc为2.4 MHz,调制系数为0.35 Rb,fd表示多普勒频率,FFT长度为2 048,蒙特卡罗实验次数为1 000次。
多普勒频率fd=65.3 kHz,AR模型阶数(假设原始数据长度与AR模型阶数相同)分别为8、10和12,外推数据长度为前后向各外推500点时,信号在不同SNR条件下测频误差的仿真结果如图1所示。
由图1可以看出:当原始数据长度相同时,利用扩展后的数据进行多普勒频率估计的精度明显高于利用原始数据直接估计的精度。同时,外推数据点数相同时,AR模型阶数越大,频率测量的误差越小。
AR模型阶数为10阶、外推数据长度分别为前后向各外推500、1 000和1 500点时,信号在不同SNR条件下测频误差的仿真结果如图2所示。

图1 AR模型阶数不同对测频精度的影响

图2 外推的数据长度不同对测频精度的影响
由图2可以看出:当AR模型阶数相同时,外推的数据越长,频率测量误差越小。
AR模型阶数为10阶、外推数据长度为前后向各外推500点时,信号在不同多普勒频偏条件下测频误差的仿真结果如图3所示。
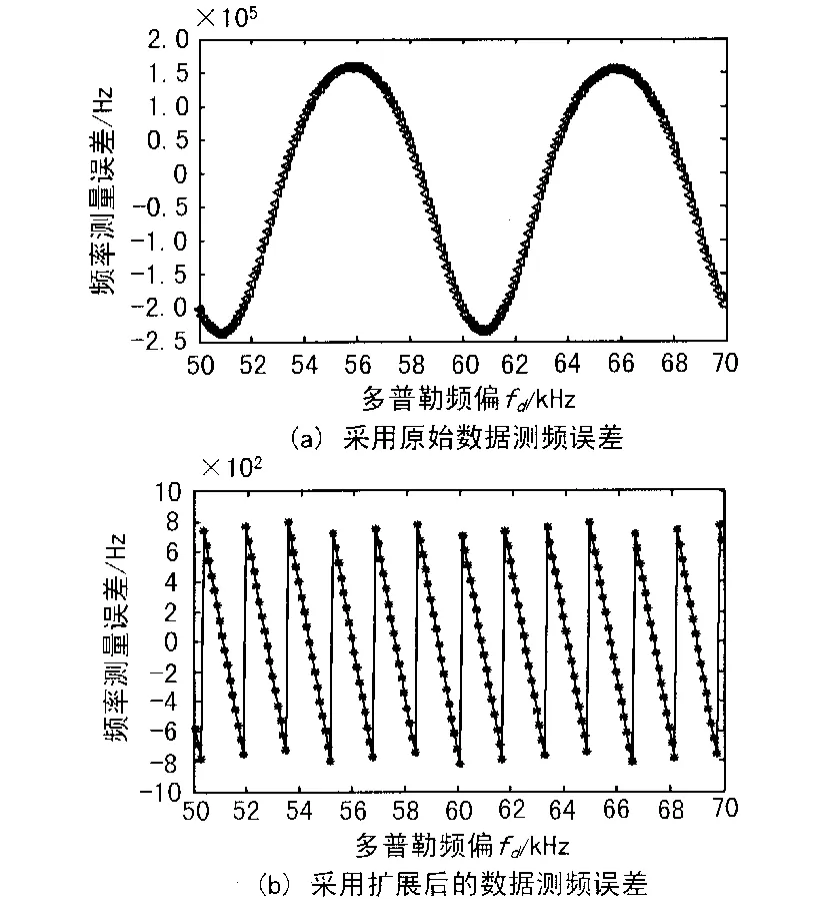
图3 多普勒频率fd不同对测频精度的影响
由图3可以看出:当多普勒频率预设值位于FFT输出2点中间时,频率估计的误差最大,位于基频整数倍时估计误差最小,并且在相同FFT长度下,扩展后的数据做FFT的频率分辨率显著提高。
下面比较采用DSTFT与线性预测2种方法测量多普勒频偏的运算量,信号条件与仿真条件相同。其中,采用DSTFT进行多普勒频率估计时,假设所需的码元数为5,频域搜索步进为1 kHz,多普勒频率fd=±100 kHz,则每个码元中的采样点数n=fs/Rb=10,搜索频点数m=2fd/1 kHz=200。采用线性预测进行多普勒频率估计时,假设前后向分别外推507点,则初始码元数n=fs/Rb=10,扩展后的数据长度m=1 024点。根据DSTFT和线性预测的推导过程可得到2种方法的运算量如表1所示。

表1 两种方法的运算量比较
由表1可知,在相同的仿真条件下,线性预测测量多普勒频率的运算量略小于DSTFT测频的运算量,并且线性预测能够在一个码元内完成频率测量,不需要搜索长连“0”码和长连“1”码,因此降低了对数据的要求,提高了实时处理的能力。
4 结束语
软件解调PCM/FM信号常采用DSTFT方法,DSTFT是一种开环的解调方法,由于没有跟踪环路,能够大大提高解调速度。采用DSTFT解调时通常在长连“0”码和长连“1”码内通过逐个频点搜索的方法进行多普勒频率估计与修正,这种方法估计的精度和运算量成正比,且对数据要求较高,因此不利于软件解调的实现。这里针对这一缺点提出了基于线性预测的多普勒频率估计方法,通过对单个“0”码或“1”内的数据进行线性预测,完成数据的扩展,再通过FFT估计出多普勒频率,这种方法能够用较少的数据进行较高精度的多普勒频率估计,在不影响数据时间分辨率的前提下提高了频率分辨率。
[1]郑立岗.PCM/FM遥测系统中用于去除多谱勒频率和载波频偏的新方法[J].信号处理,2004,20(3):10-13.
[2]李秋娜.基于虚拟无线电的PCM/FM信号解调方法[J].系统仿真学报,2007,19(7):22-26.
[3]ZHANG Lang-ying,YUAN Sij-ie,HOU Xiao-min.A Novel PCM/FM Demodulation Method Using DSTFT Analysis[J].9th International Conference on Signal Processing Proceedings,2008(10):1775-1779.
[4]章兰英.PCM/FM遥测信号软件解调算法的研究与实现[D].北京:装备指挥技术学院,2005:28-32.
[5]张贤达.数字信号处理理论、算法与实现[M].北京:清华大学出版社,2005:546-548.

