基于FPGA的高速误码插入技术分析
程翰林
(桂林电子科技大学信息与通信学院,广西桂林541004)
0 引言
数字传输损伤是指信号在数字端到端传输过程中产生的差异。误码是其中的一种重要损伤,对数字网的业务质量和网络工作性能都会产生很大影响。误码损伤模拟单元是数字网传输损伤模拟系统中的关键一环,用以在室内评测通信网对误码损伤的承受能力,测试各个通信设备的技术指标和工作情况,尽早发现和解决问题。
随机误码插入技术是数字网传输损伤模拟系统中的关键技术之一,可通过硬件或软件方法得以实现。随着电子技术的迅猛发展,现场可编程门阵列(FPGA)以其强逻辑功能和高集成度等特点,在各种通信系统中得到了广泛应用。基于FPGA的硬件实现误码插入的设计方案较软件而言具有复杂性低、精度高和快速灵活可移植等优点。
1 误码损伤模拟中存在的问题
近年来,通信技术的发展日新月异,工作频率更高、信号处理速度更快成为通信系统的发展方向。为了适应高速通信系统的测试环境,就需要处理速度更快的数字信道误码损伤模拟产品,模拟高速信号在信道中的误码损伤。国内产品其信号处理速度不够理想,很难跟上现代通信系统的发展。国外某些产品虽然能达到很高的处理速度,但其价格昂贵,而且很多功能根本用不到。因此需要研制基于FPGA的能工作在1 Gbps以上的误码损伤模拟设备,同时应具备模拟高斯噪声下的误码特性,并能对误码率在5×10-3~1×10-10范围分档控制的功能。
2 误码插入技术
按照常规的方法,在一个时钟周期只能对输入数据流的一位插入误码,如图1所示,想要对高速码流进行误码插入操作,只能通过提高时钟频率得以实现。
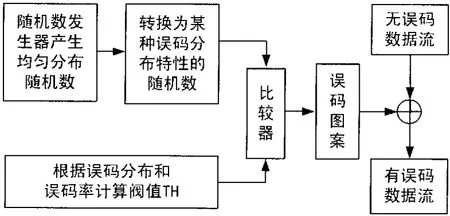
图1 随机误码插入原理图
一方面,时钟频率过高会大大降低电路可靠性,如果打算运行在千兆赫兹时钟频率下,当信号速率高达上GHz时,每比特的宽度要小于1 ns。若门阵列时延、传输线时延以及各种运算时延叠加在一起,使总传输时延超过时钟周期,就会影响运算结果,产生错误的误码图案。另一方面,时钟频率的提高会使功耗明显增加。因此,由FPGA构成的误码损伤模拟单元不可能只靠提高时钟频率达到Gbps的工作速度。
这就需要对传统的方案进行改进,采用并行方式,在一个时钟周期内,同时对输入数据流的多位进行并行加误码处理,如图2所示。采用这种方案,可以将工作时钟频率降低到串行处理时的1/8,也就是说要达到1 GHz的处理速度,只需125 MHz的时钟驱动即可。

图2 8路并行高速误码插入原理图
特别注意的是系统的误码图案应保持不变,这样才能使等效性得到保障。在图2中可以看到,输入的无误码数据流经过串并变换分为8路,同时利用伪随机序列自身特性,在每个时钟脉冲产生8路相互关联的低速伪随机码,经过后续处理形成误码图案,对变换后的各路输入码流分别进行误码插入处理,最后再通过并串变换合成一路数据流输出。比较图2和图1不难发现,保证等效性的关键在于保证在一个时刻下并行8路产生的均匀分布随机数和在8个连续时刻下原始1路产生的均匀分布随机数的数值完全相同。
3 高速误码插入实现
信号在信道中传输产生误码损伤,通常用误码分布和误码率2个特征来描述。因此,误码插入就必须解决误码分布的产生和误码数量的控制问题。按照上述讨论的方案,由随机数发生器根据要模拟的误码特性产生某种分布的随机数序列,以解决误码分布的问题,待分布确定后,通过相应的阀值即可实现对误码数量的控制。
3.1 随机数的产生
由硬件或软件的方法产生的随机数都不是绝对的随机数,而是相对的,称为“伪随机数”。在FPGA内利用线性反馈移位寄存器(LFSR)结构实现伪随机数发生器的方法,所产生的伪随机序列周期长,随机特性好,而且结构简单,易于实现。
产生具有误码分布特性的随机数有多种方法,其中便于FPGA实现的是利用LFSR产生均匀分布随机数序列,随后将其通过某种变换获得特定分布的随机数序列。
3.1.1 均匀随机数生成
图3是m级LFSR的电路结构(这里采用m=31反馈系数20000000011(八进制)的逻辑结构)。
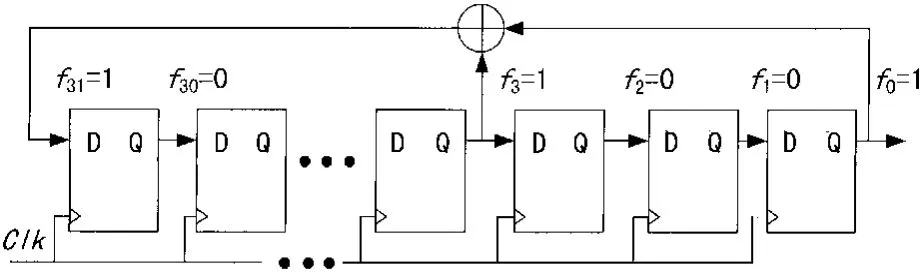
图3 m=31的一种反馈逻辑结构
其中fi为反馈系数,值为1表示参与反馈,为0则表示反馈线断开。⊕表示模二加运算。显然,LFSR的输出序列是有周期性的。因为一旦m个寄存器上出现了以前经历过的状态,则以后的状态将周而复始。LFSR的周期 r≤2m-1。LFSR的周期只与反馈系数有关,选取特定的反馈系数可使周期达到最大值2m-1,这时LFSR所产生的伪随机序列称为最长线性移位寄存器序列(或称m序列)。随着m的增大,LFSR消耗的FPGA内部逻辑资源量呈线性增加,而LFSR输出序列的周期却呈指数增长,这一点对实际应用来说是十分有利的。
用此结构串行输出可产生周期为231-1的伪随机序列A0,A1,A2…,如果把31个移位寄存器同时作为输出,则产生一个31位的在1~2 147 483 647之间的伪随机数。
根据移位寄存器的逻辑关系可知:
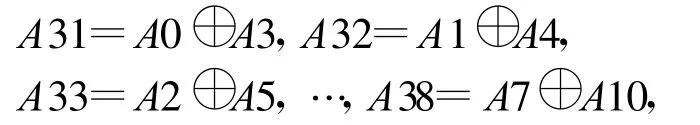
于是便可根据后续码元与前面码元的这些关系设计出电路,即可得到并行输出多路随机数的等效电路。在系统初始化时对寄存器付初值A0~A30,然后根据逻辑关系得出 A31~A38,最后重新组合 A0~A38,把 A0~ A30,A1~A31,…,A7~ A37作为 8路的伪随机数并行输出,而A8~A38则送回组合逻辑去产生下一时刻的数据,如图4所示,以此循环下去即可产生等效的8路相关联的均匀伪随机数。
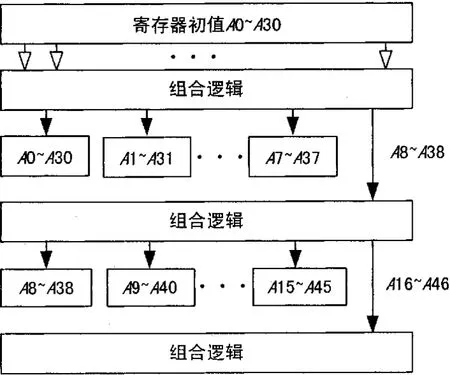
图4 并行多路伪随机数产生过程
3.1.2 高斯随机数生成
这里希望模拟高斯白噪声下的误码特性,因此需要构造高斯分布的随机数序列,可由均匀分布的随机数来产生。
高斯分布随机数如果精度不够,不能有效模拟高斯噪声环境;而精度过高又会消耗大量资源,况且本系统对误码的模拟当中本身存在近似处理,因此对高斯分布的精度要求并不高。这里采用折中处理,选择近似抽样中基于中心极限定理的硬件实现,方法简单且精度适中,可用来产生高斯分布随机数。根据中心极限定理,多个相互独立的均匀分布之和服从高斯分布。这里采用20路均匀分布数之和来产生服从高斯分布的定点数据。设计时,将20路均匀分布随机数发生器赋予不同的初值,可以保证各路数据的相互独立性。
3.2 产生误码图案
误码分布确定后,接下来需要解决误码数量的控制问题,即根据需要的误码率计算出相应的阀值TH。误码率Pe、误码分布的概率密度函数 f(x)以及阈值TH的关系满足式(1)。由式(1)可以计算出阈值TH:
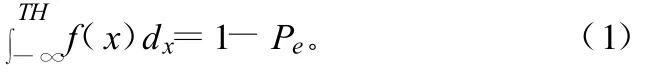
当某个指定的误码率所对应的阀值确定后,8路均采用相同的阀值参与运算,将之前产生的各路随机数R分别与阈值TH做比较,若R>TH,则输出1,否则输出0,从而由0、1组成了各路误码图案数据流。由于之前随机数产生电路保证了等效性,使得此时的误码图案与常规串行处理时保持不变。
将各路误码图案数据流分别与各自输入数据流按位做模二和运算,便完成了各路随机误码插入。最后经过并串变换,组合成一路输出误码数据流。
4 性能测试
将设备与高速误码仪相连,搭建测试环境。误码损伤模拟单元可提供5×10-3~1×10-10可调的8种随机误比特率模式,设备的主控板通过RS232接口与配置计算机相连,接收配置计算机发送的信道仿真参数及其他控制命令。测试时利用配置计算机提供的用户界面,输入误比特率等参数,完成模拟器仿真参数配置。误码仪提供1 Gbps的高速码流作为输入信号,FPGA根据接收到的设置参数进行随机误码插入处理,并将处理后的码流送回误码仪中进行测试,在误码仪中显示测试报告。设备工作正常,测试结果如表1所示。
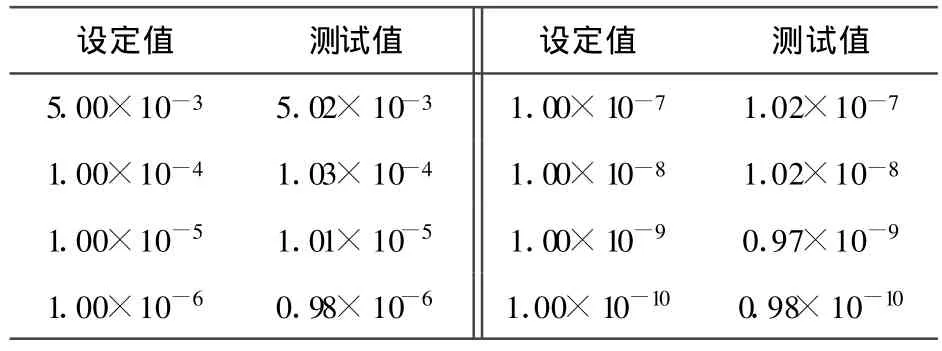
表1 误码测试结果
5 测试结果分析
由以上测试结果可知,所设计的误码损伤模拟单元达到了工程上要求的功能目标和性能指标。该设计无论从处理速度还是误码率的控制上都达到了实用要求,可用于系统联调中模拟误码损伤环境,测试通信网中设备在各种误码环境中的工作情况,以发现问题和不足。
该设计在阀值计算时应用了Matlab软件,以提高精度,计算的 TH阀值直接写入了代码中。采用了Altera公司的StratixII系列芯片,此单元消耗了总资源的2%,留下了充足的资源做其他功能的扩展之用。以8路并行处理方式,实现了处理1 Gbps的码流。如需处理更高速率的码流,可通过扩展更多路数实现,但同时需要消耗FPGA更多的资源。该设计可扩展性好,可以非常方便地在FPGA中实现,对类似的并行处理电路也有一定的借鉴意义。
6 结束语
在分析数字信道传输损伤模拟中误码插入速度和效率等问题的基础上,用多路并行处理的方法成功地解决了传统方式在速度上的局限性,测试结果达到了指标要求。该设计在保证等效性的前提下,可靠易行,灵活可移植,有效提高了误码插入效率,为数字传输损伤模拟中高速插入随机误码提供了一种可行方案。
[1]ROBERT M.Fast Bit Error Generation for the Simulation of MPEG-2 Transmissions in Wireless Systems[J].IEEE-W ireless Communications and Networking Conference,1999,9(1):324-328.
[2]LEE D,LUK W.A Hardware Gaussian Noise Generator Using the Wallace Method[J].IEEE Transactions on Very Large Integration(VLSI)Systems,2005,13(8):911-920.
[3]张胡平,姚远程,冯 立.数字信道模拟器中随机误码插入的设计和实现[J].西南科技大学学报,2008,9(3):67-70.
[4]束礼宝,宋克柱,王砚方.伪随机数发生器的FPGA实现与研究[J].电路与系统学报,2003,6(3):121-124.
[5]刘 宇.基于FPGA的并行PRBS序列的实现[J].国外电子测量技,2008,5(5):6-8.
[6]丁 群.对高速M序列产生电路的探讨[J].电气电子教学学报,2000,20(1):30-31.

