基于卡尔曼滤波的RAIM方案研究

周富相,郑晓晶

(总参通信训练基地,河北宣化075100)

0 引言

卫星导航系统除了提供导航功能外,还必须具有在系统不能使用时及时向用户发出告警的能力,这种能力叫做系统的完好性[1]。当卫星导航用于航空等生命相关场合时,完好性成为决定性指标。因此,卫星导航系统的完好性问题已成为卫星导航领域重点解决的问题,并将存在于卫星导航整个生命周期。

引起接收机伪距偏差的主要因素有较大的卫星钟漂、各种欺骗与干扰以及卫星组成部分的故障等,这里统称为卫星故障,在GPS系统中这种故障发生的概率大约为10-4/h[2]。对这种故障,导航系统本身做出告警反应的时间较长,如GPS系统的反应时间为15 min到数小时[3],对于生命相关场合显然太慢,不能满足需求。因而出现了接收机自主完好性检测技术[4](Receiver Autonomous Integrity Monitoring,RAIM)。

1 基于卡尔曼滤波的RAIM方案

为了使导航接收机自主完好性检测算法与卡尔曼滤波位置解算结合起来,有效降低接收机自主完好性检测的漏检率和误警率(文献[5]对漏检率和误警率作了定义),提出了基于卡尔曼滤波的RAIM检测方案,并对方案进行了仿真分析。

1.1 离散的卡尔曼滤波方程

卡尔曼滤波是一种线性最小方差估计,估计值是观测值的线性函数[6],它的估计准则是估计误差方差最小且无偏。在计算方法上采用了递推形式,使计算量减小,并且使用状态空间法在时域内设计滤波器,所以适用于多维随机过程的估计。

对导航系统,有

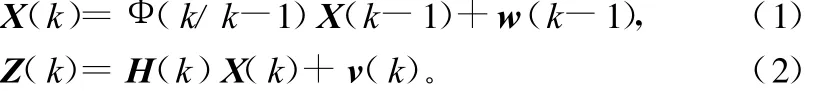
式中:X(k)是k时刻的n维状态矢量,也是被估计矢量;Z(k)是k时刻的m维观测矢量;Φ(k/k-1)是k-1时刻至k时刻的一步状态转移阵,且有

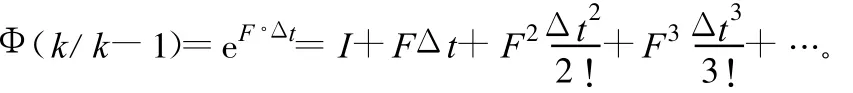
式中,F为描述目标运动的动态模型;w(k-1)为k-1时刻的系统噪声序列;H(k)为k时刻的观测矩阵;v(k)为k时刻的观测噪声序列;w(k)和v(k)为互不相关的零均值的白噪声序列,并有

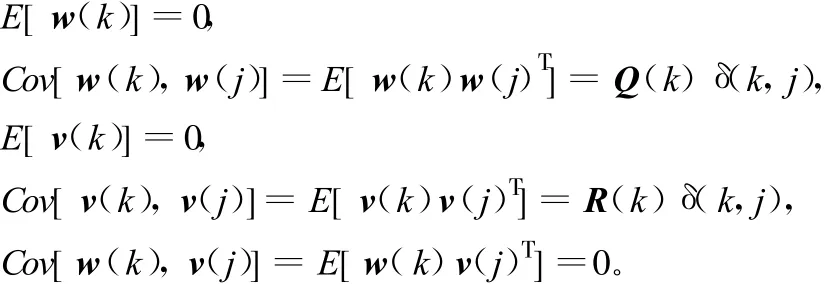
式中,E[·]表示取均值;Cov[·]表示取协方差;Q(k)为系统噪声序列的方差阵;R(k)为测量噪声序列的方差阵,它们分别为已知的负定阵和正定阵;δ(k,j)为 Kronecker δ函数 。

系统初始状态的一二阶统计特性为:

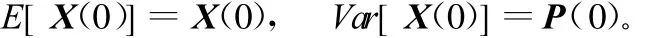
式中,Var[·]表示方差。卡尔曼滤波器要求X(0)和P(0)为已知量,且X(0)与 w(k)以及 v(k)都不相关。具有完好性检测的卡尔曼滤波流程图如图1所示,流程图显示了完好性检测在整个卡尔曼滤波过程中的位置。

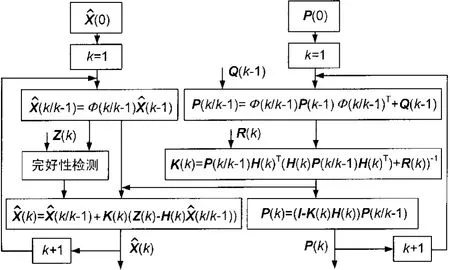
图1 具有完好性检测的卡尔曼滤波流程

在以上的假设条件下,有离散的卡尔曼滤波方程如式(3)～式(7)所示:

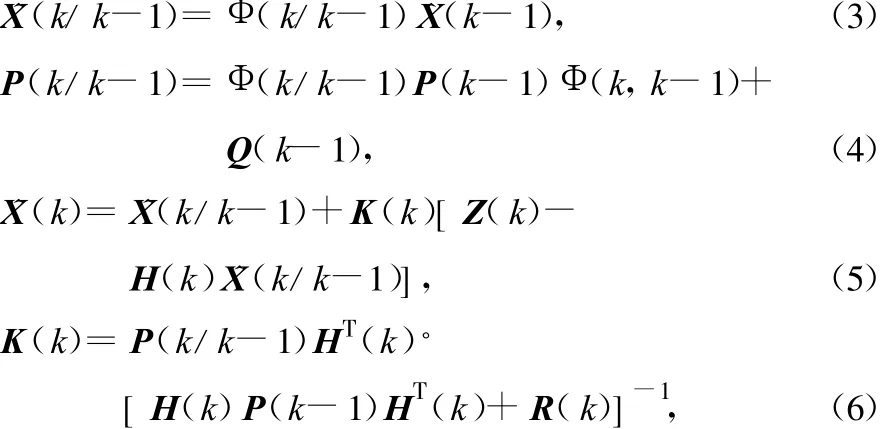
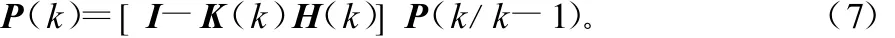
式(3)、式(4)称为时间修正方程;式(5)～式(7)称为测量修正方程。只要给定初值 ^X(0)和P(0),根据k时刻的测量值Z(k),就可通过递推计算得到k时刻的状态估计^X(k),这里k=1,2,3…。

1.2 基于卡尔曼滤波的多故障检测

如果将式(1)和式(2)作为导航接收机系统的状态模型和测量模型,那么,卡尔曼滤波器完成一次时间更新后,观测量 Z(k)与预测观测量 H(k)^X(k/k-1)之间的残差为:

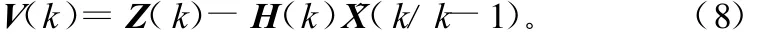
当无异常时卡尔曼滤波器的残差 V(k)是零均值高斯白噪声,而其协方差阵为:

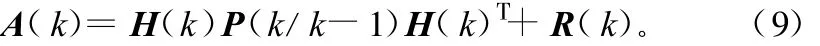
作二元假设:

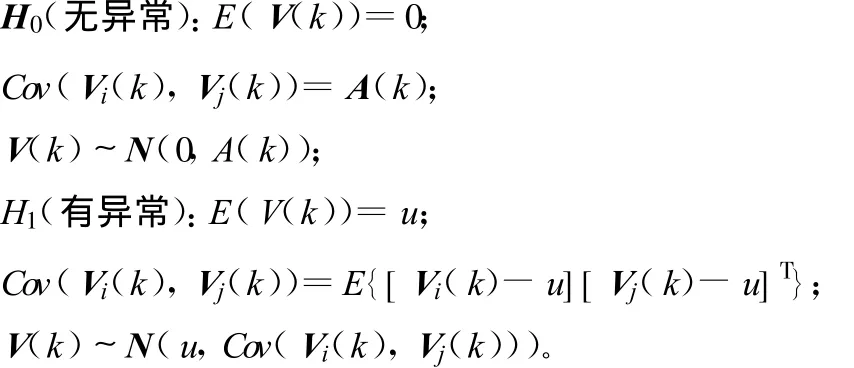
检测统计量构造为:

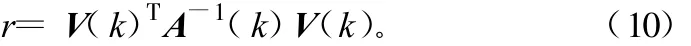
根据统计分布理论[7],当无异常时r服从自由度为m的χ2分布,m为可视卫星数目。设误警率为PFA,那么检测限值Td由下式确定[8]:

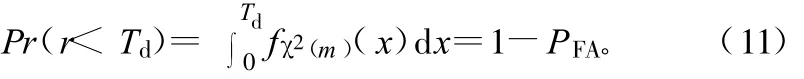
当r＜Td时,系统正常工作,测量伪距没有异常;当r＞Td时,系统有异常,需要对伪距信息进行检测。

当系统有故障或发生其他异常情况时,根据统计分布理论,检测统计量r服从非中心化参数θ=E(r)的 χ2分布,自由度为 m。如果漏检率用PMD表示,则漏检率PMD用下式确定[8]:

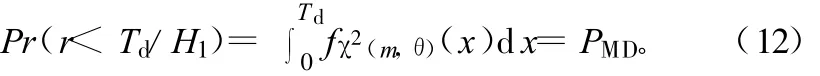
完好性检测算法流程图如图2所示,由故障检测和故障识别2部分组成。故障检测部分首先计算出检测统计量 r,然后与检测门限值 Td进行比较,从而判断出系统是否有故障或发生其他异常情况。如果有故障或异常情况,进入故障识别阶段。

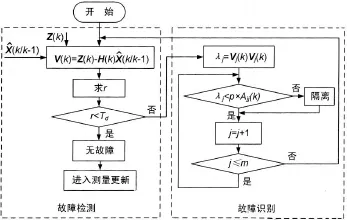
图2 完好性检测流程

1.3 故障识别

设观测量Z(k)和预测观测量 H(k)^X(k/k-1)之间残差 V(k)的各元素平方为 λj=Vj(k)·Vj(k),根据式(9)可得到 V(k)方差的对角线元素Ajj(k)。为了有效降低接收机自主完好性检测的漏检率和误警率,引入故障检测调整系数p(p≥1),逐个比较 λj与p×Ajj(k),如果 λj大于p×Ajj(k),则表明第j个观测伪距有异常,并将其隔离。故障检测调整系数 p的取值可以通过大量的实测数据来确定,当p的取值大于1时,会同时降低检测的漏检率和误警率。

完好性检测部分所用到的数据来自卡尔曼滤波迭代中的一些中间结果,所要完成的计算只是各伪距残差平方 λj=Vj(k)Vj(k)及检测统计量 r=V(k)TA-1(k)V(k)的计算。计算量并不大,对后续滤波进程的影响不大。从软件实现上看,只在上述计算的基础上再做m(m是可视卫星数)次循环判断。

2 方案仿真

为了验证基于卡尔曼滤波位置解算的RAIM方案对故障检测与识别的性能,利用STK5.0软件产生星座数据,采用MATLAB软件对该方案进行仿真。由于GPS系统已有较为准确的误差统计数据,因此仿真采用的卫星星座是GPS卫星星座。利用了在GPS系统时间1 Jan 2010 13:15:00.00至1 Jan 2010 13:17:00.00之间,在北京地区所有的可视卫星,它们分别是GPS 星座系统第 1、2、3、6、9 、11、15、20 颗卫星。仿真条件如下:故障检测误警率为0.000 000 1,根据式(11)计算得到故障检测门限值为5.950 2 m。设观测噪声均值为0,标准差为5 m。在观测时段内第30 s时刻,对其中一颗卫星对应的伪距加入50 m突变,模拟此时卫星出现故障,相应的伪距出现异常。仿真结果如图3、图4和图5所示。

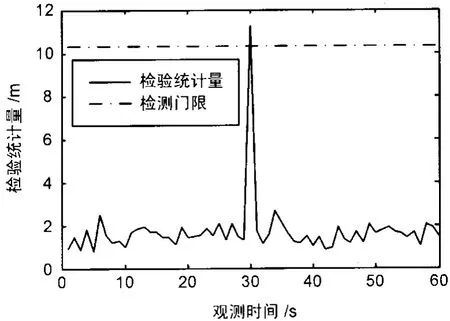
图3 故障检测

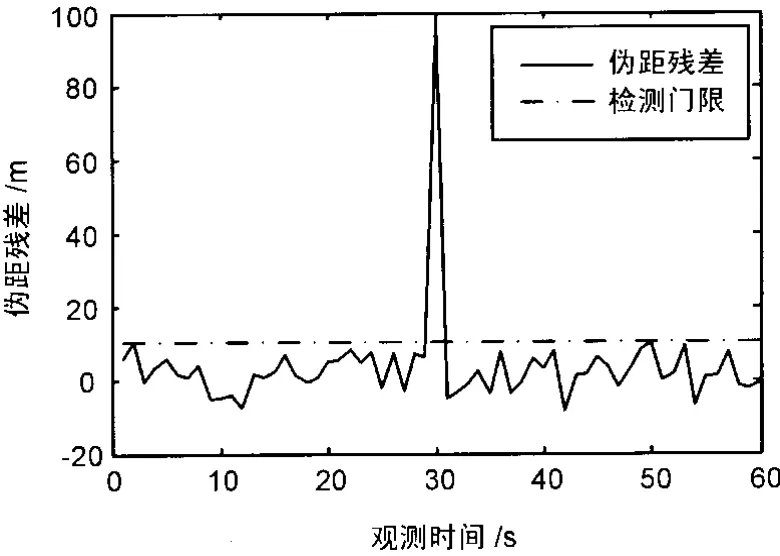
图4 伪距异常检测

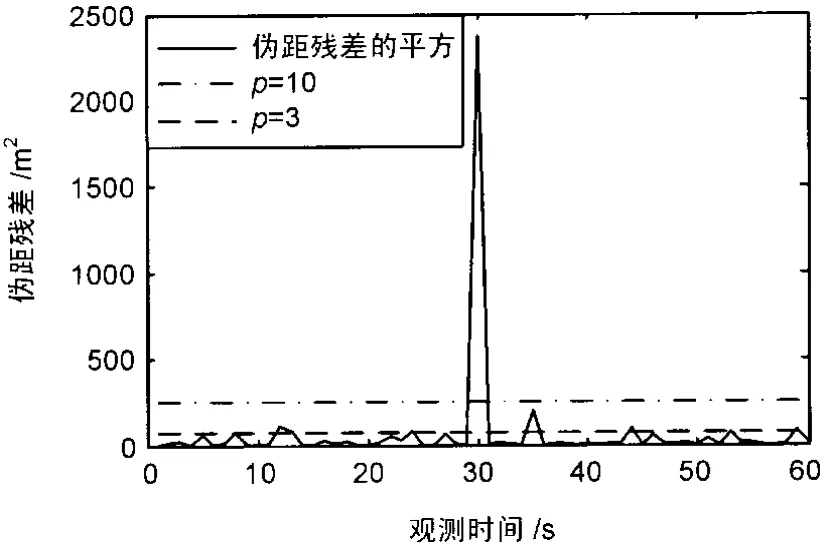
图5 故障识别

从图3和图4上可以看出,在30 s时刻观测伪距发生异常时,相应的伪距残差出现突变,从而导致了检验统计量的突变,检验统计量在30 s时刻超过了故障检测门限值,因此,此时的故障完全能够被检测出来。图5显示了伪距残差的平方和调整系数p分别取10和3时伪距方差的调整值。显然,当调整系数p取10时,能够识别出故障卫星而不会引起误警;当调整系数 p取3时,就存在误警情况。因此,调整系数p的引入有效地降低了系统的误警率和漏检率。以上仿真结果表明,所提出的基于卡尔曼滤波的接收机自主完好性检测方案可行、有效。

3 结束语

完好的系统故障检测性能、快速的故障反馈能力是现代卫星导航定位系统接收机自主完好性检测的发展趋势。所提出的基于卡尔曼滤波的接收机自主完好性检测方案具有告警时问短、运算量小的特点,而且能够有效降低完好性检测的漏检率和误警率。接收机位置解算如果采用卡尔曼滤波法,就可以很容易地将该方案嵌入其中。我国二代卫星导航定位系统正在建设当中,建议在系统建设中考虑好系统的完好性检测扩展能力,在接收机的设计中加入自主完好性检测功能。

[1]BROWN R G.GlobalPositioningSystem Theoryand Applications[M].American:American Institute of Aeronautics and Astronantics,1996:143-164.

[2]XIEG,PULLEN S,LUO M,et al.Integrity Design and Updated Test Results for the Stanford LAAS Integrity Monitor Testbed[C].Albuquerque,NM:Proceedings of ION 57th Annual Meeting and CIGTF 20th Biennial Guidance Test Symposium,2001:681-693.

[3]冯庆堂,沈林成,常文森.一种监测GPS完好性的新方法[J].导航与控制,2004,3(1):4-5.

[4]PAR KINSON B W,AXELRAD P.Autonomous GPS Integrity Monitoring Using the Pseudorange Residual[J].Journal of The Institute of Navigation,1988,35(2):456-460.

[5]杨 婷,黄智刚,李 锐.基于RAIM的多卫星导航系统完好性风险技术研究[J].遥测遥控,2009,30(6):16-18.

[6]秦永元.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998.

[7]盛 骤.概率论与数理统计[M].北京:高等教育出版社,1989.

[8]RYAN S Y.Fault Detection and Exclusion Using Normalized Solution Separation Residual Monitoring Methods[C].Portland.Institute of NavigationProceedingsof ION GPS,2002:565-578.