改进背景值的非等间距GM(1,1)模型

童新安,郭石磊,茹强喜

(洛阳理工学院 数理部，河南 洛阳 471023)

作为灰色系统理论重要理论之一的GM(1,1)模型，已被广泛应用于工业、农业、社会、经济等诸多领域[1-2]。从灰色系统理论建立起，基于等间距序列产生的等间距GM(1,1)模型已经取得了丰富的研究成果.然而，实际工作中得到的往往是非等间距的序列，因此对非等间距GM(1,1)模型的研究具有广泛的现实意义[3-5]。

1 非等间距GM(1,1)模型背景值的改进

1.1非等间距GM(1,1)模型建模机理

非等间距GM(1,1)模型的建模机理如下：

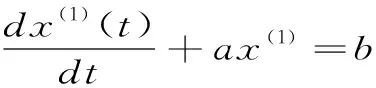
(1)

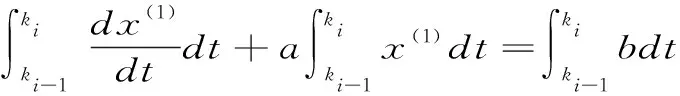
(2)

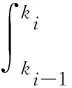
(3)

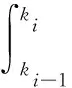
(4)

展开得其矩阵形式为：Y=B×[ab]

(5)

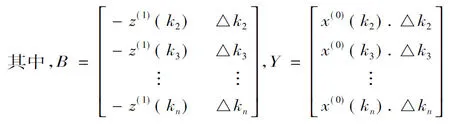
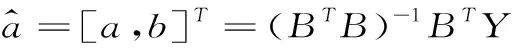
(6)

(7)

4) 对(7)式进行累减还原，得到原始数据的模拟值为：

(8)

1.2非等间距GM(1,1)模型背景值的改进机理

由(7)式可知，GM(1,1)模型的精度主要取决于参数a和b；而由(4)式可见，参数a和b的得到则依赖于背景值z(1)(ki)的构造形式。因此，背景值z(1)(ki)成为直接影响非等间距GM(1,1)模型精度和适应性的关键因素。

分析(7)式中x(1)(t)的解的形式可知，x(0)(ki)△ki+az(1)(ki)=b△ki的解满足非齐次的指数形式，故可将x(1)(t)用如下的非齐次指数函数近似：

x(1)(t)=G·edt+c

(9)

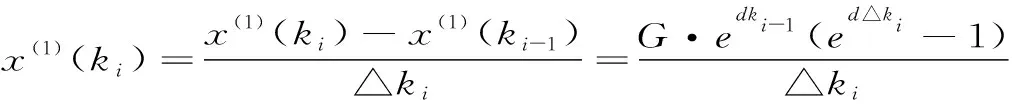
(10)

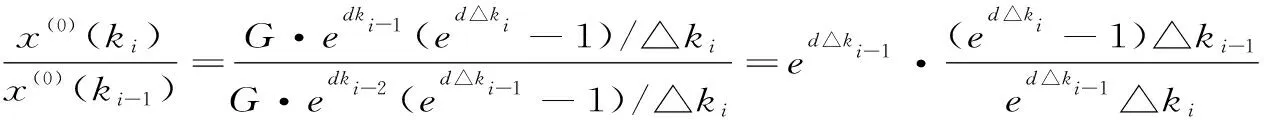
(11)

(12)

(13)

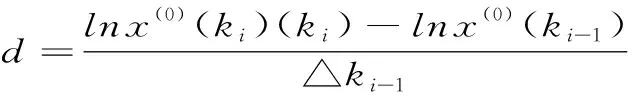
(14)

(15)

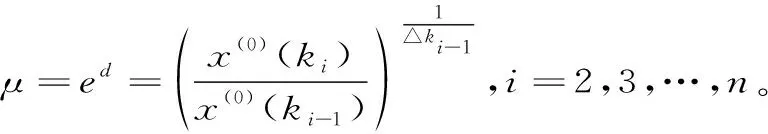
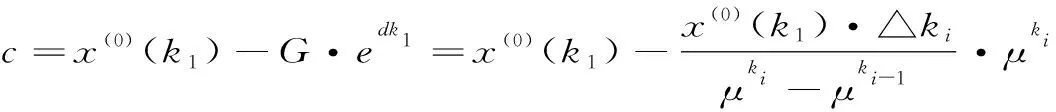
(16)

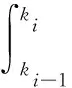
(17)

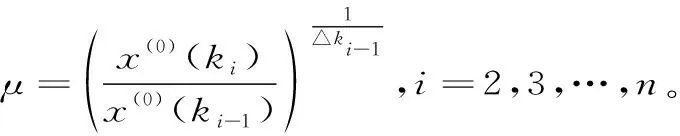
这样，就构造出一种基于非齐次指数函数形式的新的背景值。将(17)式代回(4)式，进而(4)式则可以利用最小二乘法求解，从而得到一种改进背景值的非等间距GM(1,1)模型。

2 应用实例

文献[14]采用了齐次指数函数形式对背景值进行构造，为了便于比较，仍采用文献[14]的算例，对原始数据建立改进背景值的非等间距GM(1,1)模型，并加以比较。

P.G.福雷斯研究了许多材料的长寿命对称循环下温度对疲劳强度的影响，我们从所给试验曲线中采集到钛合金强度随温度变化的数据如下表1所示：

表1 钛合金强度随温度变化关系

按照本文建立起来的模型为：

还原式为：

所建模型与文献[14]所建模型的相对误差如下表2所示：

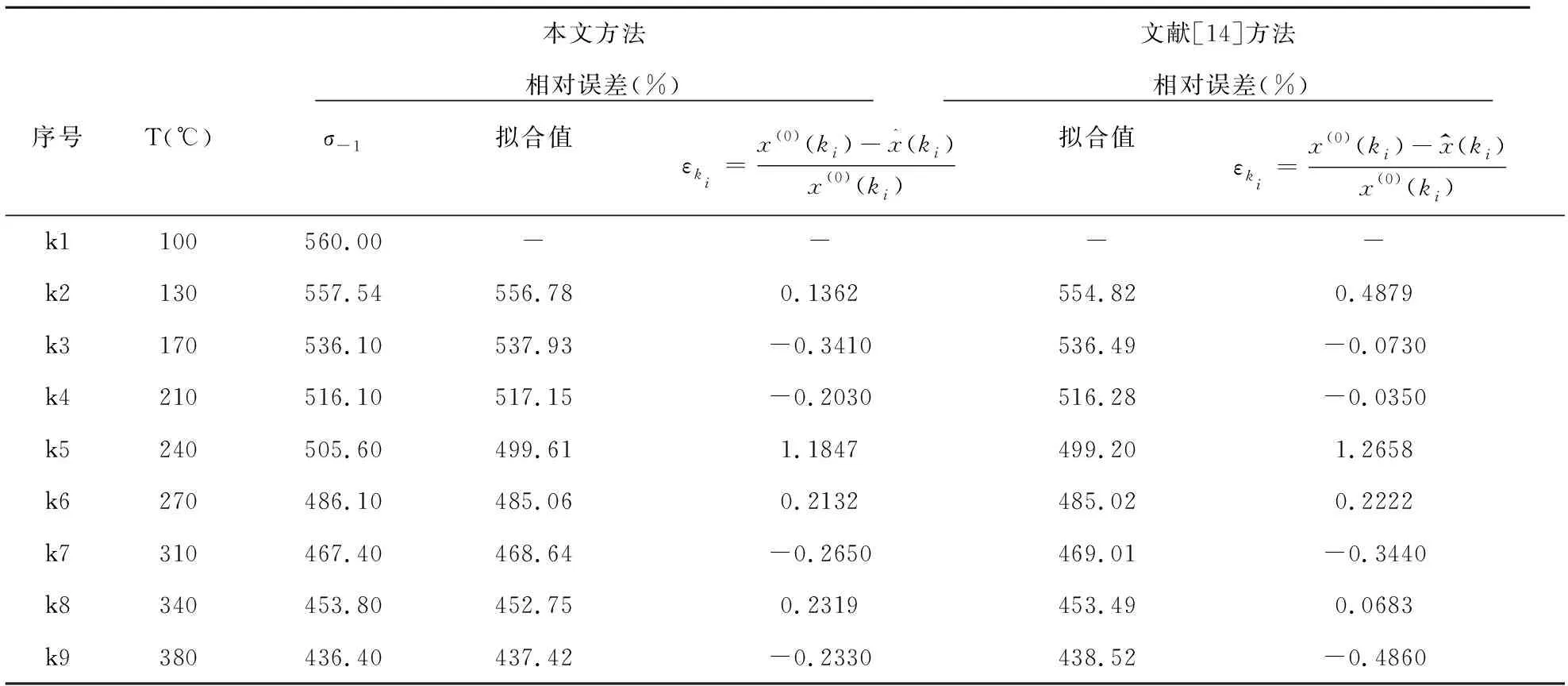
表2 模型精度对比表

3 结语

灰色系统建模理论中，背景值是影响非等间距GM(1,1)模型建模精度的重要因素之一。本文为了提高模型精度，对背景值的表现形式进行了研究，通过非齐次指数函数来拟合一次累加生成序列，提出了一种改进的背景值构造方法。并应用改进背景值的非等间距GM(1,1)模型对钛合金疲劳强度随温度变化的关系进行了建模，取得了满意的效果，模型精度高达99.9%，建模结果表明了该方法的有效性。

[参考文献]

[1] 刘思峰,谢乃明.灰色系统理论及其应用[M].北京:科学出版社,2008:1-5,95-112.

[2] 肖新平,宋中民,李峰.灰色度技术基础及其应用[M].北京:科学出版社,2005:1-25

[3] 沈建国.灰色GM(1,1)模型的改进及其应用[J].数学的实践与认识,1990(3):10-15.

[4] Deng Julong. A novel GM(1,1) model for non-equalgap series[J].The Journal of Grey System, 1997,9(2):111-116.

[5] 罗佑新,周继荣.非等间距GM(1,1)模型及其在疲劳实验数据处理中和疲劳实验在线检测中的应用[J].机械强度,1999,18(3):60-63.

[6] 戴文战,李俊峰.非等间距GM(1,1)模型建模研究[J].系统工程理论与实践,2005(9):89-93.