两两NQD随机变量列所产生线性过程的完全收敛性
佟 欣,赵冬霞
(大庆师范学院 数学学院,黑龙江 大庆 163712)
0 引言
定义1:称r.v.X和Y是NQD(NegativelyQuadrantDependent)的,若对∀x、y∈R有
P(X 称r.v.列{xn,n≥1}是两两NQP的,若对∀i≠j,Xi与Yj是NQD的。随机变量X与Y是NQD的,当且仅当对于任何单调递增函数f,g均有Cov(f(X),g(Y))<0. 最早对完全收敛性的研究是从独立同分布的实随机变量开始的。由上述定义容易看出两两NQD列是包含两两独立列在内的非常广泛的随机变量列,后来的许多负关联列都是在此基础上衍生出来的。因此,对两两NQD列的研究就显得更为基本,而目前对两两NQD列的研究还不够完善。张立新[1]研究了两两NQD列部分和最大值的一般形式完全收敛的充要条件。本文假设{xn,n≥1}是同分布的随机变量,C为正常数,在不同地方可以表示不同的值。本文研究了更为广泛的一类随机变量列,设{xn,n≥1}满足: (A)存在常数C,对任何一列单调函数{fi;i≥1},若Varfi(X1)<∞,对任意的i成立,则有 于是可以看出满足条件(A)的随机变量列是包含两两NQD列的一类更为广泛的随机变量列。 满足(A)的移动平均过程完全收敛性定理如下: 1)Φ是有界的,并且Φ在a点连续; 2)存在δ>0及C>0,使得对所有|x|≤δ,都有|Φ(x)|≤|x|,则 注:特别取Φ(x)=|x|p,P≥1,由上式可得 引理2[3](缓变函数的性质):当h(x)>0为x→∞时的缓变函数,则 对{ai;-∞ 只需证明 (1) (2) 先来考察(1)式成立((2)式证明与(1)式类似) 易见,对∀ε>0,有An⊂Bn∪Cn,由此只须证明 (3) (4) (5) aniZi为单调非降函数,而{Yi;i≥1}满足条件(A),故有 (6) (7) 综合(5)、(6)、(7)式再由引理1,有(1)式 =C(I1+I2) 由引理1,再利用缓变函数的性质,于是 当1 (8) 由文献[4],对于∀≥1,a>0,有 (9) 利用(8)(9)两式及缓变函数性质和引理可得 选取δ>0,类似可证得:I4<∞ 与I1<∞的方法类似,可证得(3)式成立,于是定理得证。 [参考文献] [1] 张立新,王江峰.两两NQD列的完全收敛性的一个注记[J].高校应用数学学报:A辑,2004,19(2):203-208. [2] Burton R M , Dehling H. Large deviations for some weakly dependent random processes[J]. Statist Probab lett, 1990, 9(9): 397-401. [4] Yu De-ming,Wang Zhi-jiang.Complete of Moving Average Processes under Negative Dependence Assumptions[J]. Mathematical Applicata, 2002, 15(1): 30-40. [5] 汪嘉冈.现代概率基础[M].上海:复旦大学出版社,1986.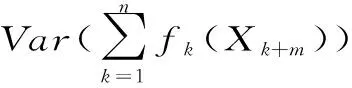
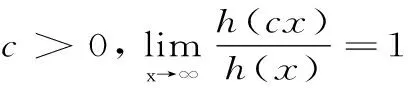
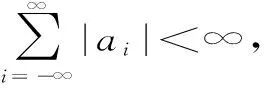
1 几条引理
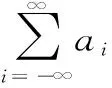
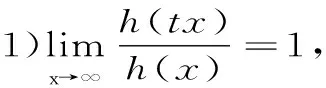
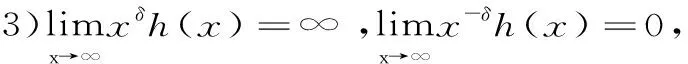
2 定理的证明
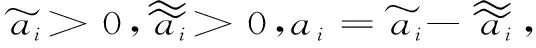
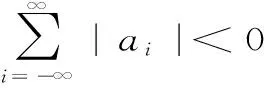
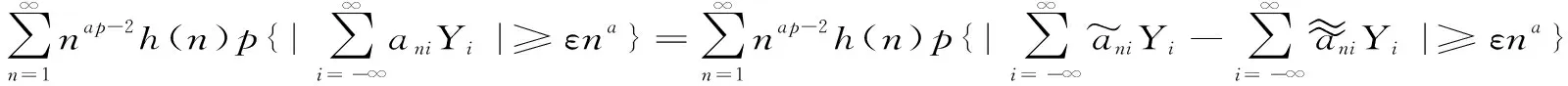
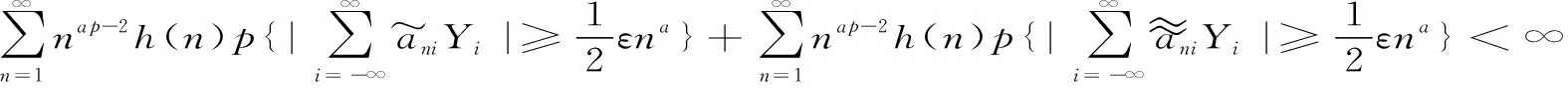
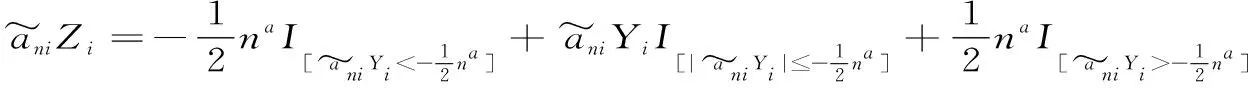
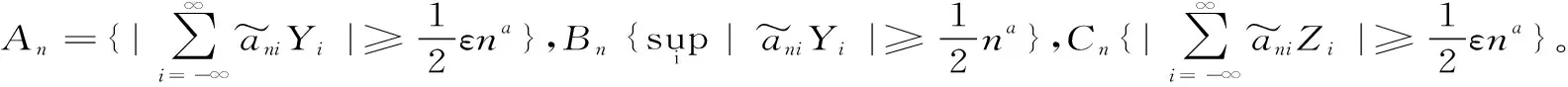
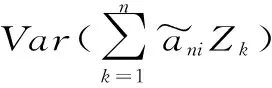
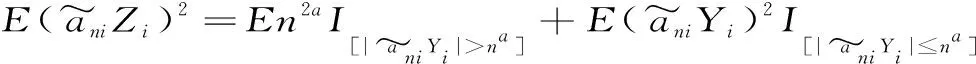
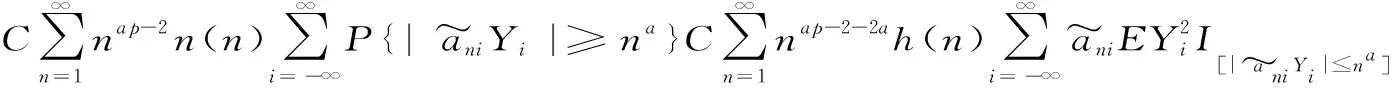
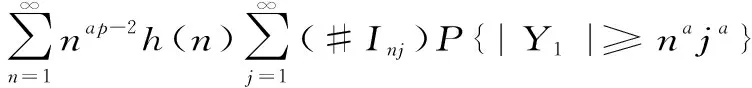


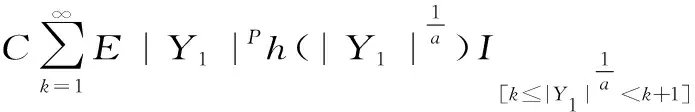
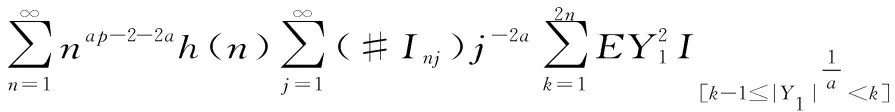


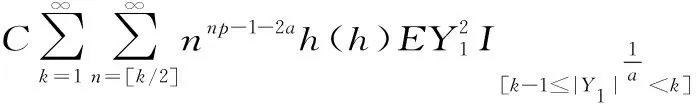
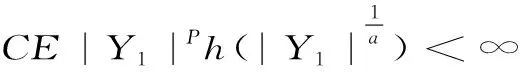
——高大庆作品欣赏

