凸函数定义等价性的进一步探讨
张 金
(宿迁高等师范学校 数学系,江苏 宿迁 223800)
0 引言
凸函数是一重要的概念。 已有的文献中,在给定的区间I上,给出了凸函数多种不同形式的定义,并对定义之间等价性作了分析与证明,见文献[1]~[5]。 下文拟对一般区间I上的凸函数最基本的定义作一概述,进一步探讨与证明它们之间的等价性。
1 凸函数的基本定义
下面给出凸函数几种定义:
定义1 :设函数f(x)在区间I上有定义,f(x)称为I上的凸函数,当且仅当:∀x1,x2∈I,有
(1)
定义2 :设函数f(x)在区间I上有定义,f(x)称为I上的凸函数,当且仅当:∀x1,x2,…,xn∈I,有
(2)
定义3[6]:设函数f(x)在区间I上有定义,f(x)称为I上的凸函数,当且仅当:∀x1,x2∈I,∀λ∈(0,1),有
f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2)
(3)
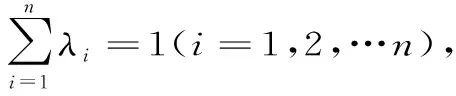
(4)
定义5 :设函数f(x)在区间I上有定义,f(x)称为I上的凸函数,当且仅当:
∀pi≥(i=1,2,…n)不全为零,∀x1,x2,…xn∈I,有
(5)
定义6 :设函数f(x)在区间I上有定义,f(x)称为I上的凸函数,当且仅当:∀x1,x2,…xn∈I,且x1 (6) 定义7 :设函数f(x)在区间I上有定义,f(x)称为I上的凸函数,当且仅当:∀x1,x2,…xn∈I,且x1 (7) 上述定义中的“≤”若改为“<”,则得f(x)为I上的严格凸函数。 区间I上可导或二阶可导的凸函数还可借助导数f′(x)的单调递增或f″(x)来判定或定义(见文献[1][2][3]),这一点本文不再赘述。 首先给出几个定理: 定理1 :定义1与定义2等价。 证明 :“定义2⟹定义1”显然成立,在(2)式中令n=2即得(1)式。 只要证明:“定义1⟹定义2”。采用反向归纳法。 1)由(1)式知:当n=2时(2)式成立。 现证n=4时(2)式成立。 事实上,∀x1,x2,x3,x4,∈I,由(1)式有 此即(2)式当n=4时成立。 一般地,对任一正整数k,重复上面方法,应用(1)式k次,可知 这表明(2)式对一切n=2k皆成立。 此即(2)式对n=k也成立。 证毕。 下面给出关于凸函数的一个论断,以引理1命名: 引理1:若函数f(x)为区间I上的凸函数,则f(x)在I内部任意一点都连续。 定理2 :定义3与定义1,2等价。 对于有理数λn∈(0,1),利用上面证明有 f(λnx1+(1-λn)x2)≤λnf(x1)+(1-λn)f(x2) 此式中令n→∞取极限并联系上式,有 f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2) 此即(3)式对任意无理数λ∈(0,1)也成立。 故定义1,2也蕴含定义3,证毕。 定理3 :定义3与定义4,5等价。 证明 “定义4⟹定义3”只要在(4)式中令n=2即得。“定义3⟹定义4”采用数学归纳法可证(定义4即为“Jensen不等式”,证明见文献[6])。“定义4⟺定义5”明显,故定理3得证。 定理4:定义3与定义6,7等价。 f(λx3+(1-λ)x1)≤λf(x3)+(1-λ)f(x1) 即 此式化简变得(6)式,故“定义3⟹定义6”成立。 反之∀λ∈(0,1),∀x1,x2∈I,,不妨设x1 由上述定理可知上文所给的凸函数几个基本定义是等价的, 区别仅是呈现的形式或各自的几何意义有所不同,但均是对凸函数本质的概述。 定义或概念是对事物本质属性的精确概括。 具体教学中,强调学生对概念的理解,目的就在于希望学生能够抓住事物的本质属性。 定义3更能体现凸函数的本质属性,其几何意义对凸函数描述很直观,现代数学中多采用这种定义。 值得一提的是,区间I上的凸函数的“凸”性仅由区间I内部函数的属性来体现,而与函数在区间端点的取值无关。 文中引理表明,在区间I内部凸函数是连续的,对应的曲线是连续曲线且呈“下凸”趋势。 同时也表明,凸函数的间断点只可能出现在区间的端点上。 [参考文献] [1] 王飞.凸函数等价性讨论[J].广西师范学院学报:自然科学版,2003,20(1):31-34. [2] 赵丹.凸函数等义的等价性证明[J].乐山师范学院学报,2008,23(12):18-21. [3] 古小敏.对凸函数定义之间等价性的进一步研究[J].重庆工商大学学报:自然科学版,2009,26(2):171-173. [4] 郭素霞.关于凸函数定义的讨论[J].衡水师专学报,2000,2(4):49-52. [5] 黄世团.几个凸函数定义的差异性及等价性[J].广西师院学报:自然科学版,1997,14(1):54-56. [6] 华东师范大学数学系. 数学分析:上册 [M].2版.北京:高等教育出版社,1991:197-203.2 定义之间等价性的证明与探讨



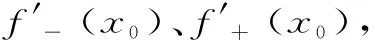
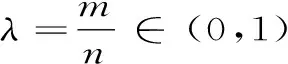


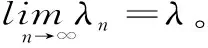

3 结束语

