陶瓷原料分类的距离判别分析法

胡祎 周景玮 胡真

（景德镇陶瓷学院信息工程学院，江西景德镇333403）

陶瓷原料分类的距离判别分析法

胡祎 周景玮 胡真

（景德镇陶瓷学院信息工程学院，江西景德镇333403）

将距离判别分析法应用于陶瓷原料分类中，建立陶瓷原料分类的距离判别分析模型。模型选用陶瓷原料的9种化学成分作为距离判别分析模型的判别因子。将陶瓷原料分为4个类别并作为距离判别分析的4个正态总体，以陶瓷原料样本实测数据作为训练样本，建立相应线性判别函数对待判样本进行分类。研究结果表明，距离判别分析模型分类性能良好，回判估计的误判率为0，可以在生产实际中推广应用。

陶瓷原料，分类，距离判别分析

1 引言

在充满激烈竞争的陶瓷产品市场中，陶瓷产品的质量是我们占据领先地位的关键性因素，而陶瓷原料质量的好歹优劣又在决定陶瓷产品的质量中起到重要作用。但由于成因不同，地质条件不同，陶瓷原料的组成和性能往往有较大的波动，从而影响陶瓷生产。因此选择合适的原料是生产优质陶瓷产品的基础。

然而陶瓷原料种类繁多，结构复杂且成分多变，现阶段又缺乏稳定的标准化原料供应，这给配方中选择原料和替代原料带来困难，所以对陶瓷原料进行科学分类和准确识别就显得非常重要了。而对原料的分类识别是一种多指标多层次的综合评价过程，需要恰当的分类识别模型和方法。蒋胜晖等[1]学者用Bayes判别分析法对陶瓷原料种类进行分类识别，取得了较好的实际应用效果。

本文以距离判别分析法建立陶瓷原料分类模型，探讨陶瓷原料的分类识别方法。模型通过选用陶瓷原料的关键性指标和训练样本，对待判样本进行了分类识别，结果表明准确率高，适宜推广应用。

2 距离判别分析法[2]

判别分析法通常是从训练样本中提取已有的各总体信息，构造一定的判别准则，以此来判断待判样本属于哪个总体。它的基本思想是比较样本和每个总体的马氏距离，并将其判定为属于马氏距离最近的那个总体。

2.1 马氏距离的概念

G={X1，X2，···，Xm}T为m元总体（m个指标），样本X={x1，x2，···，xm}T。

令μi=E(Xi)(i=1，2，···，m)，则总体均值向量为μ={μ1，μ2，···，μm}T。

总体G的协方差矩阵为:

∑=cov(G)=E[(G-μ)(G-μ)T]。

样本X与总体G的马氏距离定义为: d2(X,G)=(X-μ)T∑-1(X-μ)

2.2 两个总体的距离判别

设有2个总体G1和G2，已知来自总体Gi（i=1，2）的训练样本为···，ni）,ni为取自Gi的样本个数。则总体Gi的均值向量μi估计量为:

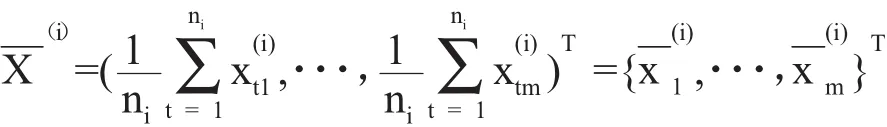
总体Gi的协方差矩阵∑i的估计为组内协方差矩阵Si∶Si= 1 ni-1Ai

当∑1=∑2=∑时，反映分散性的协方差矩阵∑的无偏估计为:

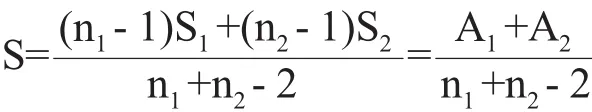
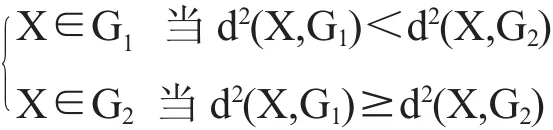
假设∑1=∑2，此时对给定的待判样本X={x1,x2, ···，xm}T判断属于哪个总体，很直观的想法是分别计算样本X到2个总体的马氏距离d2(X,G1)和d2(X, G2)，并按距离最近准则判别归类，判别规则为：利用马氏距离的概念和2个总体协方差矩阵相等的假设，可以简化马氏距离的计算公式为：d2(X,Gi) =XTS-1X-2Yi(X)(i=1,2)，式中的Yi(X)为样本X的线性函数。这样，对给定的待判样本X，计算其到各总体的马氏距离，只需计算Yi(X)即可。并且有：

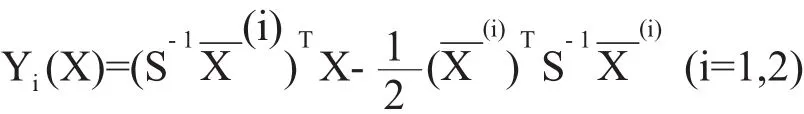
那么2个总体的距离判别准则就可以改为：

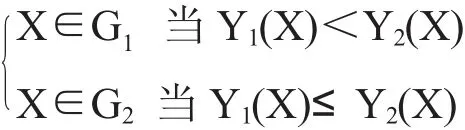
2.3 多个总体的距离判别

设有k个m元总体：G1，G2，···，Gk(k＞2)，其各自的均值向量和协方差矩阵分别为μi，∑i(i=1，2，···，k)。对任意给定的m元样本X=（x1，x2，···，xm）T判断其属于哪个总体，可以按马氏距离最近准则对X进行判别分类。首先计算样本X和k个总体的马氏距离，然后进行比较，把样本X判给距离最小的那个总体。设i=l时，若则样本X∈Gl。

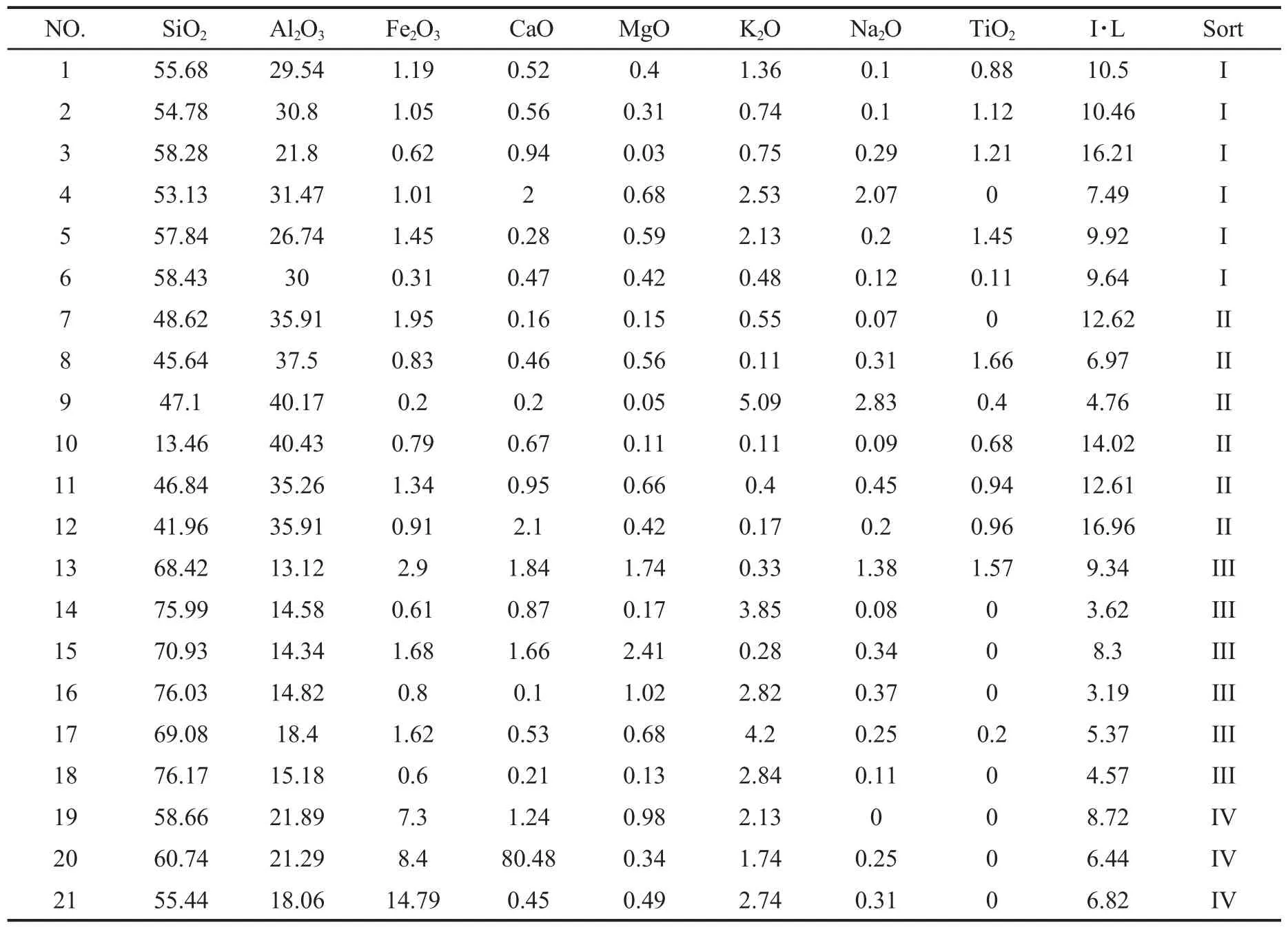
表1陶瓷原料训练样本(%)Tab.1 Samples of ceramic raw materials(%)

2.4 判别准则的评价

为评价上述判别准则的优良性，本文采用貌似误判率方法[1]来衡量。貌似误判率即为回判中判错样品的比例。具体方法如下：

设x1(k)，x2(k)，···，xn(k)(k=1，2，···，g)为来自G1，G2···，Gg的容量分别为n1，n2，···，ng的训练样本，以全体训练样本作为n1+n2+···+ng个新样品，逐个代入已建立的判别准则中判别其归属，以下式计算貌似误判率：

式中：ni(i)为属于Gi的样品被错判的个数（i=1，2，···，g）。

3 陶瓷原料分类识别的距离判别分析模型

3.1 判别参数的确定

陶瓷原料的化学成分是最直接、容易精确测量和控制的常用的特征参数。参考有关研究结果，经综合分析后，本文确定采用9种化学成分，如：SiO2，Al2O3，Fe2O3，CaO，MgO，K2O，Na2O，TiO，烧失I·L作为距离判别分析模型的判别因子。将陶瓷原料分为4类：I类，II类，III类，IV类，并作为距离判别分析的4个总体，分别对应G1，G2，G3，G4，从而建立陶瓷原料分类判别的距离判别分析函数。

3.2 距离判别分析函数

以文献[3]提供的陶瓷原料样本作为训练样本，建立距离判别分析函数。数据见表1。

假定4个总体的协方差矩阵相等，按照第二节的方法建立的距离判别函数为：

3.3 判别模型的检验

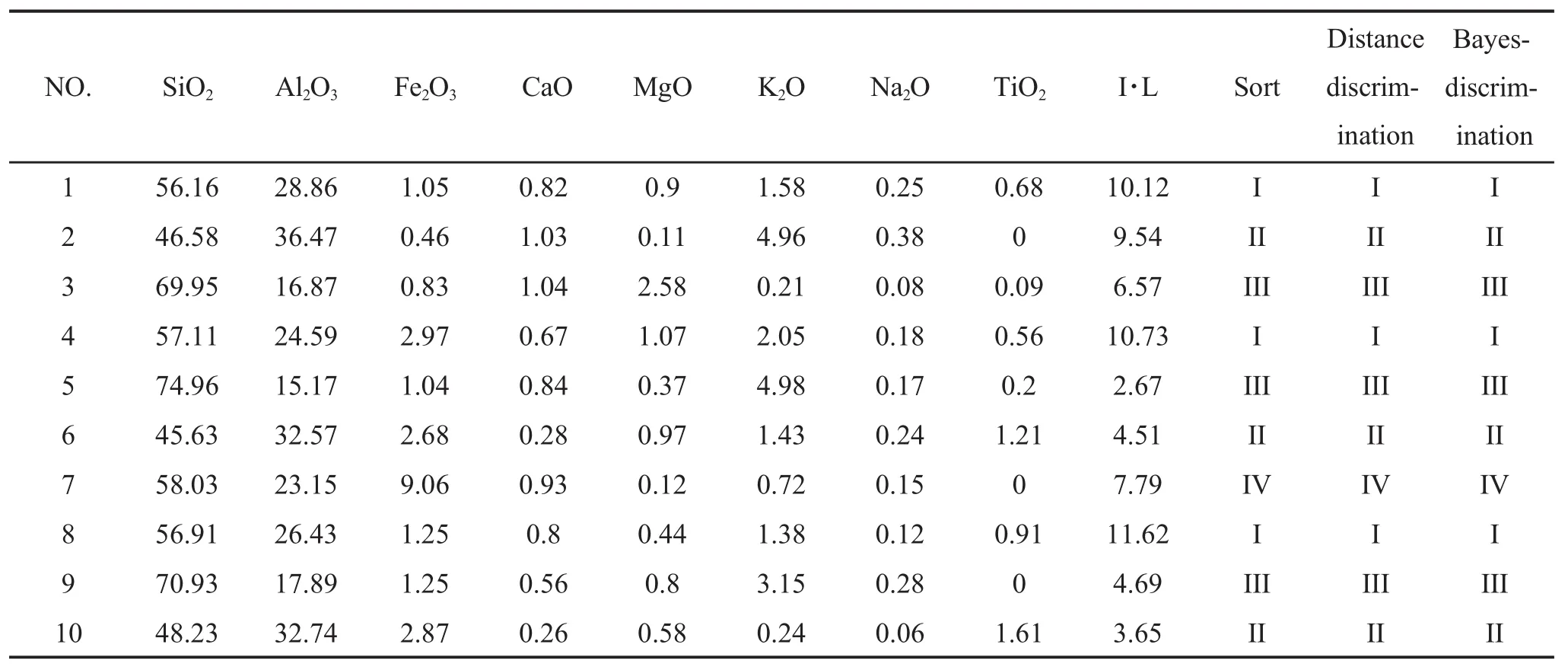
表2待判陶瓷原料样本判别结果Tab.2 Classification results of ceramic raw material samples

以2.4节中的判别评价准则对上述函数的准确性进行检验，计算得到貌似误判率为0，即以所建立的准则对训练样本进行回判，结果显示优良。

3.4 判别模型的应用和比较

应用表1的数据，得到了3.2中的距离判别分析函数，将表1中的新的样本实测数据代入距离判别函数，计算出Yi(x)(i=1，2，3，4)，并按2.2中的判别准则进行判别，得出新样本所归属的总体，判别结果见表2。同时，为了便于比较，表2中同时给出了Bayes判别方法所得的分类结果[1]。

从表2中可以看到，本文判别结果与事实相符，而且与Bayes判别分析方法所得结果完全相同。由此可见，本文的距离判别分析方法确实是一种陶瓷原料分类识别的有效方法，值得推广使用。

4 结论

陶瓷原料种类繁多，结构复杂且成分多变，但陶瓷原料的化学成分却是最直接，易测量和控制的，因此将之作为距离判别因子具有广泛的适应性和科学性。同时从模式识别的结果看，上述分类较科学：第一类粘土的SiO2含量在50%～60%左右,比第二类粘土SiO2含量高,存在游离的石英，而Al2O3的含量一般小于30%。该类粘土的示性矿物以富硅高岭石或伊利石为主,典型的代表有左云土和黑粘土；第二类粘土Al2O3含量在32%～40%之间，比第一类的Al2O3含量要高，该类粘土主要示性矿物为高岭土,结构水、有机质等，灼失量较大，它们大多数是由片状和杆状两种结构的高岭石混合组成.其典型代表是上店土，上店土主要是结晶较差的高岭石类矿物，并含有一定的高铝矿物；第三类粘土SiO2含量高，主要矿物为蒙脱石(也称微晶高岭石)。蒙脱石易于膨润和压缩，层间结合力极弱，易离解，可塑性好，干燥强度高。这类粘土大多数为风化良好的瓷土和膨润土，典型的代表有黑山膨润土和四班瓷土；第四类粘土中最突出的特点是Fe2O3含量较高，该类粘土属于软质粘土，其组织疏松，质点分散度大，典型的代表是宜兴红泥。宜兴红泥容易粉碎，因Fe2O3含量较高而显红色。而本文就是以陶瓷原料的化学成分作为判别因子，将陶瓷原料分为4类：I类，II类，III类，IV类，并作为距离判别分析的4个总体，分别对应，从而建立陶瓷原料分类判别的距离判别分析函数，利用距离判别分析法探讨了陶瓷原料的分类识别问题，并在实际中加以应用，取得了满意的判别结果，误判率为0。因此该模型为陶瓷原料配方和陶瓷生产中选择陶瓷原料提供了科学的依据和数量化、定性化的方法与途径。

1蒋胜晖,文畅平.陶瓷原料分类的Bayes判别分析法.硅酸盐通报，2008，27（2）：419～423

2宫凤强,李夕兵.距离判别分析法在岩体质量等级分类中的应用.岩石力学与工程学报，2007,26(1)：190～193

3刘付胜聪,李玉平.利用人工网络判别陶瓷原料种类.湖南大学学报（自然科学版）,2002，29(3)：40～44

4刘付胜聪,李玉平.数理统计法在陶瓷原料分类中的应用,陶瓷,2001，（1）：45～48

Abstract

Based on the principle of Mahalanobis distance discrimination analysis,a classification model of ceramic raw materials is established.Nine chemical compositions are selected as the factors for the classification model based on distance discrimination analysis.Ceramic raw materials are divided into four grades,which are considered as four normal populations in distance discrimination analysis.Linear discrimination functions are obtained through the tests of a series of ceramic raw material samples.Then a series of new samples are classified by using the model.The results show that the classification model based on distance discrimination analysis has excellent performance and the ratio of wrong-distinguishing is zero. The proposed model could be used widely in practice.

Keywords ceramic raw materials,classification,distance discrimination analysis

CLASSIFICATION OF CERAMIC RAW MATERIALS BY DISTANCE DISCRIMINATION ANALYSIS

Hu YiZhou JingweiHu Zhen
(School of Information Engineering,Jingdezhen Ceramic Institute,Jingdezhen Jiangxi 333403,China）

1000-2278（2010）04-0632-05

TQ174.4

A

2010-07-15

景德镇市科技局软科学项目(编号：2009)

胡祎，E-mail:hhhaaa123@163.com