琉球群岛海域海浪数值计算地形处理效应及试验分析
毛科峰, 陈 希, 李 妍, 萧中乐
(1. 解放军理工大学气象学院, 江苏 南京 211101; 2. 解放军96631部队, 北京 102208)
琉球群岛海域海浪数值计算地形处理效应及试验分析
毛科峰1, 陈 希1, 李 妍1, 萧中乐2
(1. 解放军理工大学气象学院, 江苏 南京 211101; 2. 解放军96631部队, 北京 102208)
针对琉球群岛海域内多岛屿复杂地形对海浪数值计算的特殊影响, 发展一种综合利用水深数据和高分辨率海岸线数据优化计算网格且引入次网格地形效应的方法, 并利用 WAVEWATCH-Ⅲ模式进行连续1个月的数值模拟试验。结果表明: 采用该方法后, 在计算网格分辨率上, 充分考虑了海岸和多岛屿地形对海浪传播的作用和多岛屿的次网格效应, 数值计算结果有明显改善。
海浪; 琉球群岛; 次网格; 数值模拟
琉球群岛海域, 是大连、青岛、厦门、釜山、仁川等港口东出太平洋的必经之路, 也是太平洋东岸及大洋洲各国出入东海和黄海的重要水运航道, 在国民经济和军事方面具有重要战略意义; 从东南陆架浅海经冲绳海槽过渡到东部西北太平洋, 日本九州至琉球、台湾一线长约600 n mile的水域内, 有众多的海峡、水道与太平洋沟通, 这里岛屿多、岛礁多、海况各异、地形复杂。深浅不一的海区和水道里, 影响海浪的因素很多, 除了风这一产生海浪的主要动力机制外, 波高的大小还取决于上风向水域的长度和宽度、海底的地形、水位的深浅等诸多因素的影响。因此该海域的海浪数值计算有一定的特殊性,同时对海浪预报、海洋工程等方面有重要的现实意义。
目前基于组成波谱能量平衡方程(如式(1))的海浪计算模型发展到了以WAM[1], SWAN[2],
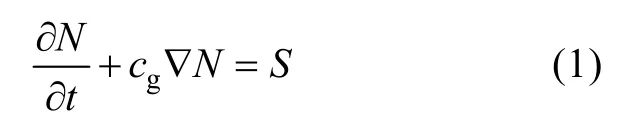
WAVEWATCH-Ⅲ[3]为代表的第三代海浪数值模式。在这个能量平衡方程中N即是波作用密度谱, 它是频率f、传播方向θ、时间t和地理空间位置的函数,cg为群速, S是能量源汇, 包括风摄入波动能量、波浪破碎和白帽破碎时能量的耗散、波与波之间的非线性相互作用引起的涡动黏滞、当水深较浅时底摩擦作用等能量的交换过程。基于(1)式进行数值计算时, 对谱空间(f,θ)或者(k,θ)和地理空间的计算分辨率选择是十分重要的问题, 它对海浪计算的精度和效率有较大影响[4]。为了在琉球群岛海域内更准确地计算海浪, 必须提高海浪模式的空间网格分辨率来反映岛屿地形分布、海底地形及水深变化, 但是分辨率的提高又受到水深地形资料、风场资料的分辨率以及计算效率的限制。Tolman和Chawla[4]曾指出某一空间分辨率计算网格未体现出的岛屿群和障碍物是海浪计算和预报误差的主要来源之一。为了解决这一问题, Holthuijsen[2]提出了在SWAN模式中考虑次网格障碍物对海浪能量传播的抑制作用的思想,Tolman[5]将这种方法用在 WAVEWATCH-Ⅲ模式中,考虑岛屿群和局部海冰的次网格效应对海浪传播的影响。但是如何科学方便地在海浪数值计算中处理多岛屿的分布和复杂海岸线等特征, 如何准确地设计次网格的计算方案还值得深入研究。鉴于此, 本文发展一种在群岛海域内综合利用水深数据和高分辨率海岸线数据优化海浪数值计算网格且引入岛屿次网格地形效应的方法, 利用该方法和WAVEWATCH-Ⅲ模式进行了数值试验并利用实测资料分析了数值试验结果。
1 海浪数值模式和数值计算方案
琉球群岛海域内的琉球海脊将东海大陆架东侧的深海区分割出来, 在东海大陆架和琉球海脊之间,形成狭长的深海区域——冲绳海槽。琉球海脊在600 m以浅主要以西表—石垣—宫古、冲绳岛、奄美大岛的岛链形式存在。在600 m以深, 几个岛链相连,除了冲绳岛以南的庆良间水道以外, 形成了完整的东北—西南向的海脊, 如图1所示, 图中等值线为水深值分布, 单位为 m。根据琉球海域的特点, 利用WAVEWATCH-Ⅲ模式进行海浪模拟是合适的。WAVEWATCH-Ⅲ模式合理地考虑了风浪相互作用、非线性相互作用、耗散及底摩擦等作用, 能比较准确地模拟复杂的潮流、地形、风场环境下的波浪场, 该模式是以上文的(1)式组成波谱能量平衡方程为基础,球坐标系下该方程可表式为:
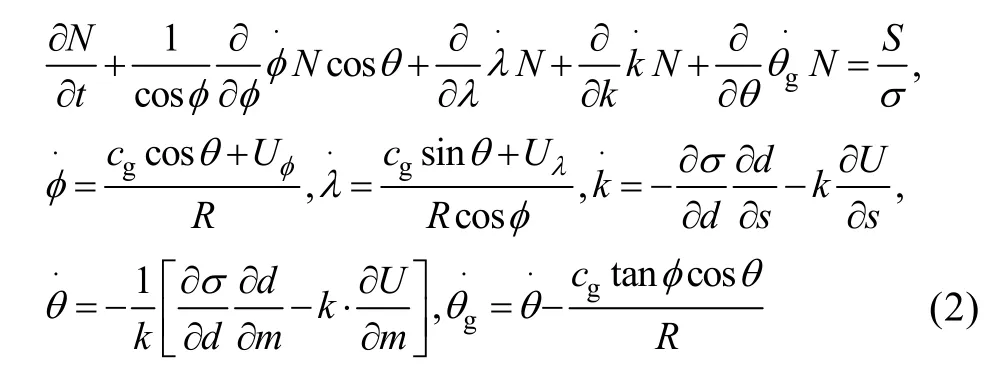
式(2)中k为波数, θ为波向, U为平均流速(对水深、时间平均),为群速, σ为相对频率,区别于绝对频率是经度, 是纬度, R为地球半径, d为水深,是沿纬向、经向的流速, S是源汇项。源汇项S包含风摄入波动能量项Sin、非线性的波-波相互作用项Snl, 耗散项(白浪效应)Sds和底摩擦项Sbot; 即通常情况下, 源汇项S可表示为:
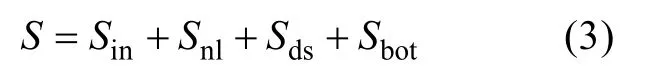
对(2)式进行数值求解时采用分裂算法, 首先考虑水深在时间上的变化以及对应波数网格上的变化; 这样不考虑(暂时的)水面变化的影响后, 波数网格就是不变的, 水深也是准稳定的; 然后分步计算(2)式左边的海浪谱在物理空间上的传播、波数空间上的传播项和(2)式右边的源函数项。在球坐标下, 将海浪在地理空间传播表示为:
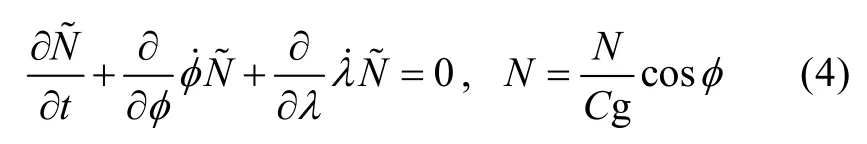
本文在 WAVEWATCH-Ⅲ中采用 ULTIMATE QUICKEST数值格式[6], 这个格式把纬向传播和径向传播分开进行计算, 计算顺序是任意, 在 方向上,第i和i-1这两个格点之间的通量为Fi,−。

式中j, l和m分别是纬度λ, 谱空间θ和k方向上的离散网格计数, n表示时间层, Cu是作用量密度的曲率, C是带有符号的CFL数,bφ˙代表两个格点之间格点单元边界上的传播速度,iφ˙代表格点上的传播速度, Nb代表格点单元边界上的作用量, Ni代表第 i个格点上的作用量。在时, 该格式可得到稳定解。故而该格式在 方向上也可表示为:
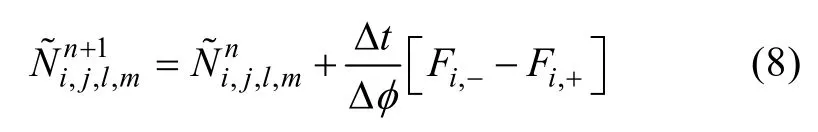
更改下标和相应的增量, 同样可得 方向上的传播格式。
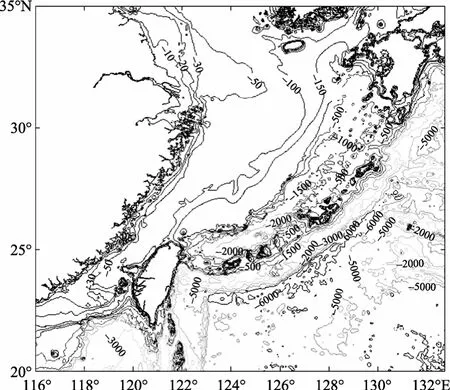
图1 东中国海及琉球群岛海域地形Fig. 1 Bathymetry distribution in the China offshore area and Ryukyu area
2 群岛海域内复杂地形的处理方案
2.1 优化海浪数值计算网格的方法
WAVEWATCH-Ⅲ的数值计算网格利用“干湿”属性来区分网格点是陆地或是海洋, 海洋上的“湿”网格是有效计算网格, 陆地“干”网格是计算的边界。如果计算网格中, 有部分网格的“干湿”属性是虚假的, 那么海浪数值模拟时必然会造成误差。本文在设计琉球群岛海域海浪计算网格时, 利用海图中存储的一些海岸线、岛屿、数据, 对网格点进行海陆属性判别, 优化计算网格, 具体方法是:第一步, 将大陆或者岛屿当作闭合的任意多边形, 得到闭合多边形数据; 第二步, 通过判断计算网格点与这些多边形的位置关系, 来区分每个网格点的海陆属性, 在多边形内部的格点判别为陆地, 多边形外的格点判别为海洋。本文引入了一种高效的判断点与多边形位置关系的算法[7]即夹角和法: 将整个大陆和任意岛屿看成一个边数为 n的多边形,其顶点序列为,海浪数值计算网格作为待判别的点为连接 P和多边形的各个顶点, 计算其夹角和, 其中顺时针向为正, 逆时针方向为负, 如图2所示。

图2 点与多边形的关系Fig. 2 Ubiety between points and polygons
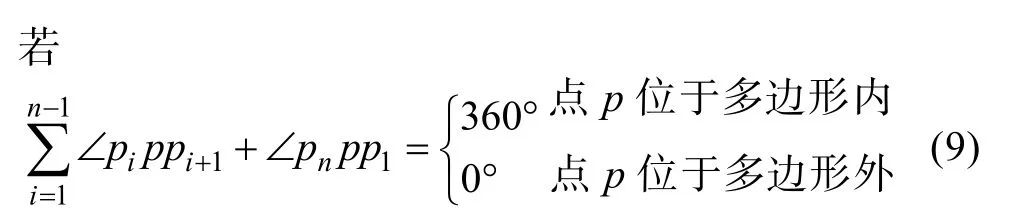
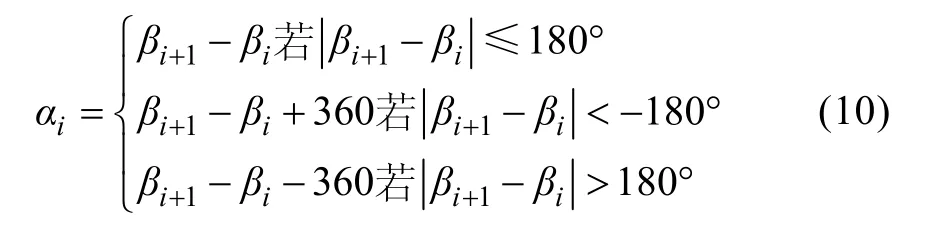
经过这两个步骤优化后的计算网格融合了岛屿和海岸线信息, 判别了计算格点的“干湿”属性即陆地和海洋属性, 如图2所示, 在岛屿闭合多边形内的计算点被判别为“干”属性点, 之外的为“湿”属性点。然后在海上的“湿”网格上进行水深插值, 获得计算网格点上的水深值。
2.2 次网格地形效应的计算方案
经过优化的海浪数值计算网格, 能够在计算网格分辨率的水平上充分表现多岛屿的分布和海岸的地形。如果仅采用这种方法, 随着计算网格分辨率的提高, 能够描述的岛屿地形分布就越细致, 但是计算网格的分辨率不可能无限提高。在一定计算分辨率水平下, 仍然有比计算网格尺度更小的岛屿等地形特征不能被描述, 如图3所示有若干个类似图中A点所指的小岛屿, 在这种计算分辨率水平下, 它周围的计算格点都是“湿”属性, 在计算时, 便把它“忽略”了。因此, 有必要在海浪数值计算中引入次网格地形效应, 充分考虑计算网格分辨所不能分辨的小岛屿的地形作用。
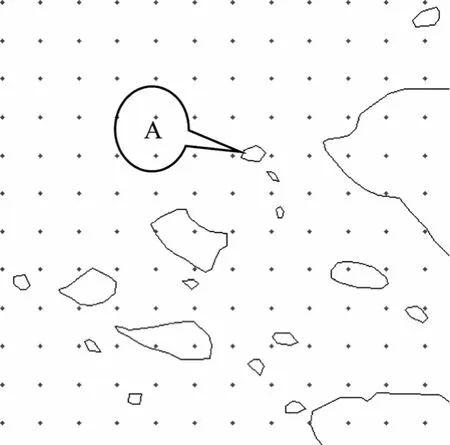
图3 计算网格和岛屿地形分布Fig. 3 Island distribution and computing grid
在(8)式中若在第i个计算格点所在的单元格内,有一个未被网格分辨的小岛屿或障碍物, 如图 4, 为了在这个计算单元格内考虑它对海浪传播的阻碍作用, 在计算单元边界的两个方向上定义能通量穿透度系数系数的值域为: 0~1, 取0时表示次网格岛屿的影响作用为封闭边界, 在这个计算单元的海浪能通量被完全阻碍, 取 1时表示没有次网格岛屿。于是(8)式可以写为:
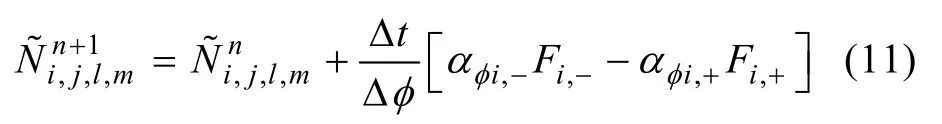
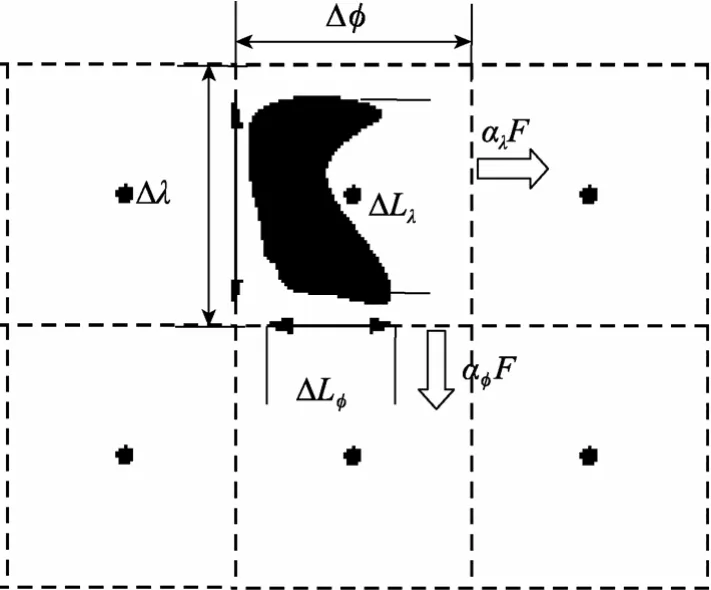
图4 计算网格和次网格尺度的岛屿Fig. 4 Computation grid and sub-grid island
通过次网格能通量穿透度系数的引入来抑制计算格点单元之间的能量通量, 体现了次网格尺度岛屿对海浪的阻碍作用。在优化过的计算网格上, 利用上述判断点与多边形位置关系的夹角和法, 判别计算网格的“湿”属性海洋计算点和未被计算网格分辨的小岛屿的位置关系, 搜索出需要计算能通量穿透度系数的计算格点单元, 然后求计算格点单元的穿透度系数如图 4, 在 方向上在∆L为 方向岛屿的宽度,∆ 为 方向格点单元的宽度, ∆Lφ为 方向岛屿的宽度, ∆ 为 方向格点单元的宽度。
3 数值试验与分析
3.1 试验方案
对琉球群岛海域 2004年 10月的海浪过程进行模拟, 并与实测资料对比分析: 计算范围为 20°~35°N, 116°~132.75°E, 格距为 15′; 模式包括风浪相互作用、波波相互作用、白帽耗散、底摩擦作用等物理过程。模拟时段从2004年10月1日02时以120 s的时间步长积分到的10月31日23时。由于该时段内有 3次台风过程影响该海域, 故试验所用的风场根据Holland[8]台风风场模型和QuickSCAT/NCEP混合风场[9]合成。试验1采用本文提出的综合利用水深数据和高分辨率海岸线数据优化计算网格且引入次网格地形效应的方法进行模拟, 试验 2直接用ETOPO2水深资料并且不考虑次网格地形效应进行模拟。图5中给出了琉球群岛海域附近的岛屿分布,圆点表示计算网格的陆地点, “×”点表示次网格点,正方形标出的位置为海浪测站的3个站点: NAHA站、NAKA站和NASE站。

图5 琉球群岛海域陆地点和次网格点Fig. 5 Land points and sub-grid points in the Ryukyu offshore area
3.2 结果分析
这 3个测站的海浪有效波高每两小时有一个观测值, 分别将试验1和试验2三个测站2004年10月的有效波高模拟结果的误差进行统计, 结果如表 1所示, 试验1中有效波高的偏度、均方根误差、平均绝对误差、均方相对误差、平均相对误差均明显小于试验2, 其中试验1较试验2的偏度降低了0.31 m,平均相对误差降低约 12%。这说明在综合利用水深数据和高分辨率海岸线数据优化计算网格和在海浪数值计算中引入次网格地形效应后海浪有效波高的模拟的精度有了较大提高了。这在图6中 3个测站10月的有效波高模拟值与实测值的散点图也能得到证明。图7是两个试验方案的模拟结果和3个浮标资料的时间序列比较图, 图 7表明在 NAHA站和NASE站具有同样的特点: 试验2的有效波高值较浮标观测值明显偏大, 试验1的较试验2的值偏小且更接近浮标观测值, 可见在这两个浮标站, 试验1结果明显优于试验2; 在NAKA站, 试验1和2模拟的有效波高值几乎完全一致, 两个试验方案模拟结果没有差别, 而且与浮标观测值十分接近, 有效波高模拟误差很小。究其原因: 如图6试验2所示, NAHA站和 NASE站附近均有若干个小岛屿, 并未被计算
网格分辨为陆地点, 故而在试验 2中这是导致NAHA站和NASE站有效波高模拟误差的主要原因之一。在试验1中引入了岛屿次网格地形效应, 考虑了这些岛屿存在对海浪的影响, 克服了有效波高模拟偏大的误差, 这说明本文的次网格作用计算方案能够体现出比计算网格尺度小的岛屿对海浪传播明显的抑制作用。两种试验方案结果的差别在NAKA站却不存在, 是因为该站附近没有其他的小岛屿, 因而该点附近也没有次网格效应的影响。如图 8是两种试验方案在计算区域内10月份有效波高的月平均值之差的分布图, 试验1与试验2相比, 具有明显的负系统偏差, 月平均有效波高之差的最大值达0.7 m,同时与图 5对比可以发现月平均有效波高有明显差异的地方就集中在考虑次网格效应的计算网格点附近。因此可以说, 岛屿次网格效应对有效波高的模拟误差有明显的影响, 但是这种影响也是有局地性的,这可能是岛屿次网格效应对涌浪传播的阻碍和抑制作用导致的。

表1 两次试验的误差Tab. 1 Errors between observed data and computation results for two experiments
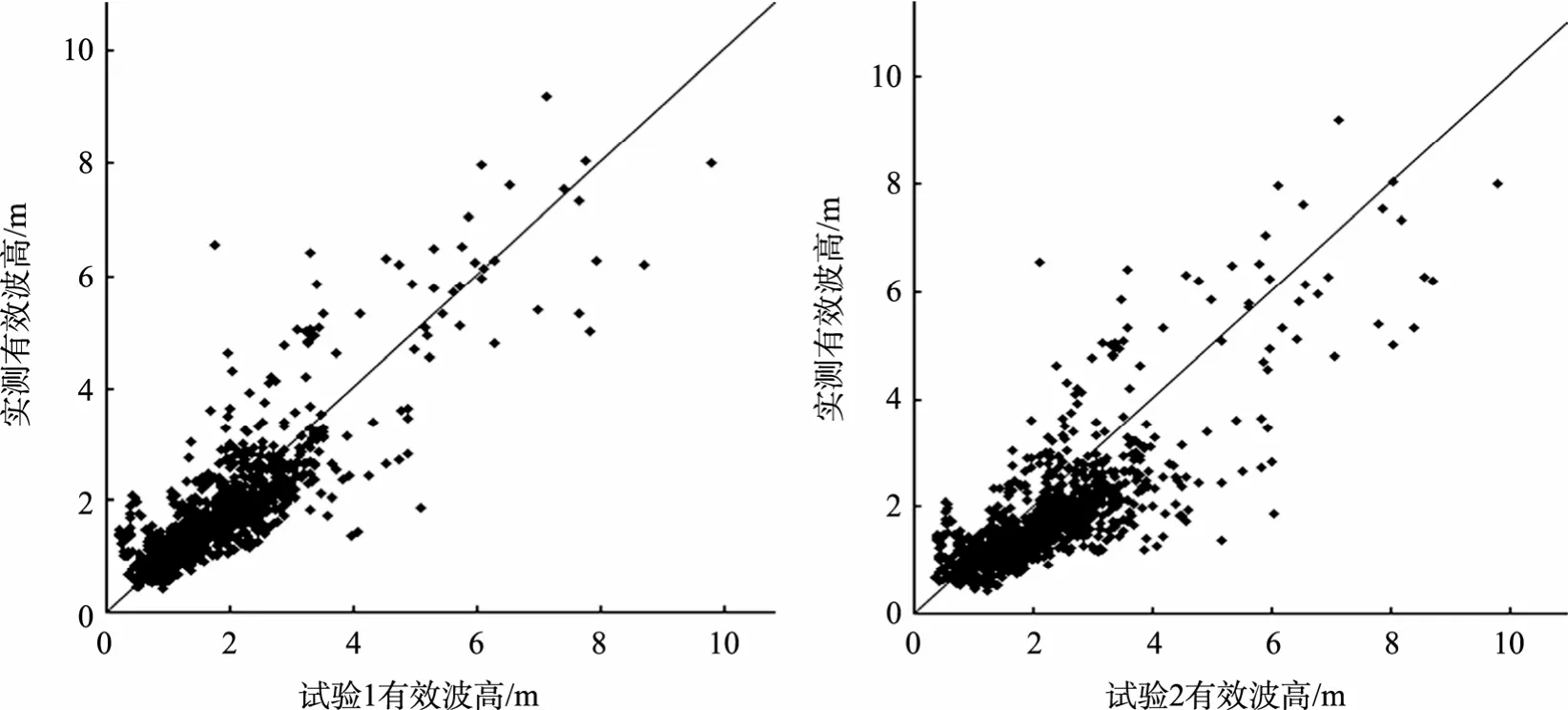
图6 3个测站波高模拟值与实测值的散点图Fig. 6 Scatter plots of wave heights of observed data at three sites and computation results computed for two experiments
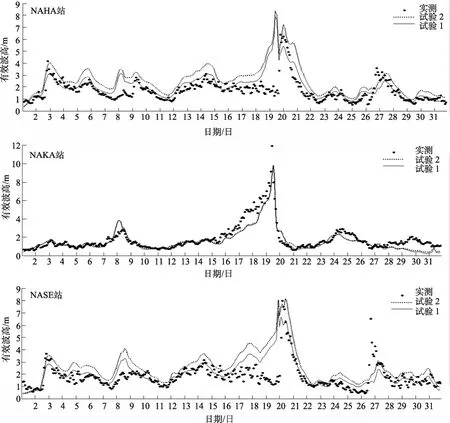
图7 3个测站10月份的有效波高模拟值与实测值的比较Fig. 7 Comparison of wave heights between model results and observations in October at three sites
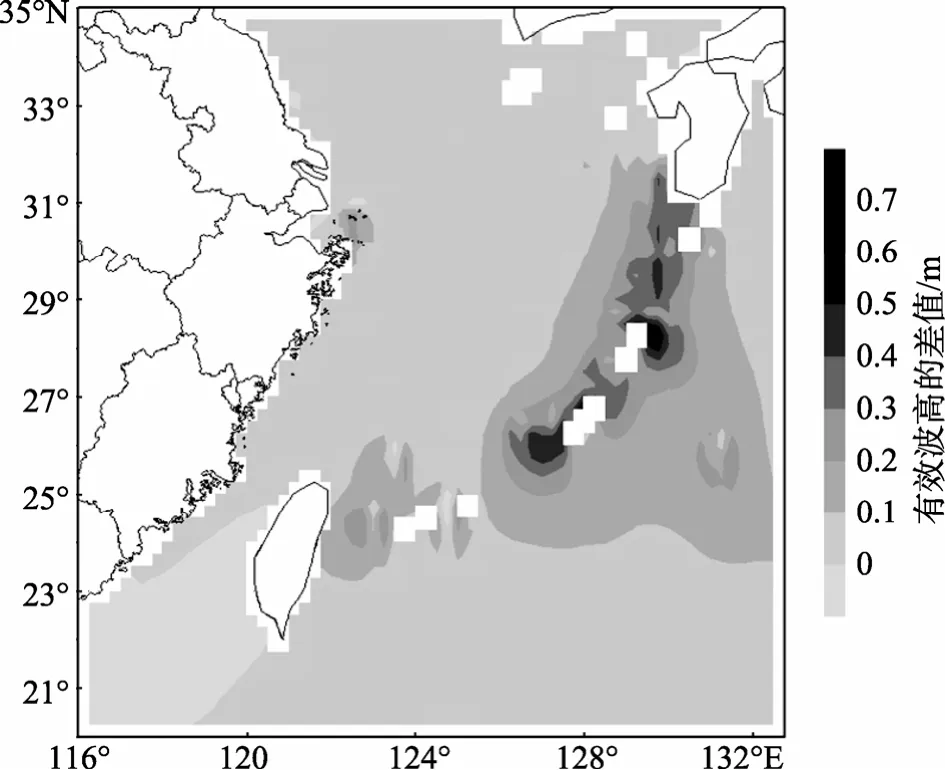
图8 两种模拟方案10月份平均有效波高的差值分布Fig. 8 Mean difference maps of the wave heights for the month of October between two simulation schemes
4 结论
1)综合利用水深数据和高分辨率海岸线数据来判别海浪数值计算网格点的海陆类型, 使计算网格设计更加优化合理, 该方法能够在计算网格的分辨率上充分体现多岛屿的分布特征。
2)在琉球群岛海域内, 对多岛屿复杂地形是海浪模拟的主要误差源; 引入岛屿次网格作用计算方案后, 能够体现出比计算网格尺度小的岛屿对海浪传播有明显的抑制作用, 可以提高海浪模拟的精度,通过与浮标实测资料的对比表明, 有效波高模拟的平均相对误差降低约12%。
3)岛屿次网格效应对有效波高的模拟误差有明显的影响, 但影响是局地性的, 这可能是岛屿次网格效应对涌浪传播的阻碍和抑制作用导致的。
4)通过琉球群岛海域海浪模拟数值试验表明本文发展的优化海浪数值计算网格且引入次网格地形效应的方法具有实用性和有效性, 这种方法, 为多岛屿复杂地形条件下海浪数值研究打下基础。
[1] WAMDI Group. The WAM model-A third generation ocean wave prediction model[J]. J Phys Oceanography, 1988, 18(8): 1 775-1 810.
[2] Holthuijsen L H. SWAN III version 40.45 USER MANUAL[R]. Delft of Netherlands: Delft University of Technology, 2006.
[3] Tolman H L. User manual and system documentation of WAVEWATCH-III version 2.22[EB/OL]. http://NOAA /NWS / NCEP / MMAB Technical Note, 2002-12-18.
[4] Tolman H L. Alleviating the garden sprinkler effect in wind wave models[J]. Ocean Modelling, 2002, 4(3):269-289.
[5] Hendrik L T. Treatment of unresolved islands and ice in wind wave models[J]. Ocean Modelling, 2003, 5(3):219-231.
[6] Leonard B P. A stable and accurate convective modeling procedure based on quadratic upstream interpolation[J]. Comput Methods Appl Mech Engng, 1979,19(1): 59-98.
[7] Feito F R, Tomes J C, Urena L A. Orientation simplicity and inclusion test for planar polygons[J].Com-puter&Graphics, 1995, 19(4): 595-600.
[8] Holland G J. An Analytic model of the wind and pressure profiles in Hurricanes[J]. Mon Wea Rev, 1980,108(8): 1 212-1 215.
[9] 李明悝, 侯一筠. 利用 QuikSCAT/NCEP混合风场及WAVEWATCH模拟东中国海风浪场[J].海洋科学,2005, 29(6): 9-12.
Received: Mar., 19, 2009
Key words:ocean wave; Ryukyu area; sub-grid; numerical modeling
Abstract:In order to describe complex multi-island terrain and coastlines adequately for modeling ocean wave in sea areas by Ryukyu, an algorithm based on high-resolution bathymetry and coastline data was developed to optimize the design of wave computation grid and introduce sub-grid terrain effect into wave computation.WAVEWATCH-Ⅲ was used to carry on continuous numerical simulation for a month. It was validated that the impact of complex coastline and multi-island on the wave propagation, computation grid resolution, and sub-grid effect of the multi-island effect was adequately address. Application of this algorithm led to much improved computational results.
(本文编辑: 刘珊珊)
Numerical simulation for ocean wave in sea areas by Ryukyu
MAO Ke-feng1, CHEN Xi1, LI Yan1, XIAO Zhong-le2
(1. Institute of Meteorology. PLA University of Science and Technology, Nanjing 211101,China;2. No.96631 army of PLA,Beijing 102208,China)
P731
A
1000-3096(2010)11-0091-06
2009-03-19;
2010-07-10
军队重点基金; 卫星海洋环境动力学国家重点实验室开放研究基金(SOED1009)
毛科峰(1981-), 男, 湖南常德人, 解放军理工大学气象学院博士研究生, 研究方向: 物理海洋, 电话: 025-80831609, E-mail: maomaopla@163.com

