HPGe探测器死层厚度及点源效率函数研究

钱 楠 王德忠 白云飞 刘 诚 张 勇 杨永亮

1（上海交通大学 上海 200240）

2（秦山核电有限公司 海盐 314300）

作为一种先进的无损检测方法(NDT)，层析 γ扫描技术(Tomographic Gamma-ray Scanning，TGS)可对被测物体进行立体扫描测定其活度(垂直方向分层，每层进行平移加旋转扫描)。该物体被分割为许多体素，并设每个体素中衰减系数和放射性核素都均匀分布。再通过附加外放射源对被测物扫描，得到被探测物内部衰减系数分布。由衰减系数分布及被测物内放射性物质产生的计数进行衰减校正，可得到放射性物质活度及位置分布。其中，发射图像重建计算系基于探测器的探测效率矩阵，因此效率矩阵中各元素值准确与否，是该技术测量结果准确与否的关键因素之一[1]。

计算效率矩阵的方法主要有三种：(1) 数学推导；(2) 实验测定；(3) 蒙特卡罗(MC)模拟。由于晶体结构复杂，数学推导所涉及积分计算难度较大，不易求解。测定不同位置的探测效率以获得效率矩阵，则需大量测量，获得的效率矩阵精度也不高。MC法计算效率矩阵可避免上述弊端，也可避免实验中不确定因素引入的误差[2]。Hannele Aaltonen等[3]发现，对60－1800 keV光子，不同探测器和体源的实验效率与MC法计算的效率一致。本文使用基于MCNP程序(Monte Carlo N-Particle Code)[4]计算点源不同位置探测效率拟合出效率函数。该软件由美国Los Alamos国家实验室开发的模拟中子、光子和电子在物质中输运过程的通用蒙特卡罗程序，广泛应用于核探测器的效率计算中。

MC法计算探测器效率的精度主要依赖于探测器物理模型的精度。射线穿越晶体死层时不产生电子空穴对，相当于减少了锗晶体的有效体积，因此死层厚度的准确性对计算结果有很大影响。厂商提供的探测器死层参数不准确，以及使用过程中的死层厚度增加，使建立探测器模型时无法知道准确的死层厚度。这就给探测器效率计算带来误差，因此，进行MC法计算效率前，须对探测器的物理模型进行必要的修正。

1 探测器效率计算方法及原理

探测器的探测效率(ε)系探测器的几何效率(εj)、屏蔽效率(εp)、源自吸收(εz)和探测器本征效率(εb)的乘积[5]，即 ε=εjεpεzεb；本文所涉的源与探测器间无吸收材料(εp=1)，且为点源(故 εz=1)，则 ε=εjεb。εj的值与源-探测器距离及探测器对源所张立体角 Ω有关。εb主要与探测器尺寸、死层厚度以及入射粒子的径迹长度等因素有关。对于图 1所示几何，ε可用式(1)表示[6]：

式中，µw是探测器窗的线性吸收系数，w是γ射线在探测器窗中的径迹长度，µ是锗的线性吸收系数，d是γ射线在锗晶体死层中的径迹长度，l是γ射线在锗晶体有效区域中的径迹长度，τ是 γ射线在锗晶体中光电效应的作用截面，σ是γ射线在锗晶体中康普顿散射的作用截面，κ是γ射线经康普顿散射后能量全部沉积在晶体中的概率。

图1 探测器简图Fig.1 A sketch of the detector

其中，Ω、w、d、l均为源到探测器轴线距离及源到探测器端面垂直距离的函数。当探测器一定时，µw、µ、τ、σ和κ仅与射线能量有关，因此ε是源到探测器轴线距离、源到探测器端面垂直距离以及射线能量的函数。本文先对一定能量的射线计算不同位置的点源探测效率，拟合出点源效率函数；再在不同能量下计算效率函数，拟合出各效率函数参数与能量的关系，从而得到探测效率与射线能量、几何空间参数的关系。

2 实验及计算结果

2.1 死层厚度修正方法

为进行探测器晶体死层厚度调节，先用刻度源在选定位置测量探测效率。然后根据已有的晶体参数建立MCNP计算模型，计算与实验位置相同的点源的探测效率，将计算值与实验值进行比较，若误差超出可接受范围，则须改变晶体死层厚度，再次对模型进行计算，直到误差在允许范围内[7]。计算框图见图2。

图2 死层厚度修正流程Fig.2 Flowchart of thickness modification of dead layer

2.2 实验模型

实验使用60Co点源，用HPGe (GC1520型，Canberra公司)测量其1332 keV γ射线。为减小源位置引入的实验误差，在确保探测效率不至过低的前提下，将放射源尽量远离探测器，以减小探测器符合相加的影响。如图3所示，从离探测器距离33.5 cm处每隔4 cm布置60Co点源，测量一次，直到69.5 cm处；在前3个位置还将源置于偏离探测器轴心处，偏离距离分别为4、8、12、16 cm。建立的模型采用Canberra公司提供的参数，HPGe晶体为Φ48.5 mm×39.5 mm，冷井为Φ8 mm× 25 mm，死层厚度0.5 mm。

2.3 死层厚度修正

用该公司提供的死层厚度建立的模型，其计算结果与实验结果(表1)之间误差相当大，计算结果均大于实验结果，最大误差达19.39%。说明该HPGe在长期使用过程中死层厚度不断增加，其有效体积不断减少。在0.5–1.4 mm范围内调节死层厚度，计算所有测量位置的计算值与实验值之间的相对误差平均值(图4)。可以看出，平均误差与死层厚度有明显的线性关系，当相对误差平均值等于零时所对应的死层厚度即实际死层厚度。

表1 实验结果及模型计算结果Table 1 Experiment and calculation result

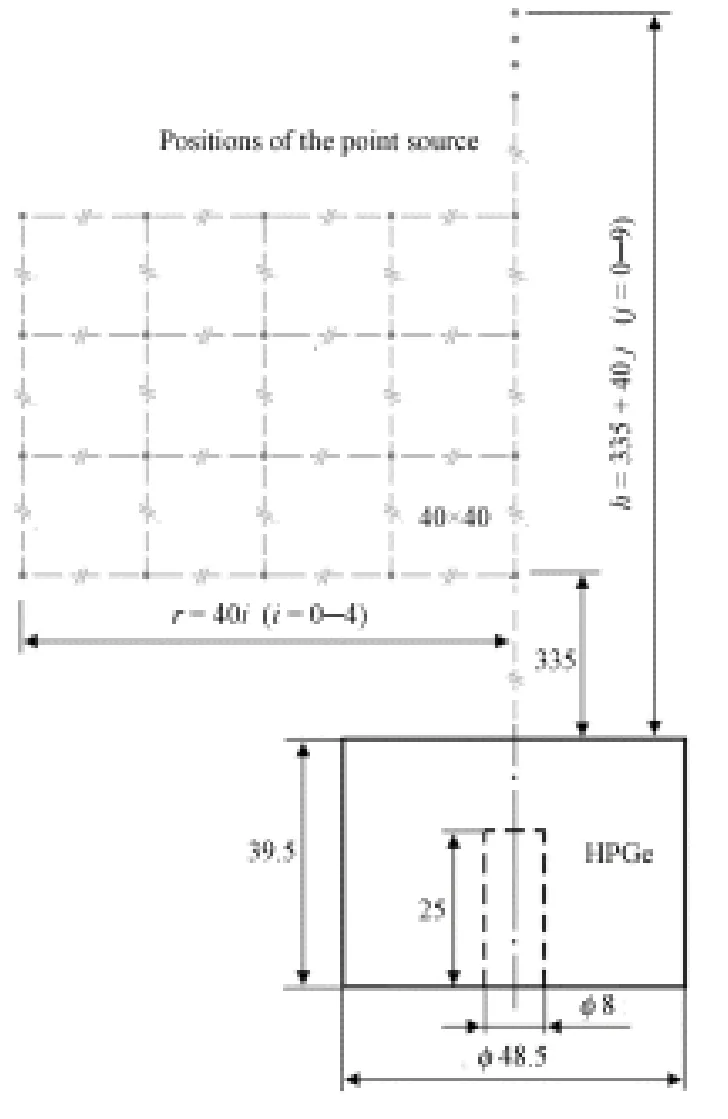
图3 实验布点Fig.3 The distribution of the experiment

经拟合，得到死层厚度与相对误差间的线性关系如下：

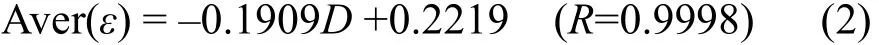
其中，Aver(ε)是平均误差，D是死层厚度。由式(2)，D=1.16 mm时，Aver(ε)=0。因此修正后的死层厚度为1.16 mm。其对应的各位置的探测效率如表1中所示。其结果明显优于修正前计算所得探测效率。

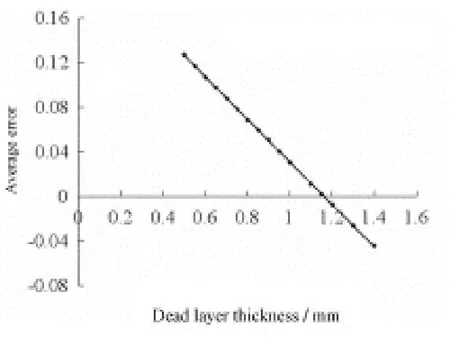
图4 死层厚度对应的误差平均值Fig.4 Average relative error of different dead layer thickness

由于探测器结构不同，则死层厚度与相对误差平均值的关系式中的参数也不同，使用此种方法修正死层厚度时只需少量的探测效率计算即可确定实际死层厚度。

2.4 计算效率函数

若已知点源的效率函数，当代入点源所在位置参数后即可求得所需位置的效率，从而求得效率矩阵。使用死层校正后计算模型所得效率与实验结果误差很小，可认为修正后模型为准确的探测器模型。在计算效率函数的过程中，考虑到效率函数必须覆盖效率矩阵中的所有点。因此，计算过程中的源-探测器距h=25.5–97.5 cm，每隔4 cm取一个计算位置。源-探测器轴线距离r =0–48 cm，每隔4 cm取一个测量位置。根据所求得探测效率曲线，通过取下列形式的点源效率函数进行拟合[4]：

式中，ε(ai,E,h,r)为探测器对点源的探测效率。ai(i=1,2,3,4,5)是待定参数，这些量与探测器自身性质及射线能量有关。绘制的三维数据及拟合曲线如图5所示。效率函数参数分别为0.001852、0.037965、1427.731、–25.9571、8.117516，相关系数 R=0.9938，SD= 2.422×10–6。

由于桶及探测器的对称性，仅需计算探测器中心线一侧的效率函数即可。半桶平面所在区域h=40–100 cm，r =0–30 cm区域内的一个半圆。由图6，所需部分拟合结果与计算值误差之间误差不大，图中数据点相对误差绝对值的平均值为 3.08%，相对误差的绝对值绝大部分在 5%以内，数据拟合效果非常理想。误差大数据点集中于远离晶体轴线区域，由于层析γ扫描技术分析的桶所覆盖区域不涉及这片误差较大数据区域，因此使用拟合公式方法所求效率矩阵是可行的。

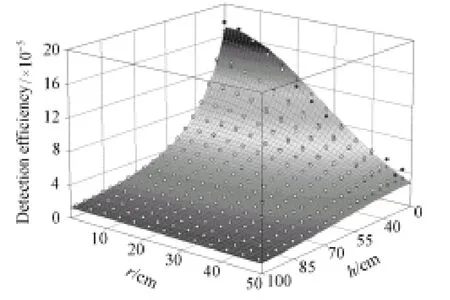
图5 HPGe探测器对空间不同位置60Co点源探测效率计算结果拟合图Fig.5 Plot of counting efficiency of the HPGe detector for a 60Co point source at different positions

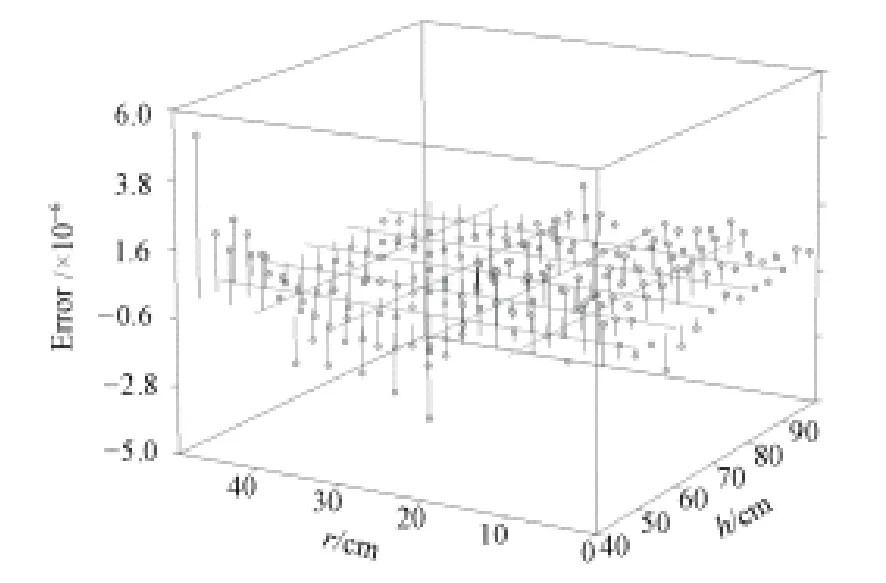
图6 部分空间位置Co-60点源探测效率计算结果拟合误差Fig.6 Fitting errors of calculated detection efficiency for 60Co point source in different positions

在经过死层厚度修正的计算模型基础上，又选取了443.98、564.03、657.75、937.48 keV四种能量射线使用 MCNP程序进行了效率计算并拟合出效率函数。效率函数参数ai(i=1,2,3,4,5)、相关系数R、标准差S.D.的拟合结果列于表2。

表2 点源效率函数参数拟合结果Table 2 Fitting parameters of the efficiency function for point sources

由图 7，拟合函数计算所得效率值与使用蒙特卡罗方法计算的效率值之间误差非常小。但射线能量为443.98、564.03、657.75、937.48、1332 keV时，两者平均相对误差分别为2.08%、2.17%、2.46%、2.37%、2.62%。相对误差绝大部分在 5%以内，使用该函数进行效率拟合非常合适，拟合效果很好。

由于式(3)只给出能量一定的情况下，探测效率与r和h之间的关系，现进一步获得能量与探测效率关系。考虑到不同能量下只有ai(i=1,2,3,4,5)与能量有关，因此寻找ai与能量关系。经拟合计算，其关系如式(4)所示：

表3 效率函数参数与能量关系拟合结果Table 3 Fitting results of the efficiency function parameters and radiation energies

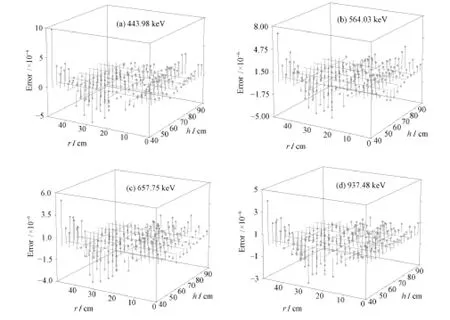
图7 部分空间位置点源探测效率计算结果拟合误差Fig.7 Fitting errors of calculated detection efficiency for point source in different positions

表 4中，εexp表示实验求得效率，ε''com表示修改后模型计算效率。其中：

由式(4)计算出能量为443.98、564.03、657.75、937.48、1332 keV时，探测效率与使用蒙特卡罗方法计算的探测效率平均相对误差分别为 2.44%、3.06%、3.67%、3.45%、3.25%。由于拟合公式是蒙特卡罗方法计算结果的进一步拟合，这种近似过程不可避免地会增大误差。尽管结果精度变差但仍在许可范围内。进一步对比试验结果及公式计算结果，两者间平均相对误差为 2.18%。说明公式计算精度仍然很高，完全能够达到效率矩阵计算要求。因此，在求效率时可先通过式(4)代入能量E，确定该能量下的效率函数参数，再代入该点源位置参量r和h，即可快速准确求得该位置的效率。

表4 实验结果及公式计算结果Table 4 Experiment and calculation result

3 讨论与结论

(1) 使用实验探测器晶体初始尺寸所建立模型进行探测效率计算时，发现效率最大误差将达到19%。当探测器晶体死层厚度修正为1.16 mm，两者间误差最小，绝大多数位置误差在 4%以内，误差绝对值的平均值为2.4%。说明死层厚度对探测效率计算有非常大的影响，计算探测效率前必须修正死层厚度；

(2) 在研究中发现，死层厚度与计算值与实验值误差的平均值之间存在线性关系，所以在修正死层厚度时可以不用计算大量不同死层厚度来寻找最合适的厚度，只需求得死层厚度与各测量点的计算与实验效率相对误差平均值之间关系。当误差的平均值为零时，对应的死层厚度就是最优死层厚度。使用这种方法计算死层厚度可节约大量计算时间；

(3) 使用修正后的探测器参数计算点源的探测效率，拟合出点源对探测器效率函数。TGS技术所需区域内数据点相对误差绝对值的平均值为3.08%，误差绝大部分在5%以内，拟合效果很好，可以使用拟合效率函数求解效率矩阵；

(4) 在经过死层厚度修正的计算模型基础上，进一步模拟多个能量的探测效率函数，得到探测效率函数参量ai(i=1,2,3,4,5)与能量E之间关系式，进一步完善了点源效率公式。

1 肖雪夫, 夏益华, 吕峰, 等. 辐射防护, 2001, 21: 1–10 XIAO Xuefu, XIA Yihua, LÜ Feng, et al. Radiation Protection, 2001, 21: 1–10

2 王崇杰, 张爱莲, 吕建洲. 核技术, 2006, 29: 77–80 WANG Chongjie, ZHANG Ailian, LÜ Jianzhou. Nucl Tech, 2006, 29: 77–80

3 Hannele Aaltonen, Seppo Klemola, Finn Ugletveit. Nucl Instr Meth Phys A, 1994, 339: 87–91

4 张富利, 曲德成, 杨国山. 核技术, 2007, 30: 231–235 ZHANG Fuli, QU Decheng, YANG Guoshan. Nucl Tech,2007, 30: 231–235

5 成雨. 层析 γ扫描技术效率矩阵刻度模型研究. 上海:上海交通大学机械与动力工程学院, 2007 CHENG Yu. Study On The Scale Model Of Efficiency Matrix Of Tomographic Gamma Scanning. Shanghai:School of Mechanical Engineering Shanghai Jiao Tong University, 2007

6 Vidmar T, Korum M, Likar A, et al. Nucl Instr Meth Phys A, 2001, 470: 533–547

7 张斌全, 马吉增, 程建平, 等. 核电子学与探测技术,2005, 25: 274–277 ZHANG Binquan, MA Jizeng, CHENG Jianping, et al.Nuclear Electronics & Detection Technology, 2005, 25:274–277