城市轨道交通整流机组几个参数的分析与计算

于 波，周才发

0 概述

目前，国内各大城市大力发展的城市轨道交通供电系统，其牵引整流系统大多采用2套12脉波整流机组并联运行，构成等效24脉波整流。同一组12脉波整流器中的2个三相全桥整流器的输入三相交流电压相位差为30°，每个三相全桥整流器将输入的三相交流电压变换成6脉波的直流电压，并联输出后成为12脉波整流电压，2个12脉波整流器再并联后最终形成24脉波直流电压。

1 理想空载整流系数与整流脉波数的关系

各种脉波整流电压波形如图1、图2所示。

从图中可以看出，对于12脉波整流，在推挽工况下，整流后的波形为一个正弦波周期内有 12个相同的波纹，此时波纹周期为π/6。得出12脉波的理想空载电压有效值

同理 24脉波的理想空载电压有效值Udi=1.41U2e。

2 额定空载整流系数与整流脉波数的关系

当直流负载电流大于拐点（临界）电流时，2组三相桥臂由推挽工况（任何时刻只有相当于一个桥臂导电，对于12脉波整流有6个桥臂）转化为完全并联工况（任何时刻2组三相桥臂中，各有一个桥臂同时导电）。

图1 12脉波电压波形图

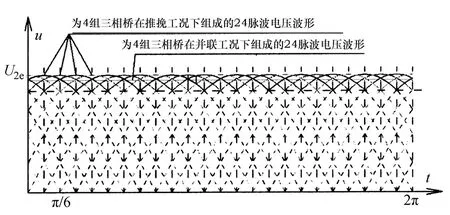
图2 24脉波电压波形图

利用整流变压器二次侧漏抗或者接入平衡电抗器 LP后，当直流负载电流大于拐点（临界）电流后，任意时刻平衡电抗器上的电压为图3中两波形的差值。LP产生的感应电压使两导电支路线间电压相等，即使整流电压ud相等。则ud= (u1+u2)/2。

从图 3可假设 1组三相桥臂波形为u1=另1组三相桥臂波形为u2=

因此，12脉波额定空载电压有效值为0.965 9×1.398U2e= 1.35U2e。

图3 整流电压与平衡电抗器电压波形图

同理可以推出24脉波整流时，额定空载电压有效值也为1.35U2e。

从上面分析可知：当直流负载电流大于拐点（临界）电流后，无论是12脉波整流还是24脉波整流，额定空载电压都是1.35U2e。

3 牵引整流变压器阀侧与网侧容量的关系

12脉波整流时，变压器2组阀侧均为桥式全波整流，在忽略换相时的重叠角，且负载为电感性负载等理想条件下，阀侧2组绕组总的交流等效容量为

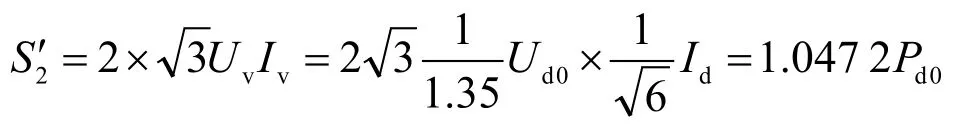
因为2组阀侧中除γ=kp±1（k= 1，2，…）特征谐波外的其他高次谐波都相互抵消了，所以网侧绕组的交流等效容量为

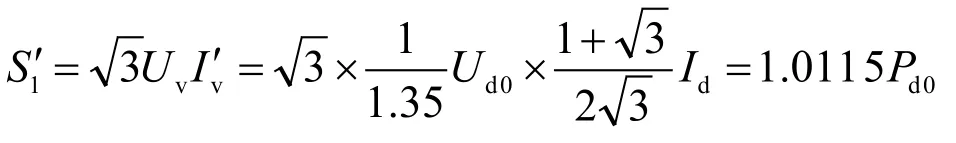
考虑到额定运行时系统的电压降为额定直流电压的6%左右，因此变压器的等效交流容量为

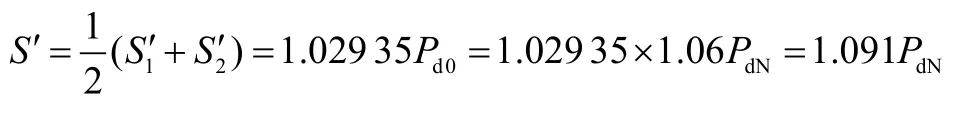
故变压器的额定容量一般为直流额定功率的1.1倍。

在24脉波整流中，工程上计算电流时，可以近似按12脉波整流计算。

4 整流变压器阀侧电压的选取

当35 kV交流电压波动与24脉波整流电路网压波动时，各整流变压器电压比值对应的理想直流空载电压见表1。

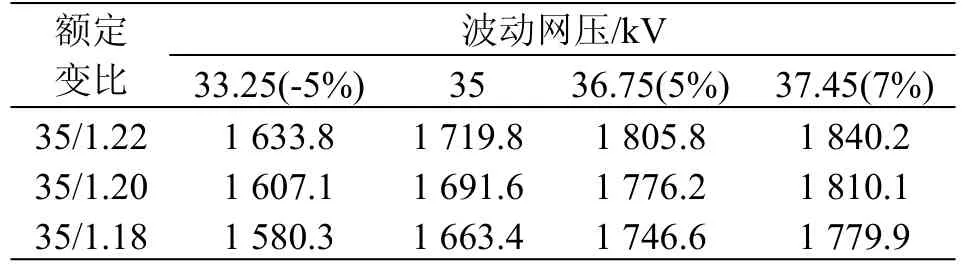
表1 网压波动时24脉波整流电路空载电压表 单位：V

从表1中可知，若按照35 kV系统电压正负偏差最小为5%，整流变压变比为35/1.22时，空载电压已经超出了牵引系统允许电压最高值1 800 V，由于整流器直流空载电压过高还将影响车辆电力制动功能。考虑到国家规范中对35 kV电压的允许偏差的规定：“35 kV及以上供电电压正、负偏差的绝对值之和不超过额定电压的10%”，35 kV电压的正偏差可能高于5%，达到7%。所以建议地铁中的整流变压器二次侧电压选1.18 kV。这个结论符合国内整流变压器变比为35/1.22或35/1.20地铁线路运营中，网压有时偏高的事实。

5 额定直流电压调整率的计算

按照国家标准的定义，直流电压调整率是额定空载直流电压Udo与额定直流电压Ude之差对理想空载直流电压Udi为基准的相对值。

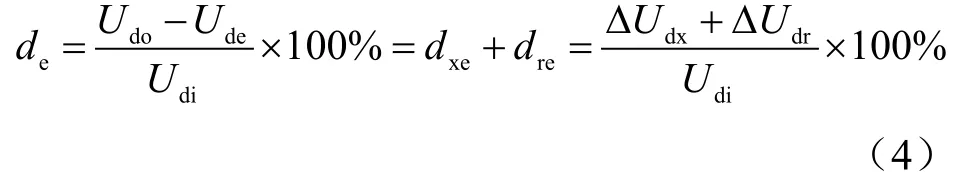
式中，Udo为额定空载直流电压，dxe是由整流变压器换相电抗产生的电压调整率。dre是电阻压降电压调整率，即包括变压器铜损、整流二极管正向功耗及连接电缆等压降产生的电压调整率。

按照国家标准定义有

式中，S为串联换相组组数；q为换相数；Xh为换相阻抗（转化为二次侧的电抗）；g为分流Ide的换相组的组数（S= 2，q= 3，g= 2）。

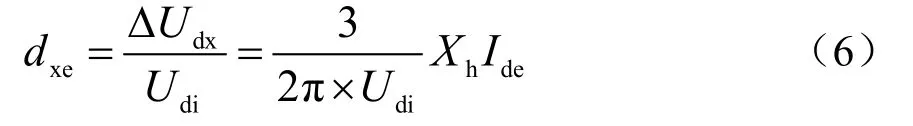
其中Ide为负载电流，对于24脉波整流则是2套整流机组的直流负载电流。

dxe也可以用标么值表示：

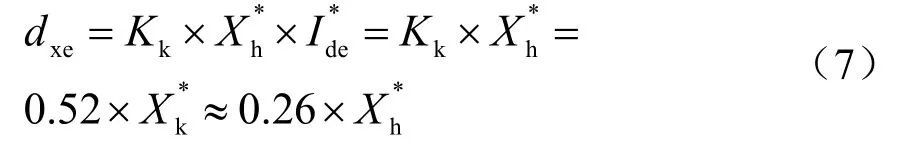
鉴于希望因变压器换相引起的直流电压调整率低些，这样可以提高整流装置的效率，但由式（7）知道，这样会降低穿越阻抗，影响变压器的抗短路能力。综合起来考虑，对于轴向分裂式牵引整流变压器，穿越阻抗取7%～8.5%（标么值），则直流电压调整率dxe取 3.64%～4.42%，建议穿越阻抗取8%（标么值）为佳，于是dxe为4.16%。实际的牵引整流系统的直流电压调整率尚需考虑整流元件压降、低压引线漏抗、连接电缆及变压器本身的电阻压降等，所以对整个整流系统来说，直流电压调整率约为6%。

其中Pk为整流机组试验短路损耗（含整流元件损耗）；SN为整流变压器容量。

由以上公式可以算出额定直流电压调整率。

6 直流负载拐点（临界）电流

6.1 直流负载拐点（临界）电流的意义

图4是整流机组的负载特性曲线，以12脉波为例，只有当负载电流大于拐点 G处的拐点电流时，2组三相桥臂并联才能同时输出，在拐点前，2组三相桥臂处于推挽工作状态。

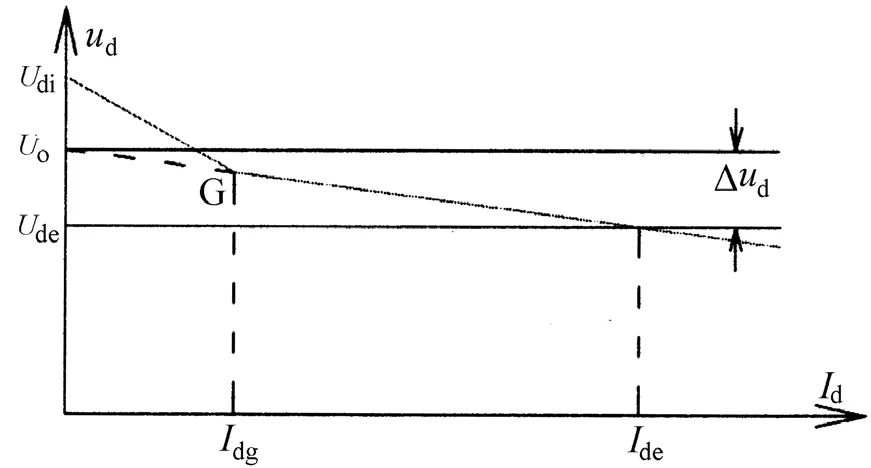
图4 整流负载特性曲线图

所以，在拐点前区域工作有如下缺点：输出波形尽管是12脉波，但是电压平均值突升较高；整流机组效率稍低；交直流侧谐波含量也有所增加，由于在拐点前整流在推挽状态，每一时刻只有一组回路（每组回路是2个桥臂串联）导通，则每个桥臂必须承受此时的负载电流（瞬时值），在拐点后整流，对于12脉波，每一时刻是2组回路并联导通，则每个桥臂承受此时负载电流（瞬时值）的一半；对于24脉波，每一时刻是4组回路并联导通，则每个桥臂承受此时负载电流（瞬时值）的1/4，所以应尽量减小临界电流，这样可以提高二极管的利用率，增加二极管的寿命。

为使临界电流不至于太大，对于取消平衡电抗器的2组三相桥臂并联，在整流变压器设计选取参数时，必须尽量增加整流变压器二次侧绕组的漏抗即增加二次侧绕组的短路电抗。

6.2 均衡电压

12脉波整流变压器二次侧的 Y绕组和Δ绕组线电压有效值相等，但2个绕组的线电压相位差为30°，其瞬时值是不相等的。该瞬时电压差被称为均衡电压。

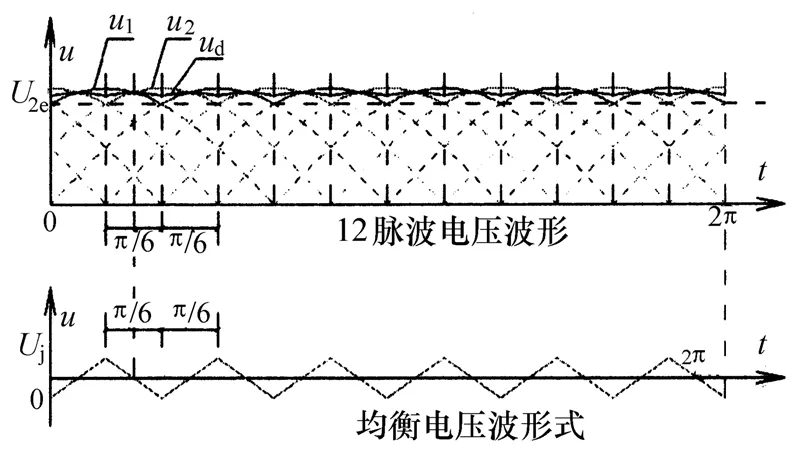
图5 整流电压与均衡电压波形图

从图5可看出均衡电压uj周期为π/3。以均衡电压过零时为时间零点，当ωt在-15°～+15°之间时，一组三相桥波形为另一组三相桥波形为则有：

同理，当ωt在15°～+45°之间时，有

均衡电压有效值可以表示为

最大均衡电压

6.3 均衡电流

均衡电流有效值则为Ij=Uj/Xj=Uj/ 6Xf

Xf为整流变压器二次侧分裂电抗，均衡电抗Xj= 6Xf（因为12脉波中，并联运行的2个换相组件中的整流臂每换相一次均衡电流就改变一次方向，由于每个桥臂每相串联换相组数为2，因此均衡电流基波频率是电源基波频率的6倍。）

6.4 2个换相组的负载电流

2个换相组的负载为

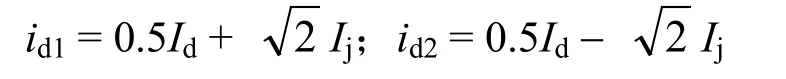
由于二极管的单向导电性，因此2组三相桥并联同时输出必须满足id2＞0，即由此可以得出拐点电流计算公式

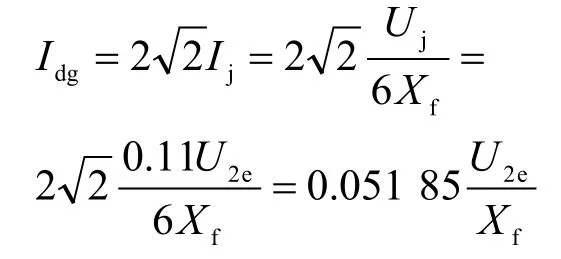
也可以推出

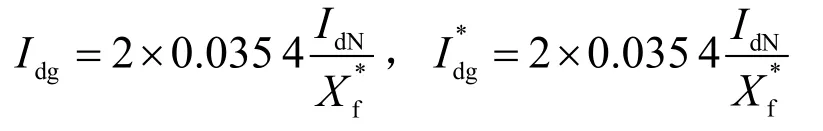
IdN为单台整流器输出的额定直流电流。

对于相同短路阻抗和分裂系数的牵引整流变压器，因为整流变压器的耦合系数很小，所以4桥并联24脉波系统的临界负载电流几乎是2桥并联12脉波系统的临界负载电流的2倍。由于24脉波整流是2套整流机组，所以单台整流机组的临界电流基本等于但略小于一套12脉波整流机组的临界电流。

6.5 临界电流的计算

例如：对于2 500 kV·A整流变压器，制造厂提供的感抗参数（折算到10 kV侧）为原边X1=1.45 Ω，次边X2= 3.61 Ω，X3= 3.63 Ω（计算时取X2=X3= 3.62 Ω）。

整流器额定电流为3 000 A。

则临界（拐点）电流Idg与额定电流Ide的比值为1 173.5 / 3 000 = 39.2%。

6.6 对临界电流计算结果的思考

牵引整流变压器短路阻抗Xk=X1+ 0.5X2；换相阻抗Xh=X1+X2；耦合系数Kc=X1/Xh，分裂阻抗Xf=X2+X3；分裂系数Kf=Xf/Xk。

对于分裂式牵引整流变压器，一般Kf取 3～3.4；按一般厂家的设计制造水平，取Kc= 0.1。

被试整流变压器的Kc及Kf值：Kc=X1/（X1+X2）= 0.286（大于0.1）；分裂系数Kf=Xf/Xk= 2.22（不在3～3.4之间），如果将Kc及Kf控制在规定范围内，则临界（拐点）电流与额定电流的比值会更小。

短路阻抗不变的情况下，耦合系数越小，分裂系数就越大，则分裂阻抗越大，这样临界（拐点）电流就越小。

分裂系数相同，穿越阻抗越小，则分裂阻抗也相应变小，这样临界（拐点）电流就变大。

7 结束语

本文针对城市轨道交通整流机组一些重要参数的选取和计算方法进行了分析探讨和总结，希望能对解决工程设计中的实际问题和积累城市轨道交通的设计经验、提高工程质量有一定参考价值。

[1]王念同，魏雪亮.轴向双分裂式12脉波牵引整流变压器均衡电流的分析计算[J].变压器，2000，（3-4）.

[2]丁光发，刘臻，余梦华.对整流机组联调试验若干问题的分析[J].都市快轨交通，2004，（6）.

[3]GB/T3859-93 半导体变流器应用导则[S].

[4]中铁二院工程集团有限责任公司.杭州地铁1号线初步设计文件[R].杭州，2008.