带p-Laplacian算子时滞微分方程边值问题多个正解的存在性

丁卫平

(湖南理工学院 数学学院, 湖南 岳阳 414006)

带p-Laplacian算子时滞微分方程边值问题多个正解的存在性

丁卫平

(湖南理工学院 数学学院, 湖南 岳阳 414006)

应用锥上不动点定理, 研究具有p-Laplacian算子边值问题

边值问题; 锥; 不动点定理; p-Laplacian算子; 正解

引言

边值问题一直受到不少学者关注. 文[1]研究了Sturm-Liouville边值问题

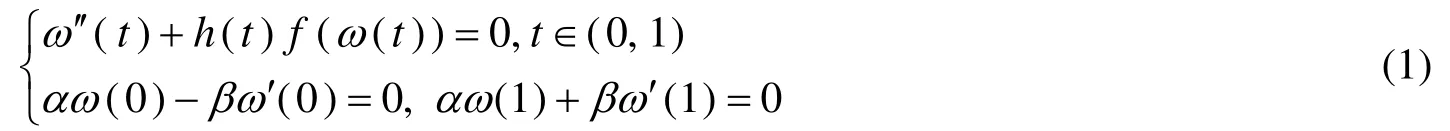
并给出了边值问题(1)有n个对称正解的存在性证明; 文[2]研究了如下

的边值问题, 推广了有关结果; 文[3]研究了边值问题并采用了锥上的不动点定理给出了(2)存在三个正解的充分条件. 本文将采用不同于文[1]～[3]的方法研究时滞两点边值问题

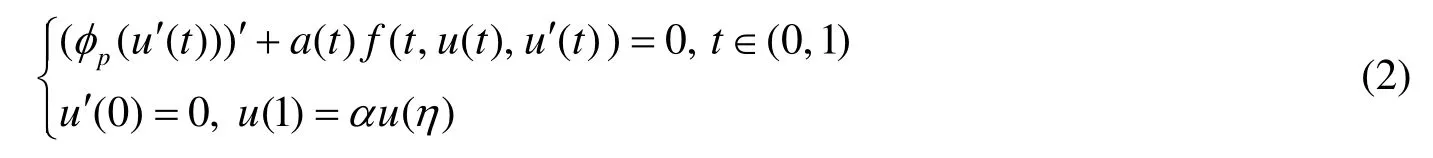
1 主要结果

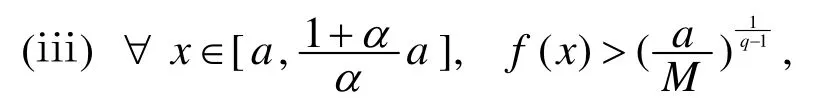
则边值问题(3)至少有两个正解.

2 主要结果的证明

2.1 定理1的证明

因此, 根据引理1, 边值问题(3)至少有三个正解.

2.2 定理2的证明

[1] Yao Q.Existence and iteration of n symmetric positive solutions for a singular two-point boundary value problem[J]. Compute. Appl., 2004, 47: 1195～1200

[2] 蒋达清, 张丽莉. 二阶时滞微分方程边值问题的正解[J]. 数学学报, 2003, 46(4): 739～746

[3] 杜 波, 葛渭高. 一类具p-Laplacian算子边值问题三个正解的存在性[J]. 数学的实践与认识, 2008, 38(20): 201～204

[4] 郭大钧. 非线性泛函分析[M]. 济南: 山东科学技术出版社, 2001

Existence of Multiple Positive Solutions of Boundary Value Problems with p-Laplacian Delay Differential Equation

DING Wei-ping
(College of Mathematics, Hunan Institute of Science and Technology, Yueyang 414006, China)

By using a fixed point theory in cones, the paper studies the existence of positive solution for the two-point boundary-values problem

boundary value problem; cone; fixed point theorem; p-Laplacian operator; positive solution

O175.8

A

1672-5298(2010)03-0017-04

2010-04-03

丁卫平(1964- ), 男, 湖南岳阳人, 硕士, 湖南理工学院数学学院副教授. 主要研究方向: 信息论及应用