基于FPGA的直线插补器的研究与设计

上海交通大学电子信息与电气工程学院（上海200240） 陆 悦 张 峰 贺 超

1 引言

运动控制技术发展至今，从实现上可以分为软件实现和硬件实现两种。硬件实现以往多依赖于ASIC芯片设计，使得普通工程技术人员很难参与其中，因此，市面上流行很多经济型的单片机或者DSP软插补器。由于计算速度上的限制以及软插补器自身的缺陷，这些插补器很难做到高精度和多轴联动。随着EDA技术的发展，可编程逻辑器件的出现打破了这样的格局。特别是工艺的进步使得FPGA价格不断下降，也使其更加适合运动控制场合。本文即研究如何利用FPGA完成对步进电机的直线运动控制。

2 DDA算法的选择与原理

目前比较成熟的数控插补算法有逐点比较法、最小偏差法和数字积分法等，DDA（数字积分法）利用数字积分的方法，计算刀具沿各坐标轴的位移，使得刀具沿着所加工的曲线运动。DDA插补算法具有运算速度快、脉冲分配均匀、易于实现多坐标联动等特点，在轮廓控制数控系统中有着广泛的应用[1]。本文即采用DDA算法实现直线插补。

数字积分的原理是将函数的积分运算转换成变量的求和运算。如果所选择的脉冲当量足够小，则用求和运算代替积分所引起的误差可以不超过允许的数值。这样，可以采用两个寄存器（函数寄存器和累加寄存器）和一个全加器构成数字积分器[2]。将单位周期选的足够小，每单位周期都向累加器累加函数寄存器中的数值，如果累加器溢出，就向外发送脉冲，实时的改变函数寄存器的值，就可以完成电机的调速。

3 插补器的设计与实现

图1为整个插补器的框图，其中比较重要的是预判模块、梯形模块和S型模块。

3.1 核心内容设计

3.1.1 输入参数

输入部分是初始数据的接口，可以设计成各种接口从外部接受数据，比如SRAM时序、PCI接口等等，这不是本文讨论的内容。该部分比较重要的是接收哪些数据，在设计中，对于每条直线需要初始速度、最高速度、加速时间、运动距离、X轴Y轴距离比例和运动类型这几个参数。初始速度控制电机运动的起始速度，最高速度决定运动过程中的最高速度，加速时间控制加减速过程的时间，运动距离是电机运动的总距离，X轴和Y轴距离比例用来使X轴和Y轴脉冲均匀分配，运动类型决定加减速控制的类型。

另外一个需要注意的问题是，在FPGA内部所有数据都是整形的，而实际参数可能是带小数的，对此的处理是左移规格化，将参数在输入FPGA之前做一定的预处理，将距离单位转换成脉冲个数，时间单位转换成每单位周期，并放大统一的倍数，最终单位为累计量每周期。例如，初始速度为0.1mm/s，脉冲当量为0.0001mm，积分周期为100ns，左移32位，则规格化之后的初始速度为：

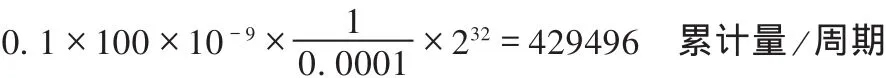
其他变量做类似处理。

3.1.2 加减速控制

控制电机做直线运动最复杂的就是电机的加减速控制，为了防止电机失步，不能直接发送给定频率的脉冲，需要有加速和减速的过程。加减速控制有两种方法，梯形方法和S型方法。如图2所示，梯形方法是采用恒定加速度，S型方法是采用变加速度和恒定加加速度的2次加速方案。

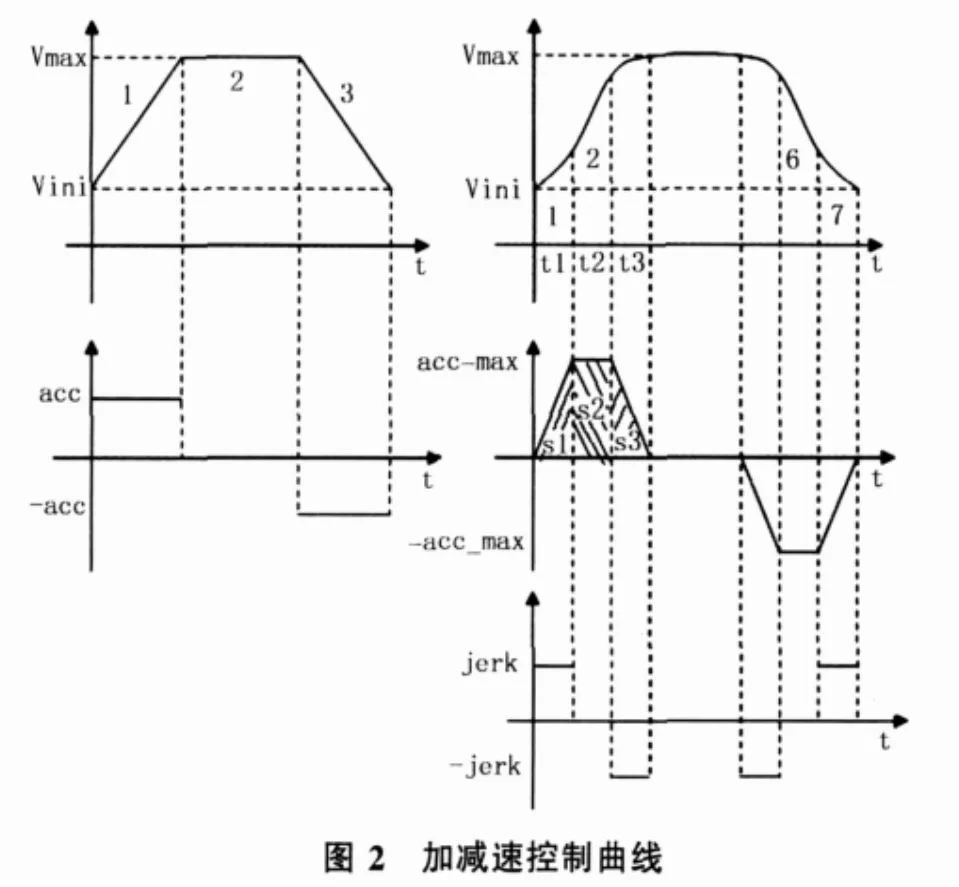
由于运动距离的限制，有可能会发生加速不到最高速度就需要减速的情况。如图3所示。

从图2中根据加速过程中的对称关系可以证明，在初速度和最高速度相同的情况下采用梯形加速和S型加速方式，加速过程运动的距离相等。因此，两种方法都可以按照梯形方式来计算给定路程下能达到的实际最高速度。

在电机控制过程中，按照加速度变化规律去改变上文提到的函数累加器的值就可以实现调速。不同的是，梯形方式中加速度是个恒定值，而S型方式中，加速度也需要根据加加速度来不断调整。用加加速度调整加速度的方式和用加速度调整速度的方式相同。

为了能够使调速均匀平滑，本算法中采用了以空间矢量为长轴的方式[3]。按照X轴和Y轴的比例，将脉冲均匀地分配到两轴。

3.1.3 分界点的判断

图2表明，在加减速过程中有不同的阶段，因此带来了阶段分界点判定的问题。梯形方式，分界点比较简单，1和2阶段的分界点按照最高速度值判断即可，即一直按照给定加速度加速，直到速度达到最大值。2和3阶段的分界点则可以根据到该点时的路程值来判定，由于加速和减速过程对称，两个过程运动距离相等，总距离减去加速运动距离就是该点处的距离值。由于最终使用的速度最大值是计算得到的实际最大值，因此不会出现达不到最大值的情况。

S型方式的分界点比较复杂，本文提供了一种很好的简化实现。之前提到，两种方式在加减速过程按照相同的方法计算实际最大速度，在最大值确定之后，可以按照一定比例设计S型方式中各个阶段的时间比例，并根据此比例获得分界点的速度值。例如图2 所示，假设 t1∶t2∶t3=1∶1∶1，则面积比 s1∶s2∶s3=1∶2∶1，这样三个阶段的速度增加值可以通过这个比例计算得到，而且比例数字避开了除法。计算得到恒定加加速度阶段（图2S型方式2阶段）的速度变化值之后，就可以计算得到加加速度的值，这样只要按照加加速度去控制3个阶段就完成了S型加速过程分界点的控制。减速点的处理与梯形方式相同，减速过程与加速过程类似。

3.1.4 距离的累加

本文算法采用100ns作为插补周期，使得不论是梯形方式还是S型方式，在处理距离的累加时，都可以将运动过程看作是恒定加速度的运动。这样根据运动学公式，由于速度单位是累计量每周期，所以累加值应该为：

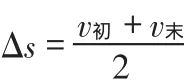
按照该公式，只需要计算每个插补周期开始速度和末速度之和，然后右移1位作为距离累加值即可，这样还避开了除法运算。

3.2 模块介绍与程序框图

在讨论完算法的核心内容后，我们在此基础来看各模块的功能和程序框图。

3.2.1 预判模块

该模块实现实际最大值的计算和分界点的计算功能，程序框图如图4所示：

3.2.2 梯形模块

该模块利用预判模块的数据，在使能后按照梯形方式发送脉冲。程序用状态机实现，时钟频率为50MHz，每个时钟周期20ns，通过两组5种状态的状态机的转换可完成梯形方式控制。程序框图如下所示：

3.2.3 S型模块

该模块利用预判模块的数据，在使能后按照S型方式发送脉冲。与梯形方式相比也是使用状态机来实现，但是增加了加加速度的控制，状态转换也更为复杂。程序框图如图6中所示：

4 仿真与实验结果

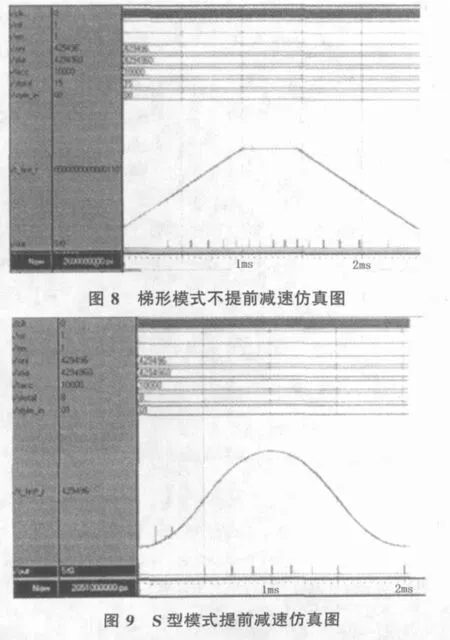
用quartus2进行综合后，用ModelSim仿真结果如下：

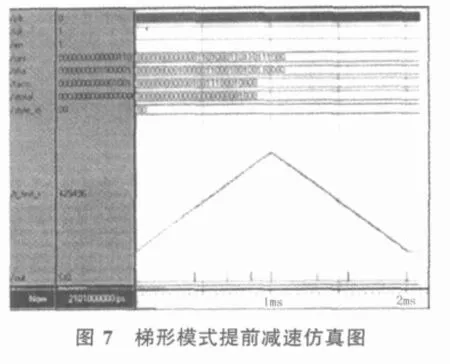
以上仿真结果，是采用两种不同方式在相同的数据下的仿真得到的数据。图中曲线是将函数寄存器中的数值设置成模拟 （analog）方式观察得到的，这些曲线表示了速度值的变化，曲线下方是发出的脉冲电平，横轴是时间，单位是毫秒。为了重点表现加减速过程，仿真是对单轴的控制，脉冲即是发出的控制脉冲。距离充足的一组数据是：加减速时间1ms，路程15个脉冲，初速度0.1mm/s，末速度1mm/s，脉冲当量0.0001mm；距离不足的一组数据中除路程是8个脉冲外，其他与以上相同。仿真结果，完全正确。

在实践中，采用 Altera公司的ep1c12，实验得到，利用梯形加速，电机从速度0加速到频率200k，加速时间最短在0.4秒左右，而用S型可以在不到0.1秒内成功启动。

5 结束语

本文阐述了采用FPGA实现DDA直线插补器的一种思路，并重点讨论了加减速的控制等核心内容。仿真和实践都证明了其正确性。下一步需要完善的是如何动态改变运动参数，这对于实际应用也非常重要。

[1]闫华，汪木兰，王保升.基于FPGA的最小偏差法插补器是设计与实现[J].机械设计与制造，2008（12）：14 ～ 16.

[2]李恩林著.数控系统插补原理通论[M].北京:国防工业出版社，2008.

[3]蒋志冬，丁庆生.基于FPGA实现的多轴数控雕刻机系统[J].机电产品开发与创新，2006（1）:129 ～ 131.

[4]Samir Palnitkar著，夏宇闻，胡燕祥，刁岚松等译.Verilog HDL数字设计与综合[M].北京:电子工业出版社，2004.

[5]王诚，吴继华，范丽珍，薛宁，薛小刚著.Altera FPGA/CPLD设计[M].北京:人民邮电出版社，2005.