LDPC码在 AWGN信道中的性能研究

邵丽娜,史 萍,骆 超

(中国传媒大学 信息工程学院,北京 100024)

1 引言

伴随着通信技术的飞速发展以及各种传输方式对可靠性要求的不断提高,差错控制编码技术作为抗干扰技术的一种重要手段,在数字通信领域和数字传输系统中显示出越来越重要的作用。自从Shannon提出信道编码定理[1]以来,编码研究者们一直致力于寻找性能上尽可能接近 Shannon极限而复杂度又较低的信道编码方案。可惜的是,从上世纪 50年代以来研究的传统纠错码都不是实用好码[2]。1993年,Berrou等人提出的 Turbo码[3]通过采用软输出迭代译码来逼近最大似然译码,取得了超乎寻常的优异性能,被看作信道编码理论研究的重要里程碑。在对 Turbo码的基于图模型的编译码和迭代译码研究过程中,David J.C.Mackay,M.Neal和 N.Wiberg等人发现[4],早在 1962年 Robert G.Gallager提出的低密度奇偶校验码[5](Low Density Parity Check Codes,LDPC Codes)也是一种实用好码,其在 AWGN信道下的性能接近 Shannon极限且实现复杂度低。1996年 Mackay教授等人重新发现了 LDPC码后,便轰动了编码界,成为自信息论提出以来最重大的研究进展之一。理论研究表明:1/2码率的 LDPC码在 BPSK调制下的性能距信息论中的 Shannon限仅差 0.0045dB[6],是目前距 Shannon限最近的纠错码。LDPC码与高效调制相结合,能够满足下一代移动通信高速数据大容量传输的迫切要求,它的迭代译码思想现已广泛用于通信技术的很多领域,为实现迭代信道估计、迭代均衡以及信号检测提供了新的思路。

2 LDPC码编码原理

对 LDPC码编码方法的研究主要分两步进行,首先是奇偶校验矩阵的构造,然后是基于奇偶校验矩阵的编码算法。

2.1 码字构造

LDPC码校验矩阵的构造方法可分为两大类:一类是随机构造法,其校验矩阵不规则,虽然纠错性能好,但由于校验矩阵的随机性使得编码复杂度高。下文中介绍的Gallager构造法和PEG构造法属于此类;另一类是结构化构造法,它由几何、代数和组合设计等方法构造,其校验矩阵具有某种特殊的结构,因而其硬件实现比随机结构的码容易,而且可以通过设计 girth较大的码,使其性能达到随机校验矩阵生成的码字,下文中介绍的准循环构造法即属于此类。

2.1.1 Gallager构造法

Gallager构造的 LDPC码[7]具有如下特点:校验矩阵 H的列重和行重固定,且列重 dv≥3;H中的元素随机生成,行重和列重均匀分布;矩阵按行划分成dv个水平子矩阵,子矩阵中每列只有一个“1”,第一个子矩阵中第 i行只有从第(i-1)dc+1列到第 idc列的元素为“1”,其余子矩阵是第一个子矩阵的随机列变换。该类码的码集合是由H中下面dv-1个子矩阵的列等概率随机分配所得码的集合。Gallager方法构造的码字对于给定列重 dv,对足够低的信噪比和足够长的码长,最佳译码器的错误概率随码长指数下降;码的最小距离随码长线性增加。

此种方法下,校验矩阵构造简单,而且校验矩阵的行重列重容易控制,只需先根据码长和行重构造一个子矩阵,校验矩阵就可以利用此子矩阵得到。但是由于是随机构造的原因,在码长较短时 Tanner图中经常容易出现短环,影响了码的性能,但是随着码长的增加,短环出现的概率会变小。

2.1.2 PEG构造法

Xiao-Yu Hu提出了一种使得变量节点的局部围长最大的构造方法,即 PEG(progressive edge grown)方法[8],PEG方法构造的中、短码长的 LDPC码是当前所知具有相同参数的最好的低密度奇偶校验码之一[8]。

PEG算法是构造具有大环 Tanner图的一种次优方法,算法在图上每增加节点的一条边都使得该节点局部环长最大。假如已构造图 G′中 j个节点的边集合为 Ev0∪Ev1∪ …Evj-1,g′是图 G′的围长,g′=min{gv0,gv1,…ggvj-1},若在图中增加 Evj,使新得到的图的最小环小于 g′,那么这个新产生的最小环必须通过点 Vj,构造最大围长 Tanner图就是优化Evj中dvj条边,使该节点的局部环长最大。

由于短环的存在对译码性能存在很大的影响,利用 PEG方法构造的校验矩阵使得最小环长最大,因而一般来说,利用 PEG方法构造的校验矩阵比利用 Gallager等方法构造的校验矩阵性能好。但此种方法要对边的分布进行优化,其复杂度随之增加。

2.1.3 准循环构造方法

准循环的 LDPC码的校验矩阵 H由一系列的 m×m小循环方阵组成[9][10],这些小循环方阵可以是置换矩阵或是基于有限几何的矩阵等。

式(1)中 p代表 m×m单位阵,上标 a表示平移的数。选用不同的 a可形成不同的编码方法。由于准循环码的准循环特性,可以得到系统形式又具有准循环特性的生成矩阵,只需要采用移位寄存器即可实现输入码字和生成矩阵的相乘。

准循环 LDPC码具有循环码的一些特性,也可以采用一维寄存器完成编码,硬件实现复杂度低。在标准 CCSDS131.1-0-2(EX-PERIMENTAL SPECIFICATION)[11]中针对近地业务和深空业务提出的 LDPC码方案都是准循环 LDPC码,由此也可见其良好的应用前景。

2.2 编码算法

在传统的编码过程中,一般生成矩阵是必需的。然而针对 LDPC编码,尽管码字的奇偶校验矩阵是非常稀疏的,但其生成矩阵的稀疏性却无法保证,这样就可能会导致编码的运算和存储复杂性大大增加,不具有实用性,因此出现了一些新的编码方法,不再产生生成矩阵,直接利用校验矩阵进行编码,以期获得较低的编码复杂度。下面就主要介绍一种使用比较广泛的 RU算法。

Richardson和 Urbanke在文献[12]中提出的RU算法通过行列置换将一般的低密度奇偶校验矩阵化为一个近似下三角矩阵(图 1),可以使编码复杂度从高斯消元法的 o(m2)降为 o(n+g2),其中 g为近似下三角矩阵与下三角矩阵的差距,并且在最恶劣的情况下,它只是与码长的一小部分成比例。

图 1 奇偶校验矩阵的近似下三角形式

由于原矩阵 H非常稀疏,而且在矩阵变换中只有行列交换,因此变换后得到的近似下三角矩阵仍然是稀疏矩阵。长度为 k的信源向量 s被编码成一个码字向量 x=(s,p1,p2),其中 s代表系统比特。p1与 p2代表校验比特,长度分别为 g和 m-g。通过式(2)可以分别递推出两部分校验比特[12]。

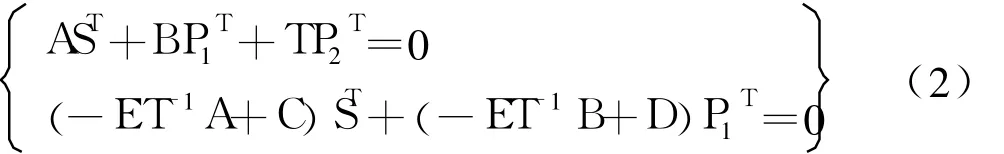
这六个分块阵是通过对原有稀疏矩阵的行列做重排获得的,所以这些分块阵依然满足稀疏性,通过进一步的分析即可得到和的运算量分别为和。由此可以看出,要进一步简化 LDPC码的编码运算量,需要在重排校验矩阵的时候使得尽量小,运算量就可以控制在线性复杂度附近。

3 LDPC码译码原理

LDPC码具有良好性能的重要原因之一是:LDPC码采用了基于置信传播的迭代译码算法,这是一种迭代概率译码方法,是 LDPC码与传统纠错码的重要区别所在。另外,Gallager在 1962年的文章中还提出了一种基于置信传播的硬判决翻转译码算法。下面分别介绍基于置信传播的迭代概率译码方法和位翻转译码方法。

3.1 BP译码

基于因子图的置信传播译码算法(BP Algorithm)是 LDPC码常用的译码算法。对于二元LDPC码的译码,信道模型采用二元输入连续输出平稳无记忆 AWGN信道模型,假设采用 BPSK调制方式,噪声服从高斯分布 N(0,)。设一个 N长LDPC码的校验矩阵 H=(Hij)M×N,码字 X={…xN}表示为一组信息节点,Z={z1,z2,…,zM}表示为一组校验节点,观测的信道信息给出关于发送码字的初始化信息向量 ƒa={…,}。用 M(j)表示与变量节点 xj相连的所有校验节点所构成的集合,相对应于校验矩阵 H中第 j列为 1的位置,用 N(i)表示与校验节点 zi相连的所有变量节点构成的集合,相对应于校验矩阵 H中第 i行为 1的位置。M(j)i表示 m(j)中除去其中的校验节点 zi后剩下的集合,N(i)j表示 N(i)中除去其中的变量节点 xj后剩下的集合。校验节点 zi向变量节点 xj传递的校验信息定义为变量节点 xj向校验节点 zi传递的变量消息定义为

图 2显示了校验信息和变量消息的传递方向,基于因子图模型和和积算法,置信传播算法执行的操作如下:

2.迭代消息传递和修正;

(1)各因子节点 fj向其父节点 xj传递消息校验节点 zi向其所有父节点 xj分别传递消息,各节点 xj根据接收消息修正

(2)各变量节点 xj向其所有子节点 zi传递已更新的消息各节点 zi根据接收消息修正

图 2 置信传播算法示意图

4.迭代或终止:计算 xHT是否为全零向量。如果是,则本次译码结束;若不是,判断是否达到最大迭代次数。如果已达到最大迭代次数,结束译码,以最后的结果作为输出;若没有达到最大迭代次数,则进入下一次迭代,直到满足 xHT为零为止。

3.2 硬判决位翻转译码

比特翻转译码方法由 Gallager教授在其论文中首先提出,这种算法仅适用于 BSC信道,可看成是置信传播算法的简化形式。设码字向量经过 BSC信道接收的硬判决值为 z,s为伴随子向量,比特翻转(BF)算法可简单描述为:

1.首先计算方程 s=zHT,统计每位接收值 yi不满足校验方程的个数。

2.找出不满足校验方程的个数最多的 zj,如不满足的个数大于某设定值,将其翻转,得到新的向量 z′。

3.判决条件:由向量 z′代替 z计算方程 s=zHT,如 s=0则正确译码输出,否则重复第 1-3步。反复迭代,直到迭代至最大迭代次数。

由于校验矩阵为稀疏矩阵,而且一般为随机构成,所以参与每个校验方程的比特很少,且这些比特在码字上分布很分散,那么任意一个校验方程所含的比特要么无错,要么以很高的概率只发生一个比特的错误,因此 BF算法就可以有效的进行纠错。

4 LDPC码在 AWGN信道中的仿真实验

4.1 仿真模型

实验采用二进制的伪随机序列作为输入信号,帧长为 4608比特。LDPC编码中的校验矩阵采用CMMB标准[13]中的规则校验矩阵 H(9216,3,6),码长为 9216,行重为固定值 6,列重为固定值 3。经过LDPC编码后的信号再进行 BPSK调制,然后进入高斯白噪声信道。信道的输出信号首先进行 BPSK解调,然后进行 LDPC信道译码,采用和积译码算法,译码后的结果进行判决并统计误码率。图 3为实验采用的仿真模型。

4.2 仿真结果

4.2.1 LDPC码和 Turbo码在 AWGN信道中的性能比较

图 4给出了 LDPC码和 Turbo码在 AWGN信道中的仿真性能曲线图。实验在 CPU为 Intel core2 E7300,主频 2.66GHz,内存为 2.00GB的计算机上用 C语言编程完成,其中 LDPC码的校验矩阵采用CMMB标准中的规则校验矩阵 H(9216,3,6),码率1/2,译码采用 BP译码算法;Turbo码的码率为 1/2,译码算法采用 MAP译码算法[14]。

图 3 LDPC码在AWGN信道中的信真模型

由仿真结果我们看到在信噪比较低的时候,Turbo码的性能比 LDPC码的性能好很多,可是当信噪比增大后,尤其是在信噪比达到 1.5dB以后,Turbo码的性能呈现错误平层,出现无法纠正的错误,而 LDPC码在信噪比到 1.5dB以后误码率下降非常快,从仿真 10000次的时候来看,在信噪比达到1.6dB时几乎已经完全纠正错误,表现了优良的纠错性能;另一方面,在本实验采用 BP基本译码算法的情况下,LDPC码的译码速度远远大于 Turbo码的译码速度。由仿真结果我们看到当采用 LDPC码作为信道编码方案时,译码采用 10次迭代仿真的时间大概只是 Turbo码仿真时间的 1/2,即使是 LDPC码译码采用 30次迭代的仿真时间也要比 Turbo码作为信道编码译码迭代 10次的时间短很多,这反映了LDPC的译码速率比 Turbo码高,译码的复杂度低于Turbo码的译码复杂度。

图 4 LDPC码与 Turbo码在 AWGN信道中的性能曲线图

4.2.2 译码迭代次数对 LDPC码性能的影响。

图 5给出了当译码迭代次数不同时,同样的LDPC码字在 AWGN信道中的性能曲线。由仿真结果我们清楚地看到随着迭代次数的增加,曲线的趋势也表现出越来越好的性能;同时,随着迭代次数的增加,从仿真所需要的时间来看,译码所需的时间也在增加。可以看出通过迭代次数来提高 LDPC编码的误码性能是以译码速率为代价的,所以在选择适合的迭代次数的时候我们要综合实际需要寻找一个性能和速率的平衡点。

5 结论

LDPC码这种新颖的信道纠错编码技术,继Turbo码之后向逼近 Shannon限的目标又跨进了一步。从本文的实验当中我们可以总结出以下结论:在信噪比较大时,LDPC码的性能要优于 Turbo码,并且其译码速率要高于 Turbo码;译码迭代次数是影响 LDPC码译码性能的一个重要因素,增加译码迭代次数可以提高译码性能,但同时复杂度消耗也在增大,所以采用 LDPC码作为信道编码的时候我们要综合实际情况选择合适的译码迭代次数。

图 5 不同迭代次数的LDPC码性能曲线

[1] Shannon C E.A Mathematical Theory of Communication[J].Bell System Tech J,1950,29:147-160.

[2] R udiger Urbanke.Modern Coding Thoery[M].Cambridge:Cambridge University Press,2008.

[3] Berrou C,Glavieux A,Thitimajshima P.Near Shannon limit error—correcting coding and decoding:turbo-codes[C].In Proc of ICC,Geneva,1993,1064-1070.

[4] DJ CMackay.Good Error-Correcting Codes Based on Very Sparse Matrices[J].IEEETrans info Theory,1999,45(2):399-431.

[5] RG Gallager.Low-Density Parity-Check Codes[J].IRE Transactions on Information Theory,1962,8:21-28.

[6] Sae-Young Chung,G.David Forney,Thomas J.Richardson.On the Design of Low-Density Parity-Check Codes within 0.0045 dB of the Shannon Limit[J].IEEE Comm Letters,2001,5(2):58-60.

[7] Gallager R G.Low-Density Parity Check Codes[M].Cambridge,M A:MI T Press,1963.

[8] Xiao-Yu Hu,Evangelos Eleftheriou,Dieter-Michael Arnold.Regular and irregular progressive edge-growth Tanner graphs[C].Global Telecommunications Conference,2001:995-1001.

[9] Tanner R M,Sridharan D,etal.LDPC Block and Convolutional Codes Based on Circulant Matrices[J].IEEE Trans Inform Theory,2004,50(12):2966-2984.

[10] Fossorier M.Quasi-Cyclic Low-Density Parity-Check Codes From Circulant Permutation Matrices[J].IEEE Transactions on Information Theory,2004,50(8).

[11] CCSDS131.1-0-2.LOW density parity check codes for use in near–Earth and deep space application[S].CCSDS,2007.

[12] Richardson T,Urbanke R L.Efficient Encoding of Low-Density Parity-check Codes[J].IEEE Transactions on Information Thoery,2001,47(2):638-656.

[13] GYT220.1-2006,移动多媒体广播 第 1部分:广播信道帧结构、信道编码和调制,中华人民共和国广播电影电视行业标准[S].2006.

[14] 侯铭睿,史萍.非二进制 RS-Turbo级联码性能研究[J].中国传媒大学学报(自然科学版),2008,15(1):64– 68.