基于ARMA模型的振动信号建模与预测

曹昕燕,邹英永

(1.长春大学 电子信息工程学院,吉林 长春 130022;2.长春大学 机械工程学院,吉林 长春 130022)

基于ARMA模型的振动信号建模与预测

曹昕燕1,邹英永2

(1.长春大学 电子信息工程学院,吉林 长春 130022;2.长春大学 机械工程学院,吉林 长春 130022)

振动信号是反映系统故障的重要信息,预测振动信号的趋势是系统状态监测与故障诊断中的一个重要内容。本文提出了一种采用时间序列模型来分析和预测非线性随机振动信号的方法,建立了描述振动信号的数学模型。首先将现场测得的非平稳振动信号转化成标准正态平稳时间序列,然后利用这些参考信号建立时间序列模型,并采用非线性最小二乘法进行模型参数估计,最后利用该模型对信号进行预测。应用结果表明该模型能够很好地拟合振动信号时间序列,并取得了一定的预测精度,可以达到预测要求。

振动信号;时间序列;建模;预测;参数估计

0 引 言

机械系统的振动信号是反映系统故障的重要信息,在对机械系统进行状态监测与故障诊断过程中,及时检测机械系统振动信号动力学突变对机械系统早期故障的发现有着极其重要的作用。由于机械系统在工作过程中会产生撞击、速度突变、结构变形、摩擦变化等,常会引起非平稳、非线性振动,因此从机械系统中获得的振动信号也往往具有非线性、非平稳性特征,很难从观测数据直接分析系统的变化规律。本文提出了一种基于时间序列分析技术的振动信号处理方法,它是在振动信号监测的基础上,通过对动态参数进行建模与预测,来估计设备故障的传播和发展趋势,对设备的优劣趋势做出预测。该方法具有能反映系统的内在规律、预测精度高等特点,特别适合于对设备的各种未来信号进行预测,已被广泛地应用于机械故障诊断、交通运输等学科,并发挥着重要的作用。

本文应用时间序列分析的方法对机械系统的动态参数进行了识别,首先对机械系统进行测量,获得响应的时间序列,然后对时间序列建立ARMA模型,利用ARMA模型与系统动态参数的关系对振动信号进行监测和预测分析。

1 时间序列模型

时间序列分析的步骤包括数据采集与处理、模型识别、参数估计、预报与检验等[1]。时间序列建模的一般流程图如图1所示。

1.1 数据采集与处理

建立时间序列模型需要离散时间序列。设一个振动系统某测点的输出响应为离散时间序列{Xt}。对于离散时间序列{Xt},当其取值过大或过小时,为保证计算精度、减少误差、避免溢出,需要对离散时间序列{Xt}进行规一化处理。即当{Xt}满足均值为μ^,方差为δ^2的正态分布时,对{Xt}中各数据进行规一化处理

1.2 模型识别

模型识别就是根据动态数据处理阶段所获得的数据信息的先验知识来选择一种合适的模型。均值为零的平稳时间序列可以用自回归模型(AR)、滑动平均模型(MA)和自回归滑动平均模型(ARMA)三种模型来表示。其中ARMA模型是一种精确度较高的短期时间序列预测方法。他将预测对象随时间变化形成的序列,看作是一个随机序列,然后用相应的模型进行近似描述,再通过对相应数学模型的分析研究,能更本质的认识这些动态数据内在结构和复杂性,从而达到在最小方差意义下的最佳预测。

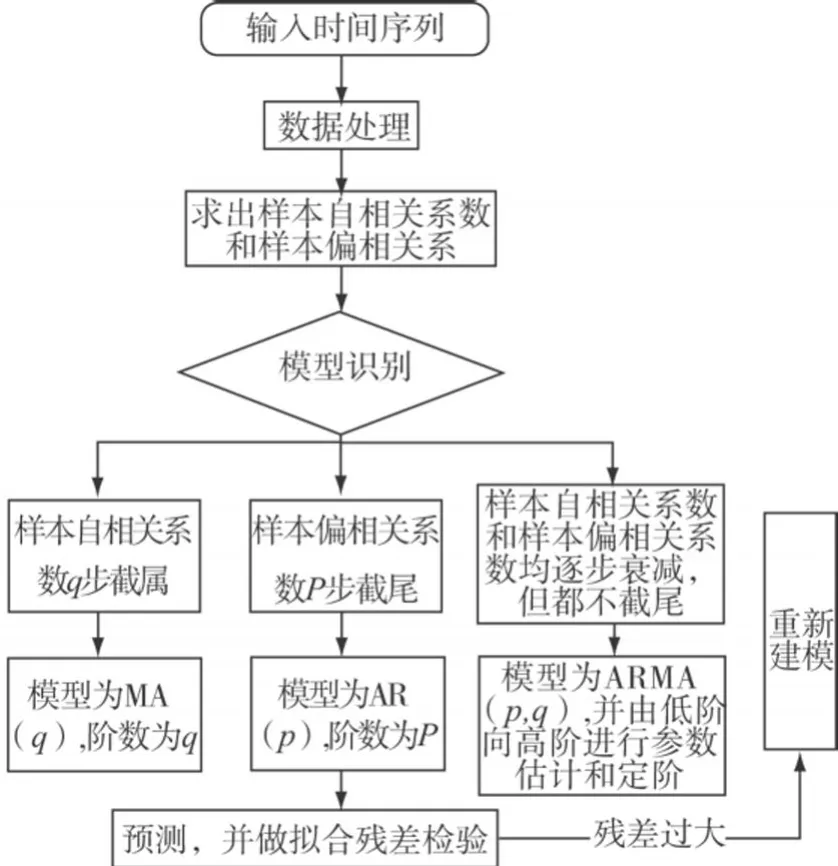
图1 时间序列建模过程

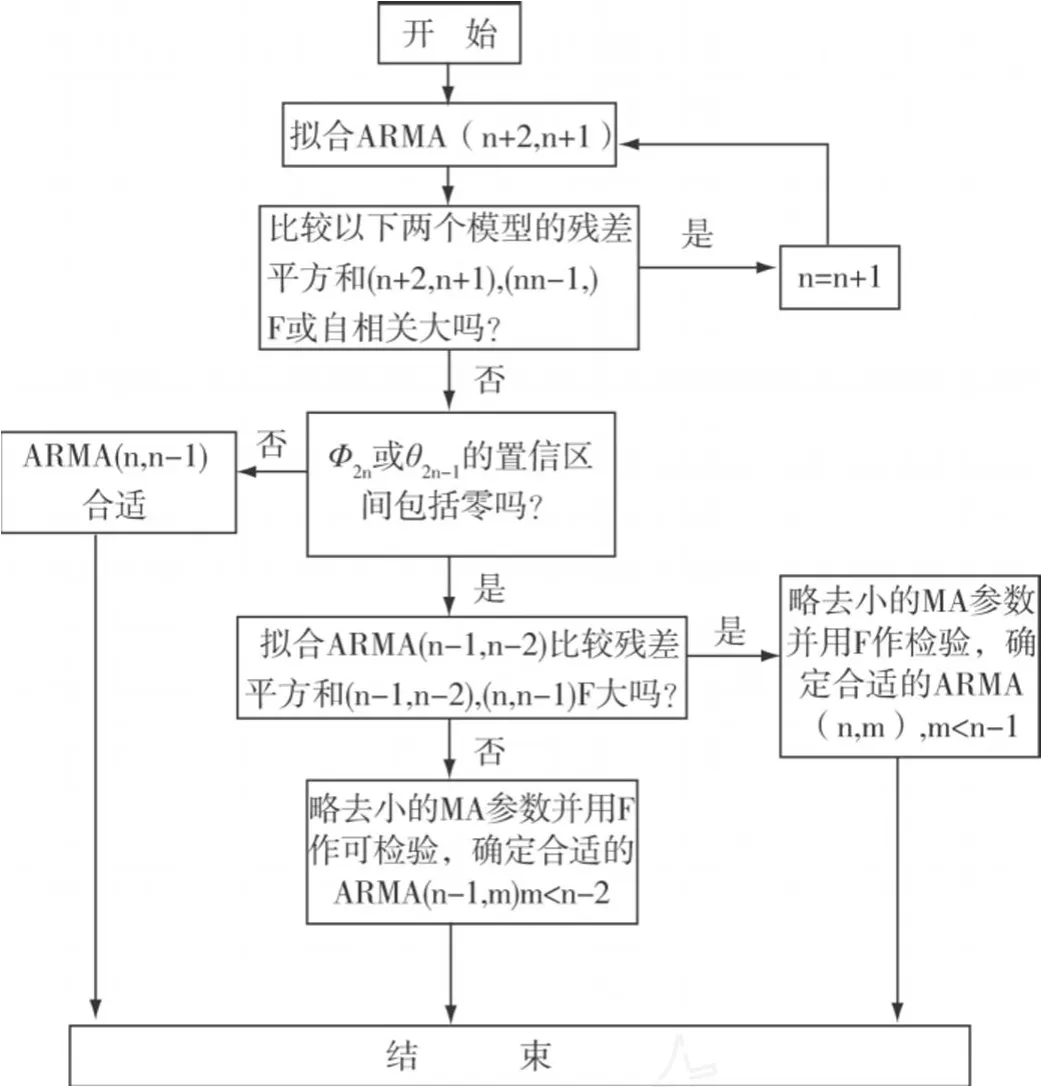
图2 ARMA模型建模流程

本文采用 ARMA(n,n-1)模型,其策略是用ARMA(n,n-1)模型的一个递增系列去逐步逼近数据的依赖关系。当用残差平方和的减小来作判断时,先停留在这样一个 n值上,即 n超过此值时,这种逼近的改善已不明显。应用这种策略可以设计一个简单的,能够在计算机上执行的建模程序,即只要把数据输入建模程序,就能输出所有的适合模型并指出最适合的一个模型,不需要对自相关、谱、残差等的图线进行实验验证。ARMA(n,n-1)模型的具体建模流程如图 2所示。

ARMA(n,n-1)模型的形式为[2]：

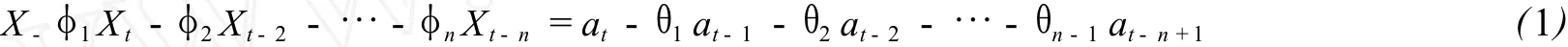
其中:at～N(0,σ)2

这种模型的形式是分别通过 n阶的自回归部分和 n-1阶的滑动平均部分去处 at对 Xt-1Xt-2,……, Xt-n和对 at-1,at-2,……,at-n+1的依赖关系。ARMA(n,n-1)模型的建模步骤为:

第 1步:拟合ARMA(n,n-1)模型,n值每次增加 1,利用 F判据检验残差平方和的改善情况,证实 at的自相关是在允许的范围内。在从ARMA(n,n-1)转到ARMA(n+2,n+1)时,当 F值在预定的水平上变得无意义时,就停止继续拟合,并选择ARMA(n,n-1)模型。

第 2步:检验 φ和θ,观察这些值与它们的绝对值相比是否小,他们的置信区间是否包括零,如果‘否’,则ARMA(n,n-1)为一个合适的模型。

第 3步:假如 F值小,并且它们的置信区间包括零,则拟合一个ARMA(n-1,n-2)模型,用 F判据检验它与ARMA(n,n-1)模型。假如 F值不大,则略去小的MA参数,拟合一个m＜n-1的ARMA(n-1,m)模型,并用 F判据检验,直至得到参数最少的合适模型为止。

第 4步:假如 F值大,则略去小的滑动平均参数,并确定m＜n-1的一个ARMA(n,m)模型。

第 5步:假如需要时,通过 F判据拟合模型的理想形式(如纯AR(n))或纯MA(m)等等),使模型的阶次逐渐增加,直至 F值小到无意义为止。

1.3 参数估计

模型的参数估计就是选择合适的参数使得模型的残差 at为白噪声。模型参数估计的方法很多,常用的方法有最小二乘估计、极大似然估计、最大熵估计和相关矩估计等方法。因为 ARMA(n,n-1)模型是非条件回归模型,所以它的参数采用非线性最小二乘法进行估计。

非线性最小二乘法采用逐步逼近的方法来实现 at的平方和的极小化。这个方法是从诸参数的某些初始值开始,利用公式(2)递推计算 at并求得平方和,然后通过最速下降法找到平方和减小的方向,再利用具有最小平方和的参数新值作为初始值,计算程序一直继续进行下去直至获得极小的平方和为止。

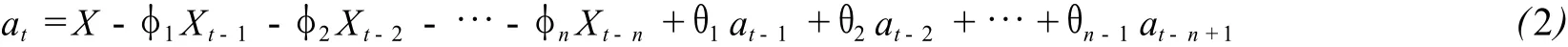
由于 t＜0时,不存在 Xt,所以将计算的第一个 at是在 t=n+1时刻的。对 t＜n的诸 at的初始值设其为零,则可以利用公式(2)递推生成 t=n+1,n+2,…,N时的各 at。可能会有少许的信息丢失,但当观测次数N较大时,则可忽略不计。

1.4 预测

预测是指已经知道一个时间序列现在与过去的数值,对将来的数值进行估计。时间序列预测的基本思想是根据当前及以前的观察数据对未来值进行估计。预测通常都采用最小方差线性估计的原则。首先将信号随机序列代入模型进行计算获得随机预测结果,然后根据在预测计算程序中所得趋势、周期、零均值计算等结果对预测结果进行数据还原即得实际预测数据。接下来读入下一步实测数据 Xt+1,保留最近的N个数据,然后进行趋势性周期性判别,进入下一次循环预测,从而实现对信号的预测。

1.5 检验

在建立了相关模型之后,为了判断该模型的优劣程度,需要对模型的拟合残差进行相关的检验分析。最简单有效的方法就是检验其拟合残差是不是白噪声。也就是说,如果经检验确是白噪声序列,则可认为模型是合理的,否则,就应当进一步改进模型。

2 振动信号的建模和预测

建模选择的信号源为振动信号,这些数据信号分为两部分,一部分用来建模,另一部分用来验证。原始信号分布如图3所示。

首先对初始数据减去平均值做为处理数据,然后依照上述分析建模方法,找出其合适的模型 ARMA(n,n-1),即确定正确的模型类别和模型阶次,然后利用建好的模型,预测出后面振动信号的值,再使用实际的振动信号值来检验预测信号的准确性。

利用上述数据,分别建立了ARMA(2,1),ARMA(3,2),ARMA(4,3),ARMA(5,4),ARMA(6,5),ARMA(7,6)6个模型,并用上述方法进行模型检验,结果如表 1所示。

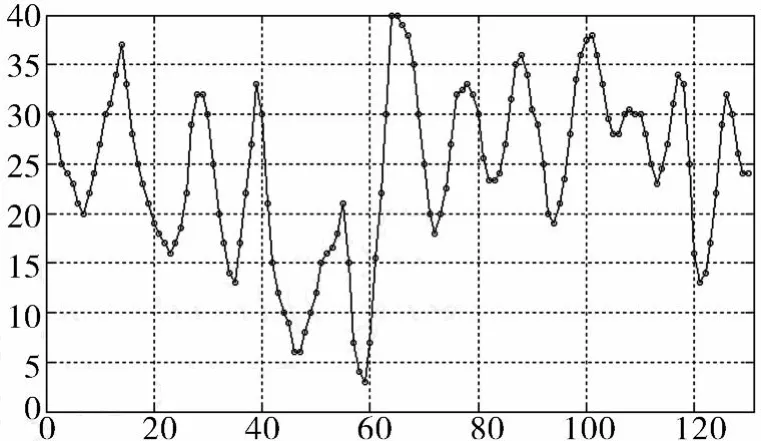
图 3 阻尼器机械振动系统响应数据分布曲线

表1 ARMA(n,n-1)建模参数表

图 4为不同模型残差图,通过对振动系统响应数据的残差平方和的比较,置信区间的选定,以及模型的适用性检验(F-检验法),可以确定出合适的时间序列模型为ARMA(6,5)模型。图 5为样本数据与不同模型预测值。

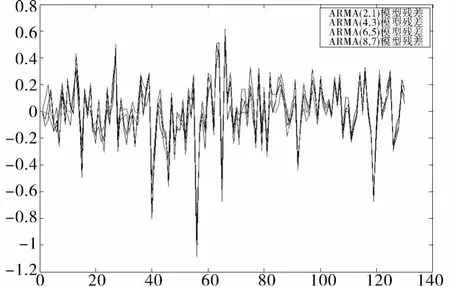
图4 不同模型残差图

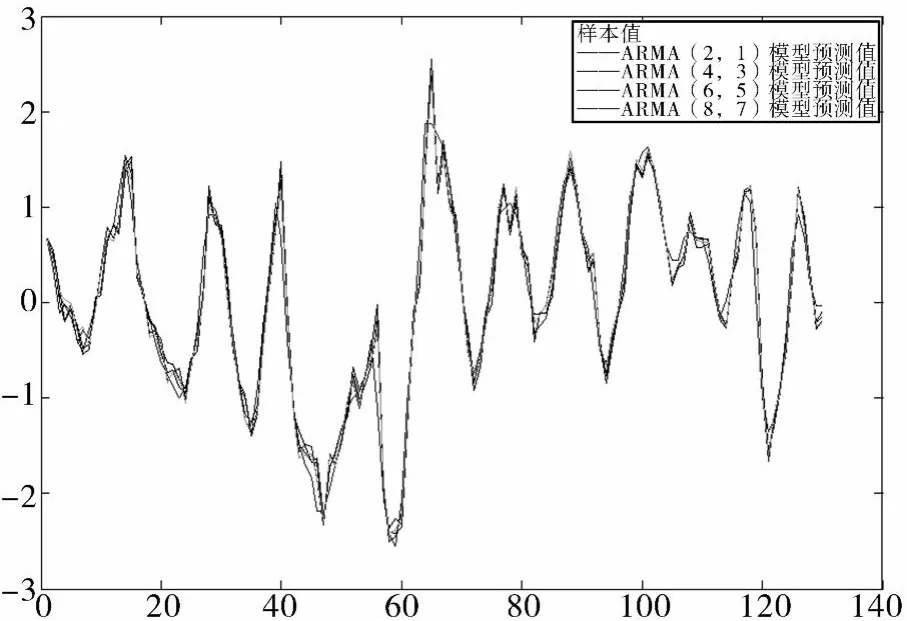
图5 样本数据与不同模型预测值

3 结 论

本文详细地论述了时间序列分析的原理和建模步骤,并给出了振动信号的预测过程和结果。从预测的结果可以看出,时间序列分析能够有效地识别机械系统的动态特性,且建模简单有效,具有较高的精度。该技术可以直接应用于设备的故障诊断中,利用现有的故障状态,预测出未来的故障趋势,做到提前防范、提前检修,具有极大的实际意义。

[1] 刘辉,潘迪夫,李燕飞.基于时间序列分析的机车振动信号建模和预测[J].铁道机车车辆,2007(8)：34-37.

[2] S.M.潘迪特,吴宪民著.时间序列及系统分析与应用[M].北京：机械工业出版社,1998.

[3] 韩路跃,杜行检.基于MATLAB的时间序列建模与预测[J].计算机仿真,2005,22(4)：501-701.

[4] 徐峰,王志芳,王宝圣.AR模型应用于振动信号趋势预测的研究[J].清华大学学报(自然科学版),1999(4)：57-59.

[5] 黄建洪,陈致伟,傅戈雁.时间序列预测模型的建模方法与应用[J].机械制造,2007(11)：1-3.

责任编辑：吴旭云

M odeling and forecast ing of vibration signals based on ARMA M odel

CAO Xin-Yan1,ZOU Ying-yong2
(1.College of Electronic Information Engineering,Changchun University,Changchun 130022,China; 2.Mechanical Engineering College,Changchun University,Changchun 130022,China)

Vibration signals are the important information for system failures.Forecasting the trend of vibration signals is an important contentof conditionmonitoring and fault diagnosis.This article presents amethod to analyze and predict nonlinear random vibration signals by t ime seriesmodel and establishesmathematicalmodels to describe vibration signals.Firstly,the non-stationary vibration signals acquired in the field are transfor med to stationary time series.Secondly,the time seriesmodels are constructed from the selected reference signals and nonlinear least square method is used to estimate models’parameters.Finally,the vibration signals are forecast by using the models.The application results show that the models can simulate t ime series of vibration signals quite wellwith good prediction accuracy and meet the need of forecasting.

vibration signal;time series;model;forecast;parameter est imation

TB53

A

1009-3907(2010)06-0052-04

2010-04-07

吉林省教育厅“十一五”科学技术研究项目[2009239]

曹昕燕(1973-),女,吉林长春人,副教授,博士研究生,主要从事信号处理方面研究。