考虑饱和-非饱和渗流作用的重庆奉节鹤峰乡场镇滑坡稳定性分析

李俊业，唐红梅，陈洪凯，曾 蓉

(重庆交通大学岩土工程研究所，重庆 400074)

考虑饱和-非饱和渗流作用的重庆奉节鹤峰乡场镇滑坡稳定性分析

李俊业，唐红梅，陈洪凯，曾 蓉

(重庆交通大学岩土工程研究所，重庆 400074)

岩土体中由于孔隙水压力的存在使得力学性状的分析变得更加复杂化，对饱和-非饱和渗流场的研究一直是岩土工程界的一大难点问题。基于三峡水库的库水位调度方案与实测月的降雨资料，分三种工况以极限平衡原理和Morgenstern-Price条分法为基础对重庆奉节鹤峰乡场镇滑坡进行了瞬态稳定性分析，研究了水分在坡体内的运移对边坡稳定性的时间影响效应。研究表明:场镇滑坡在库水位为145m与降雨耦合情况下，稳定系数1.15，不会失稳产生滑动;在降雨与库区水位175m和175m陡降至145m等因素耦合情况下失稳，稳定系数介于0.94～1.10，处于极限平衡状态及不稳定状态。

工程地质;饱和-非饱和渗流;稳定性分析;耦合;滑坡;三峡库区;重庆市奉节

0 引言

降雨是诱发滑坡的主要因素之一，目前，国外研究降雨入渗条件下的饱和-非饱和渗流场以及滑坡稳定性的成果很多。Nurly Gofar等［1］对降雨情况下的坝坡内的渗流场及坝坡稳定性进行了计算分析。DANG Thuong Huyen等［2］运用饱和-非饱和地下水流模型对地下水的渗流情况进行了数值模拟。Kassim等［3］对非饱和土层柱状渗流场进行了的数值模拟。我国学者也有大量的关于对降雨入渗影响边坡性状的研究。吴长富［4］、尹小涛［5］、林鸿州［6］等对降雨条件下边坡稳定性变化进行了分析。廖红建［7］、牛文杰［8］等对不同水位下的坝坡稳定性变化规律进行了分析。赵明华等［9］分析了降雨对路基的浸润作用，初步推导建立降雨作用下非饱和土路基的饱和-非饱和渗流公式。朱丽娟等［10］对降雨条件下非饱和黄土边坡含水量变化规律进行了研究。研究雨水入渗引发滑坡的物理过程并建立定量分析模型是降雨与滑坡关系研究的重要方面，探求降雨条件下边坡的瞬时渗流场是目前研究的难点所在。目前，对于降雨与库水位耦合因素影响下的地下水非稳定渗流分析方法尚待研究。

本文以重庆奉节鹤峰乡场镇滑坡为例，基于Fredlund提出的非饱和土抗剪强度理论，根据气象观测降雨资料和三峡水库的库水位调度方案的耦合情况，以极限平衡原理和Morgenstern-Price条分法为基础对鹤峰乡场镇滑坡进行了瞬态稳定性分析，分析了孔隙水压力场的变化及基质吸力在滑坡中所起的作用，为库区滑坡的监测、预报以及防治提供一定参考。

1 滑坡饱和-非饱和渗流模型

1.1 饱和-非饱和渗流控制方程

当地下水位埋藏较浅时，非饱和区土壤水的运动和饱和区水的运动是相互联系的，将两者统一起来即所谓饱和与非饱和问题。采用水头h作为控制方程的因变量，对于各向异性的二维饱和—非饱和渗流控制方程［11］为(假设土骨架不变形、水体不可压缩):

式中:kx、ky——x及y方向的饱和渗透系数;

t——时间;

ρw——水的密度;

g——重力加速度;

边界条件:

水头边界

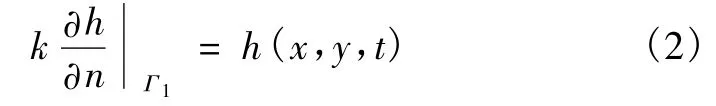
流量边界

式中:k——渗透系数张量;

n——边界面单位法向矢量。

2 计算模型

2.1 地质模型和初始条件

场镇滑坡位于长江南岸奉节县新迁鹤峰乡，距离奉节县老城约35km，属中低山之构造侵蚀—剥蚀深丘河谷地貌区，位于奉节县长江南岸支流墨溪河与九盘河交汇处上游的三角形地带，于墨溪河右岸斜坡下部，该段斜坡坡向北稍偏西，呈多级台阶状，由山顶至河底，斜坡地势呈缓→陡→缓→陡(滑坡后部)→缓(滑坡中部平台)→陡(滑坡前缘墨溪河)，平台地面坡度角一般 5°～10°，斜坡总体坡度角 20°～35°，地面高程140～400m，相对高差约260m。滑坡区两侧均被冲沟切割，中部高程约210m，地形较缓，坡度角小于10°，上下部地形较陡、坡度角 25°～35°。根据地质勘测资料，图1为场镇滑坡2-2’地质剖面。其各结构部位的物理力学计算参数选取见表1。

图1 场镇滑坡地质剖面Fig.1 Geologic section of changzhen landslide

滑体主要由粉质粘土、块石土及滑动岩体组成，表层局部分布人工填土，厚度变化极大。块石含量50% ～80%，粒径一般0.2～0.5cm，其间充填的粉质粘土呈可塑-硬塑，透水性好。厚度3.52～25.76m。

2.2 降雨边界条件及计算方法

场镇滑坡属亚热带季风性湿润气候区，为了全面分析该滑坡的稳定特性，在搜集奉节气象站1957～1988年共32 a的降雨观测资料［12］的基础上，特选定1982年7月(15 d)日降雨量作为降雨条件下该滑坡的渗流边界条件，降雨量历时曲线见图2。

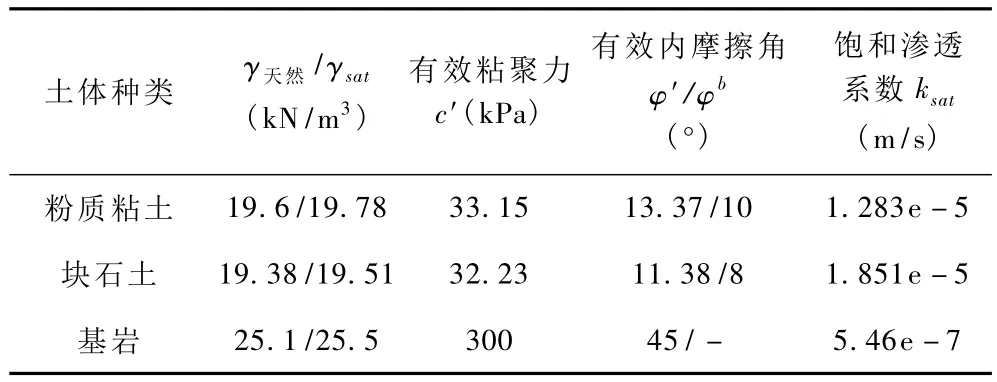
表1 岩土计算参数表Table 1 Calculation parameters

图2 奉节气象站1982年7月下旬降雨资料Fig.2 Rainfall data of weather station in Fengjie in late July 1982

由于勘察时仅测定了各土层的饱和渗透系数，计算所用土-水特征曲线是根据滑体和滑带饱和渗透系数大小和现场取土样后室内测得的土的粒径级配曲线分布规律由 Van-Genuchten模型拟合［11］推求其得到的。非饱和土土-水曲线如图3所示:

计算中采用地下水位为初始边界，对地面降雨的模拟采用在地表处设置单位流量边界，渗流计算时间步长为60s，共21600步。关于基质吸力对抗剪强度的影响文献［13、14］已经做过了详细的研究，本文采用Fredlund提出的考虑了负孔隙水压力的非饱和土抗剪强度理论:

式中:ua、uw——空气压力和孔隙水压力，本文中认为孔隙气压力等于大气压力;

c′、φ′——材料有效粘聚力和有效内摩擦角;

φb——抗剪强度随基质吸力增加的速率，为基质吸力的函数，文中假设φb为定值。

笔者在考虑负孔隙水压力对滑坡坡稳定性的影响时，采用了“总粘聚力”法［11］，在“总粘聚力”法中土的粘聚力 c值随着基质吸力的增大而增大，公式(4)变为如下形式:

公式通过变形以后与饱和土的抗剪强度公式保持一致，基质吸力产生的抗剪强度包括在土的粘聚力中。本文的计算中采用Morgenstern-Price法对库水位与极端降雨耦合情况下的稳定性进行评价。在稳定性计算中将土体的粘聚力c的一项由上式修正，使之更加符合实际。

2.3 计算工况

对于三峡库区的滑坡，最不利的因素是库水位骤降和降雨同时作用［15］。这里采用三种计算方案:

①工况Ⅰ，库水位145m+降雨作用;②工况Ⅱ，库水位175m+降雨作用;③工况Ⅲ，库水位降落+降雨作用，库水位降速为1m/d。

3 结果分析

3.1 饱和-非饱和渗流分析

本文采用Geostudio软件中的SEEP/W模块对库水位和降雨耦合情况下产生的渗流场进行数值模拟，模拟表明，降雨初期，降雨只作用到滑体前部，因此，地下水位没有变化，但浅层基质吸力明显减小且表层局部出现暂态饱水区;随着降雨量与降雨持时的增加，雨水不断向深部入渗，滑体基质吸力进一步减小，上部暂态饱和区逐渐扩大，雨水继续下渗并向坡脚汇聚，因此该部位饱和区域最先出现，并逐步向上推移;最后随着降雨持时增加，坡脚处的饱和区开始与地下水位相互连通，地下水位有所上升。工况Ⅰ天然状态和15d后、工况Ⅱ和Ⅲ下天然状态和2.5d后，斜坡内的孔隙水压力场，如图4、5、6所示:

工况Ⅰ时，地下水位以上基质吸力(负孔隙水压力)最大值为 40kPa，滑带土基质吸力最大值为30kPa左右，主要集中在滑带土中上部。随着降雨的持时增加，地下水位以上的最大基质吸力逐渐由40kPa减少到10kPa，并且地表逐渐出现暂态的饱和区。工况Ⅱ时，滑带土基质吸力减小至8kPa左右。工况Ⅲ水位变化和强降雨耦合时，滑带土基质吸力减小至5kPa左右，且影响范围明显减小，底部滑带土基质吸力基本丧失，对于坡体稳定安全不利。

图3 非饱和土土-水曲线Fig.3 Soil-water characteristic curve of unsaturated soil

图4 工况Ⅰ时不同时间下斜坡体内孔隙水压力分布图Fig.4 Pressure field distribution of pore water in slope on conditionⅠin different time

3.2 坡体渗流特性变化与强度耦合分析

孔压变化会引起应力应变的变化，应变的发生也会影响孔压的改变。为了进一步得到滑坡发生的内在原因，笔者绘制了工况Ⅲ(2.5d后)由计算得到的滑动面上某一点的土的抗滑强度与该点的水平坐标间的关系见图7。

由图7可以看出，滑动面的位置不同而导致非饱和土的强度变化呈现非线性变化规律，在距离为50m以内的滑动面上，由于负孔隙水压力的存在使得抗滑强度维持在一个较高水平，在接近100m处，由于上覆土层较厚，所以摩擦力达到最大，抗滑强度仍然维持在一个较高水平，随着距离的增大，孔隙水压力逐渐变为正值，基质吸力提供的强度全部丧失，加之上层覆土的重量逐渐减小，摩擦力随之剧减，总抗滑强度也随之减小为0。

3.3 坡体瞬态稳定性分析

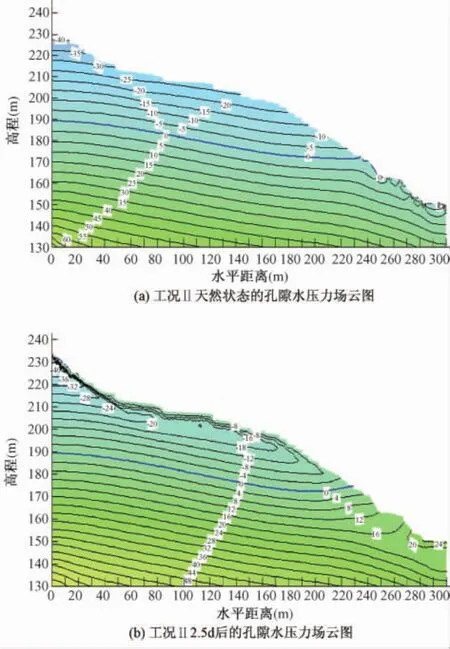
图5 工况Ⅱ时不同时间下斜坡体内孔隙水压力分布图Fig.5 Pressure field distribution of pore water in slope on conditionⅡin different time

为了解各个工况下降雨对边坡的影响时间和大小，在设计的工况下，利用 Geostudio中由 Seep/w中的计算结果导入Slope/w中对其瞬态稳定性进行了计算，绘制成稳定系数随时间变化曲线，如图8所示:

总体上，在降雨作用下，三种工况下的稳定系数都是在不断降低，由图8的三种工况下的稳定系数变化图可以看出，在前期降雨达到0.5d时，稳定系数都有一定量的增加，这是由于非饱和土在初始含水量较低时，随着含水率的增加，粘聚力先增加然后减小。从图8(a)可以看出，库水位保持在145m时，在一定量的前期降雨量后，高强度降雨对边坡的稳定性影响很不利，由于降雨入渗需要一个过程，在暴雨来临之后各方案条件下边坡都是在约1.5 d的稳定系数第1次迅速降低。在工况Ⅰ下，第一次高强度的暴雨来临后，稳定系数迅速下降，由图8(a)可以看出，在降雨作用下，稳定系数总体呈下降趋势，第一次暴雨之后，稳定系数有一个骤降，随着时间的增加，雨水向深层运动，稳定系数逐渐降低，到第二次暴雨来临之后，稳定系数再一次出现骤降。

图6 工况Ⅲ时不同时间下斜坡体内孔隙水压力分布图Fig.6 Pressure field distribution of pore water in slope on conditionⅢin different time

图7 非饱和土强度与滑带位置关系图Fig.7 The relationship between Location of Slip zone and Strength of Unsaturated soil

图8 各种工况下稳定性系数随时间变化图Fig.8 Factor of safety under various conditions overtime

工况Ⅱ下，库水位保持在175m，由于地下水位较高，天然状态下稳定系数为1.031，第一次暴雨后稳定系数迅速降低到1以下。

工况Ⅲ下，库水位由175m以1m/d下降，初始状态下稳定系数为1.031，第一次暴雨后稳定系数迅速降低到1以下，与工况Ⅱ比较，工况Ⅲ的稳定系数下降更为迅速。表明库水位下降情况与降雨耦合的情况对稳定性影响最为不利。

3.4 坡体渗流特性变化分析

综合来看，工况Ⅰ降雨使滑坡稳定系数由1.204下降至1.169，滑坡属于稳定状态，工况Ⅱ与工况Ⅲ下，均在第3天时，滑坡失稳。另外由图8可知，库水位对滑坡的稳定系数影响较降雨作用更直接。滑面的各个位置的负孔隙水压力如图9所示，

图9 各工况下滑面压力水头历时曲线Fig.9 Curve of pressure head duration on every condition

由于降雨强度小于上滑带的饱和渗透系数，坡顶处的直至滑坡发生都未能达到饱和状态，但是根据图9可知，滑坡表面在降雨的极短时间内，负孔隙水压力急剧减小，基质吸力接近为零，随着降雨持时的增加，滑坡表面的负孔隙水压力在-5kPa左右小幅度变化，降雨对滑面中部的负孔隙水压力影响较小;工况Ⅰ下，坡脚处的负孔隙水压力在0左右小幅变化，在工况Ⅱ和工况Ⅲ下，坡脚处的负孔隙水压力受到库水位的影响很大。工况Ⅱ时，坡脚处的孔隙水压力达到20kPa。工况Ⅲ时坡脚处的孔隙水压力由23kPa逐渐减小到0。由滑面压力水头变化情况可知，土中基质吸力的丧失是非饱和土坡发生滑坡的主要原因，坡脚处的孔隙水压力变化对滑坡的稳定性影响较大。

4 结论

库水位下降和降雨是导致滑坡的两个重要因素。本文通过实测降雨和库水位耦合情况下的暂态饱和与非饱滑坡渗流的有限元分析，结合实例计算，得到如下结论:

(1)库水位下降和降雨是导致滑坡的两个重要因素，在滑坡地下水位较浅时，降雨入渗容易使滑坡地下水位上升，引起非饱和土中基质吸力的丧失是导致土坡稳定性急剧降低的主要原因。鹤峰乡场镇滑坡在库水位为145m与降雨耦合情况下，稳定系数1.15，不会失稳产生滑动;在降雨与库区水位175m和175m陡降至145m等因素耦合情况下，滑动面抗剪强度降低，抗滑力减小，下滑力增大，稳定系数一般小于1.10、在0.94～1.10，处于极限平衡状态及不稳定状态。本文撰写时，勘察报告已对鹤峰乡场镇滑坡稳定性进行了计算，本文计算结果与鹤峰乡场镇滑坡稳定性结果相一致，证明本文计算方法具有可靠性。

(2)雨水入渗需要一个过程，所以边坡的稳定系数随着降雨历时的衰减有一个滞后。稳定系数均是在暴雨来临后的1.5d后出现骤降，这一点结论与实际情况相符合。

(3)基于饱和-非饱和渗流数学模型，运用延伸的摩尔库伦强度理论，对鹤峰乡场镇滑坡进行了极端降雨与库水位耦合情况下的饱和-非饱和渗流场计算和稳定性分析。本文采用实测的降雨资料与三峡水库库水位调度方案相耦合，使计算更加接近实际情况，具有一定的实用价值。

［1］Nurly Gofar，LeeMin Lee1，Marwan Asof.Transient seepage and slope stability analysis for rainfall-induced landslide:acase study［J］.Malaysian Journal of Civil Engineering，2006，18(1):1-13.

［2］DANG Thuong Huyen，KenjiJINNO and Atsushi TSUTSUMI.Assignment of the Groundwater Level at the Leachate Collection Pipe for the Waste Landfill Groundwater Simulation: Combination of the Two Dimensional Saturated-Unsaturated Vertical and Horizontal Groundwater Flow Model［J］，Memoirs of the Faculty of Engineering，2009，69(3):79-93.

［3］Kassim，Azman and Gofar，Nurly，et al.Min Lee.Numerical simulation of infiltration through unsaturated layered soilcolumn［J］.Malaysian JournalofCivil Engineering，2008，20(2):211-222.

［4］吴长富，朱向荣，尹小涛，等.强降雨条件下土质边坡瞬态稳定性分析［J］.岩土力学，2008，29(2):386-391.

［5］尹小涛，冉昌国，王水林.降雨条件下滴水崖Ⅰ号滑坡瞬态稳定性分析［J］.岩土力学，2008，29(2):501-506.

［6］林鸿州，于玉贞，李广信，等.降雨特性对土质边坡失稳的影响［J］.岩石力学与工程学报，2009，28(1):198-204.

［7］廖红建，姬建，曾静.考虑饱和-非饱和渗流作用的土质边坡稳定性分析［J］.岩土力学，2008，29(12):3229-3234.

［8］牛文杰，叶为民，刘绍刚，等.考虑饱和-非饱和渗流的土坡极限分析［J］.岩土力学，2009，30(8):2477-2482.

［9］赵明华，刘小平，何伟，等.非饱和土路基降雨渗流分析［J］.公路交通科技，2009，26(3):49-53.

［10］朱丽娟，王铁行，胡炘.降雨对非饱和黄土边坡含水量变化规律分析［J］.地下空间与工程学报，2009，5(1):95-99.

［11］Fredlund D.G，H.Rahardjo.非饱和土力学［M］.陈仲颐等译.北京:中国建筑工业出版社，1997.

［12］李晓，张年学，廖秋林，等.库水位涨落与降雨联合作用下滑坡地下水动力场分析［J］.岩石力学与工程学报，2004，23(21):3714-3720.

［13］朱青青，苗强强.非饱和土基质吸力对抗剪强度参数影响的探讨［J］.甘肃科学学报，2009，21(3):139-141.

［14］Ning Lu，M.ASCE，and D.V.Griffiths，et al.Profiles of steady-state suction stressin unsaturated soils［J］.Journal of Geotechnical and Geoenvironmental Engineering，2004，130(10):1063-1076.

［15］苏爱军.湖北省三峡库区滑坡防治地质勘察与治理工程技术规定［M］.北京:中国地质出版社，2003.

Stability analysis of Changzhen landslide in considering saturated and unsaturated seepage effects

LI Jun-ye，TANG Hong-mei，CHEN Hong-kai，ZENG Rong
(Institute of Geotechnical Engineering，Chongqing Jiaotong University，Chongqing 400074，China)

As the existence of pore water pressure in the rocks and soils，the analysis of the Mechanical properties of the matericals.becomes more complicated，Studying of saturated-unsaturated seepage has been a big and difficult problems in geotechnical engineering.Based on the water level scheduling scheme and the rainfall measured data in the Three Gorges Reservoir＇s，Using the limit equilibrium theory and Morgenstern-Price slice method Analyzed transient stability of HeFeng landslide Xiangchang Fengjie of Changqing in the three conditions，Researched time effects of slope stability of water moving in the slope body.The results show that:In the condition of the coupling of the 145m reservoir water level and rainfall，the stability coefficient of of Changzhen landslide in is 1.15，and will not loose stability or slide;Under the coupling of the 175m reservoir water level and steep dropping from 175m to 145m，the stability coefficient Ranged between 0.94～1.10，the landslide was in the limit equilibrium and unstable condition.

engineering geology;saturated-unsaturated seepage;stability analysis;coupling;landslide;Three Gorges Reservoir Area;Fengjie of Chongqing City

1003-8035(2010)04-0001-07

P642.22

A

2010-05-26;

2010-07-19

重庆市重点自然科学基金项目(2008BA0015);中国博士后科学基金特别资助项目(200902288);全国高校博士点基金(20080430095)

李俊业(1985-)，男，内蒙古巴彦淖尔市人，硕士研究生，从事岩土工程及水工结构研究。

E-mail:lijunye_2008@yeah.net