求最大完全子图的启发式着色算法
李建新
(1.宿州学院计算机科学与技术系,人工智能与数据挖掘研究室,安徽宿州234000; 2.合肥工业大学计算机与信息学院,安徽合肥230009)
求最大完全子图的启发式着色算法
李建新1,2
(1.宿州学院计算机科学与技术系,人工智能与数据挖掘研究室,安徽宿州234000; 2.合肥工业大学计算机与信息学院,安徽合肥230009)
本文提出了一种求最大完全子图的启发式着色算法.该算法通过为顶点着色将已知无向图划分为极大完全子图的并集,再根据各极大完全子图中顶点的多少选取最大完全子图.随后为提高算法执行效率,又对该算法提出了一种精简措施.最后将该算法运用于一集成电路测试数据编码压缩实验中,证明了该算法对求解最大完全子图的有效性.
最大完全子图;极大完全子图;启发式算法;着色算法
0 引言
最大完全子图(maximum comp leted sub-graph)问题是图论中的一个经典组合优化问题,也是一类NP完全问题,对它的研究具有很大的理论和实用价值,该问题在实践中被广泛应用于市场分析、方案选择、管理决策、故障诊断、数据压缩等不同领域.目前国内外对最大完全子图问题的求解有广泛的研究,大致可分为确定性算法(exact algorithm)[1]和启发式(heuristic algo rithm)[2-6]算法两大类.确定性算法在求解顶点数相对较少、密度相对较低的图时尚为有效,随着研究的深入,遇到的问题复杂度越来越高(顶点增多和边密度变大),确定性算法逐渐不能有效解决.针对该情况,一些学者提出了启发式算法求解最大完全子图问题,当前的启发式算法都基于以下几类:顺序贪婪启发式算法[2]、遗传算法[3]、神经网络[4]、模拟退火和禁忌搜索[5]、基于连续的启发式算法[6]等,取得了令人满意的效果.
着色算法是图论中的一种经典算法,它通过对图的顶点着色或边着色的途径在方案选择及地图学等各个领域有着广泛的运用.但通过文献查询,目前还没有发现运用着色手段求解最大完全子图的成熟算法,经研究,本文推出一种对无环的简单无向连通图求解最大完全子图的着色算法,该算法也是一种启发式算法.
1 算法思想的由来
该算法思想来源于本人对集成电路的测试向量相容压缩的研究.在对集成电路进行测试时,需要通过自动测试设备A TE(automatic test equipment)向测试芯片传输大量的测试数据,为减少测试时间,降低测试成本,需要对测试数据进行压缩,由于测试数据中含有大量无关位,向量间的相容性较好,因此可对测试向量采取相容压缩的方法.相容是指两测试向量对应位相同或其中一位为无关位,相容压缩是将测试集中相容的测试向量合并为一个向量.为追求最大压缩率,需寻求测试集中的极大相容类,这个问题可映射为图论中的极大完全子图问题,并且可通过为顶点着色分类的方法划分各个极大相容类,进一步研究可将该方法演化为求极大完全子图(great completed subgraph)的一般算法,进而也就得到了求最大完全子图的算法.
2 相关概念
定义1[7]通常把二元序组(V,E),称为图.记为:G( V,E),或G=(V,E).其中:V表示顶点集,V(G)={图G中顶点的集合};E表示边集,E(G)={图G中边的集合};
定义2[2]设H=(V’、E’),V’⊂V,E’⊂E.如果∀x、y∈V’,H中都有连接x与y的边,则称H是G的完全子图.如果不存在G的完全子图M,使得V(H)⊂V(M),E (H)⊂E(M),则称H为G的极大完全子图.|V(H)|值最大的极大完全子图称为最大完全子图.
引理[8]设R是集合A上的关系,P1、P2……是A中的所有等价类,于是A=P1∪P2∪P3……且Pi∩Pj=Φ(i≠j)
结论1[8]极大完全子图的点集在两两相邻的关系下是一等价类.
结论2[8]任意图G的点集P(G)可划分为所有极大完全子图的并集,即P(G)=P(G1)∪P(G2)∪…∪P(Gk)∪…,且P(Gi)∩P(Gj)=φ,i≠j.Gi(i=1,2,…)是G的极大完全子图.
3 求最大完全子图的着色算法
3.1 算法描述
由上述结论2,任一无向图G均可以划分为极大完全子图的并集,因此可以对一无向图进行极大完全子图化.本算法首先按从大到小的顺序产生出各个极大完全子图,同时对不同的极大完全子图的顶点着不同的颜色,然后返回着某种颜色最多的极大完全子图即为最大完全子图.为更突出表现算法思想,本算法采用清晰的自然语言进行表达,描述如下:
根据实际问题进行抽象,建立一无向图G=(V,E);
for(对于每个顶点v)
{Full_degree=0;
Uncolor_degree=顶点v的度;}
按照一定的顺序放置颜色c1,c2,…,ck;初始化各颜色数值c1=c2=…=ck=0
w hile(G中所有顶点未完全着色)
{
v=Full_degree最高的未着色顶点,
Full_degree相同情况下是Uncolor_degree最高的未着色顶点,
两者都相同情况下是索引较小的未着色顶点;
j=某种颜色的索引,这种颜色若已出现过,则着该颜色的全部顶点都要落在v的已着色的邻接顶点范围内,若没有任何一种颜色的全部出现在v的已着色的邻接顶点中,则j为从未出现过的颜色的最小索引;
fo r(与v邻接的每个未着色顶点u)
{Full_degree++;
Uncolor_degree--;}
v的颜色=cj;
cj++
}
Return cj最大的完全子图
3.2 算法运用举例
为便于理解上述算法,现举例说明,建立一简单无向图如图1所示,对该图运用上述启发式算法进行着色的过程以及算法中关键变量的变化过程如表1所示,其中顶点序号vi是指图1中的各个顶点;si是第指第i步,即stepi,其中s0是指初始状态;指针指向第i步所考察的需着色的顶点,每一步考察一个顶点及其与邻接顶点的关系,并对它进行着色;Cj是颜色序号;Full_degree和Uncolo r_degree是控制各顶点着色情况的两个变量;“无”是指初始时各顶点均无颜色;“-”是指保持前边的值不变.
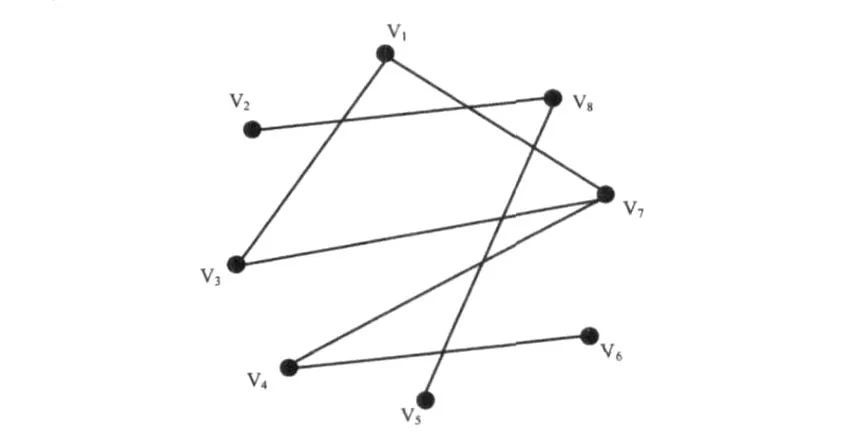
图1 已知无向图例图
最终实现极大完全子图的划分结果如下:
着C1颜色的顶点集V(G1)={v1、v3、v7}
着C2颜色的顶点集V(G2)={v4、v6}
着C3颜色的顶点集V(G3)={v2、v8}
着C4颜色的顶点集V(G4)={v5}
经比较知,由顶点集V(G1)构成的完全子图即为最大完全子图.
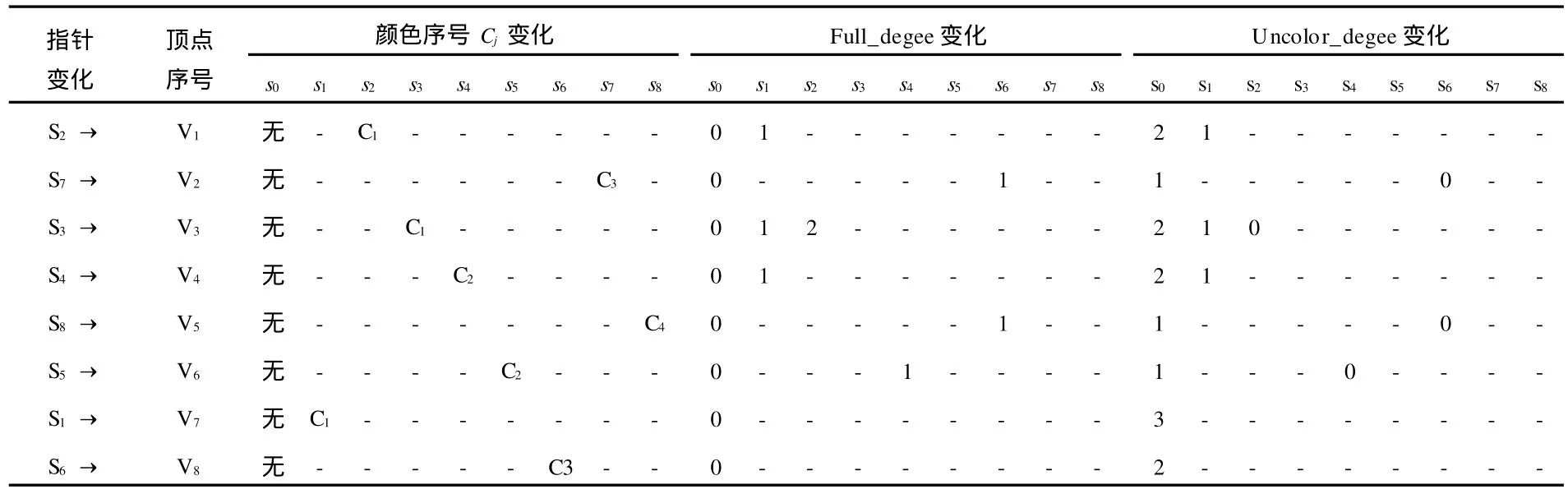
表1 顶点着色过程及算法中关键量的变化过程
3.3 算法运用的精简预处理
在实际问题中,经常会遇到不必求解出所有的极大完全子图,而只需要求出几个相对较大的完全子图的情况,在这种情况下,可以先对已知图进行适当的精简处理,再运用上述启发式算法求解,将会大大提高算法执行效率.经过大量实例研究表明,一个图的较大完全子图往往存在于度数较高的一定数量的顶点之间,因此,对复杂图精简处理时可采取适度删除低度数顶点及其边的措施来降低图的复杂性,进而降低算法执行的时间和空间复杂度.比如在上述图1中,如果先删除掉度数为1的顶点V2、V5、V6及其由它们发出的边,图1将变为如图2所示,这时再运用着色算法求解最大完全子图(由顶点V1、V3、V7组成),算法执行效率会更高.

图2 图1精简处理后的例图
4 实验验证
本算法在集成电路测试数据某相容压缩实验中得以运用,顺利地完成了实验任务,使实验达到了预期的结果,同时验证了本算法的有效性.实验中以ISCAS-89基准电路的几个规模较大的时序电路的M intest测试向量集的测试向量作为实验对象,整个实验在VC++环境中实现.为了提高向量间的相关性,对集成电路S5378f、S9234f、S13207f、S15850f、S38417f、S35854f的各个测试集均采取了分组相容的措施,首先将测试集按列分组,根据每组测试分量间的相关性建立相关性无向图(以邻接表存储),图的顶点表示测试分量字段,边表示测试分量间具有相关性,然后运用上述算法划分极大完全子图,每一个极大完全子图内的测试分量是两两相关的,可以合并为一个测试分量,达到压缩的目的.因此随着分组方法的不同,构建的相关性无向图边数是大不相同的,边数统计不具有确定性,但顶点数目是固定的,各测试集构成的无向图的顶点数规模如表2所列.
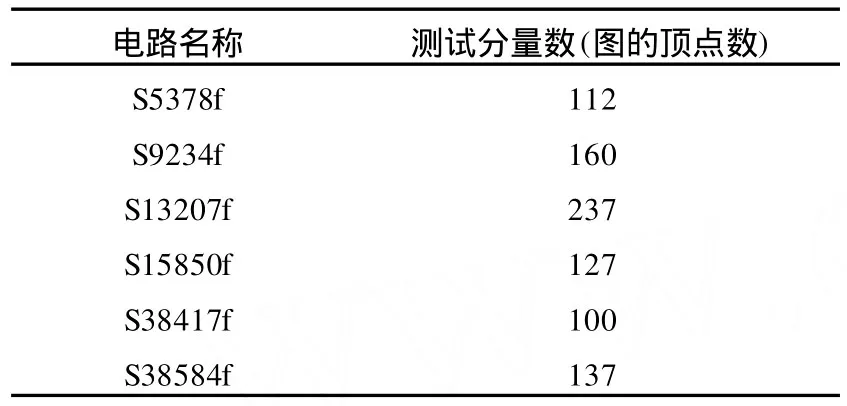
表2 实验用图顶点数
由表2可看出由各测试集的测试分量构成的图的顶点规模是较大的,由此也可以窥见图的复杂性,并且分组越多,测试分量间的相关性越好,图的边密度越大.本算法在此实验中发挥了巨大的作用,同时也显示了它在求解多顶点高密度图最大完全子图问题中的有效性.
5 结束语
本文从理论到实践阐释了一种用于求解最大完全子图的启发式着色算法,该算法思路清晰,通过实验证明该算法在处理多顶点高密度无向图时较为有效.但作为一种启发式算法,还有可能存在找不到最优解,而只有近优解的情况,因此本算法还有必要继续优化.实践证明,在上述算法演进一节中所述的降低图的复杂性的精简处理措施除了可提高算法的执行效率外,还有利于增加极大完全子图的确定性,遴选出最大完全子图,找到近优解.因此算法的优化除对算法本身进行改进外,还可考虑在不同需要的情况下对图采取适当的精简措施,另外,还可在图的存储结构等方面进行研究.
[1] ADLEMAN L M.Molecular computation of solutions to combinatorial p roblems[J].Science,1994,226(11):1021 -1024.
[2] 郭 平,康艳荣,史晓晨.基于最大code码的极大完全子图算法[J].计算机科学,2006,33(2):188-190.
[3] CARTER B,PARK K.How good are genetic algorithms at finding large cliques:an experimental study,Technical Report Bu-CS-93-015[R].Boston:Computer Science Dept.,Boston University,1993.
[4] BALLARD D H,GARDNER P C,SR IN IVASM A.Graph p roblemsand connectionist architectures,Technical Report TR 167[R].New Yo rk:Dep t Computer Science,University of Rochester,1987.
[5] AARTS E,KORST J.Simulated annealing and boltzmann machines,astochastic app roach to combinational op tim ization and neural computing[M].New York:Wiley,1989.
[6] PARDALOS PM,PH ILL IPSA T.Aglobal op timization app roach forsolving the maximum clique p roblem[J].International Jou rna l o f comp uter Mathema tic s,1990,33:209 -216.
[7] 孙 晶,张东林.离散数学[M].沈阳:东北大学出版社2004:103.
[8] 王世昌,兰绍玉.极大完全子图在管理决策中的应用[J].计算机应用,1995,15(4):29-31.
Heuristic Coloring Algorithm for a Maximum Complete Sub-graph
L IJianxin
(1.Department of Computer Science and Technology,Suzhou College,Suzhou 234000,China; 2.School of Computer and Info rmation,Hefei University of Tchnology,Hefei 230009,China)
A heuristic coloring algorithm for amaximum comp lete sub-graph wasput forward.According to the algorithm,a know n undirected graph wasmade into a union of great comp lete sub-graphs by coloring the vertices,and then amaximum comp lete sub-graph was selected according to the number of vertices in each great comp lete sub-graph.Subsequently,in order to imp rove the execution efficiency of the algo rithm,it w as simp lified.It w as finally put into use in an experiment of test data coding comp ression of an integrated circuit,w hich p roved that it w as effective in determ ining a maximum comp lete sub-graph.
maximum comp lete sub-graph;great comp lete sub-graph;heuristic algorithm;coloring algo rithm
book=1994,ebook=16
O157.6
A
1673-1794(2010)02-0009-03
李建新(1971-),男,实验师,在读硕士,研究方向:算法设计、SOC测试方法.
安徽省自然科学研究重点项目(KJ2010A 352),安徽省自然科学研究一般项目(KJ2010B224),宿州学院硕士科研启动基金项目(2009YSS12)
2009-11-07

