一种基于正交表的工程无混杂试验设计法

韩 冰，唐 硕

（西北工业大学 航天学院，西安 710072）

一种基于正交表的工程无混杂试验设计法

韩 冰，唐 硕

（西北工业大学 航天学院，西安 710072）

文章提出了一种灵巧的试验设计法，它能根据工程实际中因素间的交互作用，在正交表中选择恰当的列作为主因素列，使所有交互作用列与主因素列无混杂。此外，在设计过程中分别引入动态规划法和微分进化法对各主因素列进行了均匀性优化，并根据数值实验结果，得出两种方法的优化效果随因素数和因素水平数的变化规律。

正交设计；交互作用；均匀性；动态规划；微分进化

0 引言

近年来，试验设计理论在工程实际中得到了广泛应用。为评价设计表的统计推断能力，提出了许多优良性准则。其中，以正交性[1]为设计准则的正交设计与以均匀性[2]为准则的均匀设计都获得了成功。Ma等[3]进一步研究了正交性与均匀性的关系，为正交表的均匀性优化提供了理论依据。

目前，试验设计技术逐渐应用于飞行仿真中，如选择多种飞行器方案，分析干扰因素的影响，优化设计参数等。飞行仿真试验的因素多，因素水平高，因素间交互作用强。于是，设计的分辨力变得十分重要。Box和Hunter[4]对正规设计提出了最大分辨力准则，Ma等[5]进一步提出广义最小低阶混杂（GMA），将该准则推广到非正规设计情形。Fang等[6]描述了2水平设计的均匀性与混杂的解析关系。最近，Sun等[7]提出了基于GMA准则的一种析因设计。以上设计法均假设主因素间的交互作用未知，而在工程实际中，因素间存在的所有显著的交互作用往往是已知的。这就迫切的需要一种已知交互作用与主因素无混杂的设计，能够排除不存在的交互作用对试验表设计过程的干扰，从而保证在实际无混杂的同时最大限度地减小试验次数。在正规正交表的构造算法[8]的基础上，本文提出了一种灵巧的设计程序，能根据用户输入的交互因素表，自行选取相应正交表的恰当列作为主因素列，使设计表能分辨出所有的主因素效应与交互效应，并对主因素列进行均匀性优化。

1 交互作用列表设计法

交互作用列表设计法，是在正交表中选取主因素列并计算交互作用列的方法，它必须保证所有主因素列不与任一交互作用列混杂。

1.1 正交表的构造及交互列的定义

本文涉及的正交表均为Ln(Sm)型正规正交表。马希文[8]详细描述了它的构造方法，并给出了交互作用列的定义，均为本文采用。此种正交表构造法为：设域Z中的元素为0,1,…s-1，Zk为定义在域Z中的所有k维向量组成的线性空间。按字典顺序将Zk中的全体向量推成一个Sk×k的矩阵C，从C中抽取第一个非零元素为1的行，可得到矩阵P0,将P0的列的顺序颠倒过来，即得生成矩阵P。设计矩阵F=CPT。将矩阵F的每个元素加1，即得到Ln(Sm)型正规正交表。

生成矩阵P的行向量为F中对应列的生成向量。于是给出交互作用列的定义：设D1,D2是F中两个不同列，则D1,D2的生成向量形成的线性空间中，所包含的矩阵P中的其它行向量在F中的对应列叫做D1,D2的交互作用列。推广至n列情形：设 D1,D2,…,Dn是 F中 n个不同列，则 D1,D2,…,Dn的生成向量形成的线性空间中，所包含的P中的所有行向量在F中的对应列，除去所有比D1,D2,…,Dn低阶的交互列，得交互作用列。其中，低阶交互列包括：D1,D2,…,Dn中各因素两两组合的交互效应列（称2阶交互列），3阶交互列,…,n-1阶交互列。

1.2 交互作用的录入约定

为表述方便，本文将主因素分为两类：已经确定列号的主因素称为旧因素，待选列号的主因素称为新因素。可将所有交互作用编制成表(下文称录入表)，录入到计算程序中。录入表的一行称为一个录入行，它是一个需计算的交互作用，参与交互作用的所有主因素编号记录在该行的每一列上。计算程序按行依次读取，选择本行的新因素列并计算其交互作用列，同时进行必要的校核，这一过程称为一个计算循环。为方便计算，对交互表的因素排列顺序作如下约定：编号较小的因素的首次录入先于编号较大的因素；旧因素间的新交互作用，排在含新因素的交互作用前；同一行中旧因素在前，新因素在后。

例：若需计算因素 1×2,1×3,1×4,1×2×3,1×2×4,1×3×4 的交互效应，约定录入表格式形如表1：

1.3 选择新因素列的原则

新因素列的选择需要满足三个原则：

（1）新因素列不能为旧因素列；

（2）新因素列不能为任一交互列；

（3）新因素列不能为任一交互作用的任一低阶交互列。

明显的，违反了第1，2个原则，将发生混杂现象。而违反原则3的设计没有意义。事实上，我们考虑高阶交互作用的影响，是基于一切较之低阶交互作用都有显著影响的情形，或者说，在一般情况下，设计高阶交互作用列，必须先设计一切较之低阶的交互作用列。

1.4 新因素列的校核

设计表中所有未指定因素和交互作用的列称为赋闲列。赋闲列是满足原则的必要非充分条件。必要性是明显的，非充分性是因为在大多数情况下，并不需要考虑旧因素的所有组合的交互作用，这就使得赋闲列中存在这种 “潜在组合”形成的交互列（下文称潜在列）。若选取赋闲列中的潜在列作为新因素所在列，将会有违反原则的可能；而将其从可选列中一概除去，会造成很大的浪费，因为并不是所有潜在列均违反原则，而且，在某次计算循环中违反原则的潜在列，并不是在之后的所有计算循环中必定违反原则。校核的实质是将违反原则的潜在列从本次计算循环的可选列中除去，从而达到保留可行的潜在列的目的。潜在列违反原则的情形有两类，第一类情形是：在录入行带有新因素的计算循环中，选定新因素列后，计算所得的交互作用列与某旧因素列混杂。若录入行中同时含有新因素及某“潜在组合”中的旧因素，或同时含有两个新因素，均可引发这类情形。此时计算程序需重新选择赋闲列中的其余列并校核是否发生混杂。值得注意的是，计算程序一次只选定一个新因素列并校核。这就避免了一次校核两个新因素列的情况。第二类情形是：在录入行带有旧因素间的某个新组合的计算循环中，计算所得的交互列与某旧因素列混杂。潜在列违反原则的错误事实上发生在之前最后一次选取新因素列的计算循环中。此时计算程序应当退回至发生错误的计算循环，并重新选择其它赋闲列为主因素列。

1.5 交互作用列表设计算法与算例

完整的交互列表设计算法如下：

步骤1.初始化程序：主因素1、2所在列自动选为正交表的列 1、列 2。

步骤2.从录入表录入一行，本次计算循环开始。新因素备选列为所有赋闲列。

步骤3.读入全部旧因素，若旧因素数大于1，则计算它们的交互作用列并校核。若校核失败，程序转至记录的录入表录入状态处并从备选列中剔除记录的主因素号；校核成功则继续；

步骤4.读入新因素后记录当前录入表录入状态（即：录入表的行列号，新因素编号，旧因素编号，旧因素列号，旧交互作用列号）；

步骤5.将备选列中列号最小的选定为新因素列，并进行校核。校核成功则记录选定的主因素列号；校核失败则将此列剔出备选列并重新选择。若直至无备选列时仍校核失败，则中断程序，并要求增大正交表规模；

步骤6.若本行仍有新因素未录入，则继续读入一个新因素并转步骤4；否则进行下一步；

步骤7.本次计算循环结束。若录入表仍未读完，则转步骤-2；否则算法结束。

现在给出L81340型正规正交表的交互作用列表设计实例。取表1为录入表，将其输入程序后得各主因素列与交互列如表2所示。

依交互列的定义，可以很方便的检验计算结果的正确性。

图1给出了程序设计流程示意图。

2 设计的均匀性优化法

2.1 均匀性优化与均匀性准则

方开泰[9]对正规正交表进行了如下均匀性优化：将正规正交表的列的水平作置换，得到 (S！)m个同构的正交表，选取均匀性最好的表作为使用表。本文选取中心化L2-偏差（CD2）作为均匀性准则。对于大规模的飞行仿真试验，对同构正交表逐一搜索的方法计算量巨大，以至无法完成。本文主要采用动态规划法和微分进化算法对正交表进行优化。

2.2 融合交互作用列表设计的一体化优化方案

对正交表的均匀性优化，本质是对采样点在试验区域内的均匀性优化。或者说，是优化主因素所在列，而对交互作用列的优化没有任何意义。故需将交互作用列表设计与均匀性寻优相结合。

2.2.1 基于动态规划的一体化优化方案

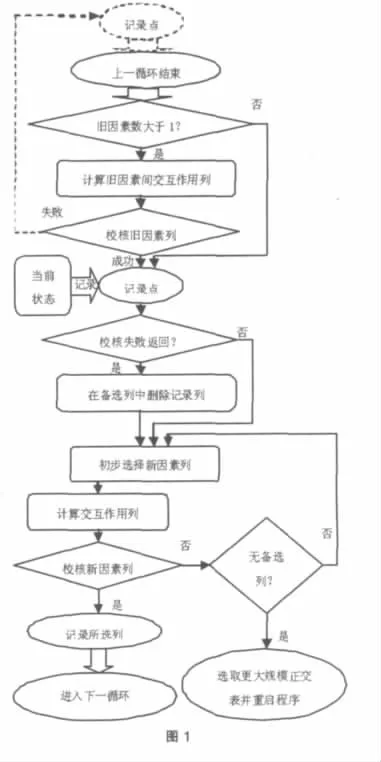
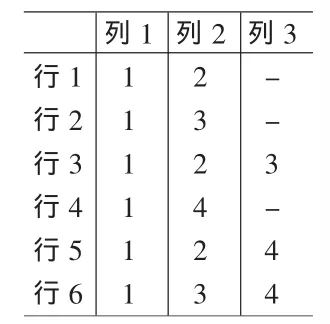
表1 一个录入表示例

表2 算例结果

表 3 L27313优化效果对照表

表 4 L81340优化效果对照表

表 5 L64421优化效果对照表

表 6 L125531优化效果对照表

本方案需对交互作用列表设计做以下改进：首先，原设计中因素1,2所在列默认为原正交表的1,2列。改进方案为，因素1所在列仍为原表第1列，而在其余n-1列中顺序取出每一列与第1列搭配，并对所选列作水平置换。选取使搭配的均匀性最佳的列的置换作为因素2所在列；其次，原设计中，当读入新因素时，选取列号最小的备选列作为新因素列。改进方案为，在备选列中顺序取出每一列与旧因素列搭配，并对所选列作水平置换。选取使搭配的均匀性最优的列的置换作为新因素所在列；最后，在设计结束后对赋闲列进行优化：在赋闲列中顺序取出每一列作水平置换，并与已选主因素列搭配，选取均匀性最好的，而后再在剩余赋闲列中按相同方法挑选出最优列，直至赋闲列全部优化完毕。

2.2.2 基于微分进化的一体化优化方案

本方案需对交互作用列表设计做以下改进：首先，在不考虑交互作用的情况下，对原正交表进行编码并优化。正交表的编码方案为：对表的每列的所有S!种水平的排列（即水平置换方案），按从小到大的顺序依次编码为0,1…,S!。排列的大小定义如下：一个排列的“值”对应于一个s位十进制数，它的第k位恰为在排列中位于第k个的数，排列的大小以该值的大小表征。依上述编码方式，m列的正交表可编码为一个m位S!进制数。本文选择最大进化代数为1000，种群规模为水平数的5倍，交叉因子为1，交叉概率为0.1，依微分进化算法[10]寻优。寻优结束后开始交互作用列表设计，当读入新因素时，令各备选列（不作水平置换）与旧因素列搭配，选取均匀性最优的备选列为新因素列。

2.3 优化效果对比实验

现在分别使用两种优化算法对L27313,L81340,L64421,L125531进行优化设计，要求考虑主因素1与2，1与3的交互作用。表5—8给出了不同主因素总数下的优化结果的均匀性以及程序耗时（本程序在AMD（主频2.01G）微机上运行，运行环境为32位Microsoft Windows操作系统）

通过对比以上实验结果，得出如下结论：首先，通过对照各表结果，可发现当主因素只有参与交互的三因素时，原设计表的均匀性偏差很小，此时优化效果微弱(CD2值在小数点后15位才有所降低)。当因素总数增多时，原表均匀性降低（这印证了设计的均匀性与分辨力的关系），而两种算法的优化效果逐渐增强。微分进化所得结果的均匀性更好，计算时间也更多。随着正交表水平与设计维数（生成矩阵P列数）的增加，微分进化与动态规划的耗时比先增加，后减少；其次，对比表3与表4，可发现当正交表水平数一定，而设计维数变大时，动态规划的效果有所下降，而微分进化几乎不受影响；而对比表3与表6，可发现当正交表设计维数不变，而水平数增大时，两种优化算法的效果均明显增强。表5为一个特例，此时动态规划所得某些结果的均匀性偏差稍稍高于原设计表，而微分进化所得结果则优于原表。这突出反映了基于动态规划法的优化方案无法收敛至全局最优，这是因为它在优化的每一个阶段，只保留了最优值，而失掉了有潜力的次优值。值得注意的是，在大多数情况下，动态规划法能快速稳定的优化原表，而微分进化优化结果有随机性。以上各表中“微分进化”的优化数据均为多次独立执行优化程序所得的最好结果。

3 结束语

数值实验的结论表明，本文提出的灵巧设计，能分辨出工程中的各主效应和交互效应。大样本强耦合的正交设计的均匀性快速全局寻优较为困难，本文给出的优化方案均实现了不同程度的优化。对程序代码段的测试表明，均匀性指标值的计算耗时随正交表规模的增大而显著增加，这是制约优化算法快速性的主要因素。

[1]田口玄一著，魏锡禄等译.实验设计法[M].北京：机械工业出版社，1987.

[2]方开泰.均匀设计与均匀设计表[M].北京：科学出版社，1994.

[3]C.X.Ma,K.T.Fang,Dennis K.J.Lin.A Note on Uniformity and Orthogonality[J].Journal of Statistical Planning and Inference,2003,（113）.

[4]G..E.P.Box,J.S.Hunter.The 2k-p Fractional Factorial Designs[J].Technometrics,1961,（3）.

[5]C.X.Ma,K.T.Fang.A Note on Generalized Aberration in Factorial Designs[J].Metrika,2001,（53）.

[6]K.T.Fang,R.Mukerjee.A Connection between Uniformity and Aberration in RegularFractions ofTwo-levelFactorials[J].Biometrika,2000,（87）.

[7]Fasheng Sun,Min-Qian Liu,Wenrui Hao.An Algorithmic Approach to Finding Factorial Designs with Generalized Minimum Aberration[J].Journal of Complexity,2009,（25）.

[8]马希文.正交设计的数学理论[M].北京：人民教育出版社，1981.

[9]方开泰，马长兴.正交与均匀试验设计[M].北京：科学出版社，2001.

[10]Rainer Storn,Kenneth Prince.Differential Evolution-A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces[J].Journal of Global Optimization,1997,（11）.

（责任编辑/易永生）

TP311.1

A

1002－6487（2010）17-0164-03

韩 冰（1983-），男，江苏南京人，博士研究生，研究方向：飞行仿真。

唐 硕（1963-），男，四川达州人，教授，博士生导师，研究方向：飞行仿真。