不对称血管分支模型
李韶伟
(台州学院 数学与信息工程学院,浙江 临海 317000)
不对称血管分支模型
李韶伟
(台州学院 数学与信息工程学院,浙江 临海 317000)
探讨不对称的血管分支问题,建立关于分支血管半径和分叉角度的一个新的数学模型,利用该模型可验证现有相关结论。
血管分支;数学模型
1 引言
血液循环系统为动物机体输送能量。血液在血管中流动,除了要为血管壁提供能量,还要克服流动阻力。从生物进化的角度,动物血管系统的几何形状应达到最低耗能原则,我们探讨粗细血管的分支模型来满足此原则。文献[1-3]依据对称的几何结构建立模型,并且得到了很好的结论,但依据解剖学的相关文献[4,5]这种几何对称的假设一般不成立,因此,我们有必要探讨不对称的血管分支结构模型。
2 模型假设
2.1 几何假设
如图所示,一条粗血管在分支处分成两条细血管,分叉点附近三条血管共面(这符合生理实际和最优化原则);

图1 血管分支示意图Fig1.Vascular Branches schematic drawing
2.2 物理假设
将血液在血管中的流动视为粘性流体在刚性管道中的运动;
2.3 生物学假设
血液对血管壁提供营养的能量随血管壁表面积
及血管壁的体积的增加而增加;血管壁的厚度与血管半径成正比。由假设1),设单位时间血液在粗细血管中的流量分别为q,q1和q2,则有

由假设2)和Poiseuille定律可得,克服阻力而消耗的能量E1为

一般地,依据假设3)和现有的结论[1],可设供给单位长血管壁营养所消耗的能量为brα(1≤α≤2,b为比例系数).则供给血管壁营养所消耗的能量E2为:

血液从点A流到点B与B′的过程共消耗的能量E为
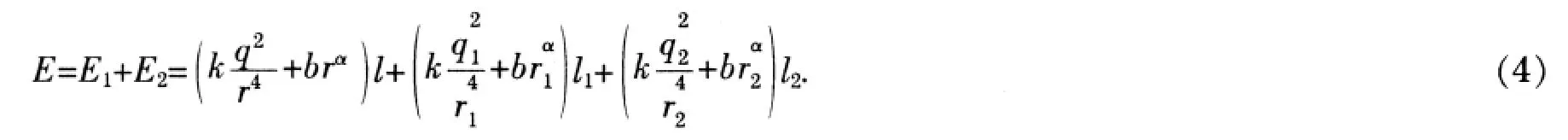
由图1中的几何关系可得:

和

把(5)、(6)式代入(4)式,可得E为关于变量r,r1,r2,θ1,θ2的函数,即

3 模型求解
按函数最优原则,求E(r,r1,r2,θ1,θ2)的最小值点.

4 分析检验
特殊地,当r1=r2时,从(9)、(10)式,可得到几何对称假设下的结论[1-3]

若在(12)式分别取α=1与α=2,则可得r1/r与θ的大致范围

结果与实际情况基本相符。
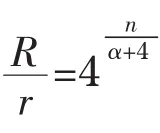

故狗的血管数大约有225~230,如取α=1.5,则有227.5≈1.9亿.
[1]姜启源,谢金星,叶俊.数学模型(第三版)[M].高等教育出版社,2003.
[2]冯元桢.生物动力学-血液循环[M].湖南科学技术出版社,1986.
[3]杨群益.最优血管分支构造[J].青海师范大学学报(自然科学版),2002.(1):68-70.
[4]陈金源,姚班,张玉和.血管分支数学模型的解剖学考证及分析[J].解剖学杂志,1994,17(3):228-230.
[5]谷方,赵琛,龚少兰.腹主动脉及其主要分支的解剖学测量[J].青岛大学医学院学报,2001,37(2):99-100.
An Unsymmetrical Model on the Vascular Branches
LI Shao-wei
(School of Mathematics and Information Engineering,Taizhou University,Linhai 317000,China)
This paper discusses an unsymmetrical Vascular Branches problem, makes a relational model about the radius of vascular branches and the branch angles,then proves existing conclusions.
Vascular Branches;Mathematical Model
O175.2
A
1672-3708(2010)06-0001-03
(责任编辑:耿继祥)
2010-11-05
李韶伟(1979- ),男,浙江仙居人,讲师,博士生,主要从事偏微分方程方面的研究。

