多元函数积分学的教学探讨

张 杰，侯为波

(淮北师范大学数学科学学院，安徽 淮北 235000)

多元函数积分学的教学探讨

张 杰，侯为波

(淮北师范大学数学科学学院，安徽 淮北 235000)

多元函数积分学是数学分析课程教学中的重点和难点.文章从多元函数各种积分概念、各种积分的计算、MATLAB实现三个方面对多元函数积分学的教学进行了初步探讨.

重积分;曲线积分;曲面积分;MATLAB

在数学分析课程的教学中，多元函数的积分学是重点也是难点.它涉及的概念较多，方法公式纷繁复杂，学生往往抓不住要领，计算时无从下手，容易出错.其实，这一部分虽然涉及多种积分，但它们的思想原则是和定积分一脉相承的，都体现了“分割、求和、取极限”的积分思想.因此，在具体教学过程中，只要采用合理的教学方法、积极发挥学生的主观探索意识，就会摆脱困境，获得满意的教学效果.笔者根据这几年来数学分析课程的执教实践，现就多元函数积分学的教学，从以下几个方面谈一些初步体会和想法.

1 多元函数积分的概念

1.1 加强概念的背景知识教学,合理引入概念

在学习一些抽象概念时，学生往往自觉不自觉地要问这些概念有什么用.其实，这正是学生学好这些抽象概念并且掌握它们的巨大动力.在多元函数积分学的定义教学中尤其如此.因此，这要求教学中一定要脚踏实地让学生真切的感受到概念的真实存在性，尽可能向学生展示概念形成和演变的过程，用实例说明可以帮助我们解决生产实践中的那些具体问题.

重积分、第一类曲线、曲面积分的物理背景较简单，分别解决了曲顶柱体的体积、空间立体的质量、空间曲线形构件质量、物质曲面质量的求解问题.下面就第二类曲线、曲面积分概念的教学作一些探讨.在引入第二类曲线、曲面积分概念之前，可以先介绍向量值函数，尽管向量值函数学生以前没有接触过，但掌握起来不算困难.

定义1 n维欧氏空间中点集到 m维欧氏空间中点集的映射，称为向量值函数.一般形式为:

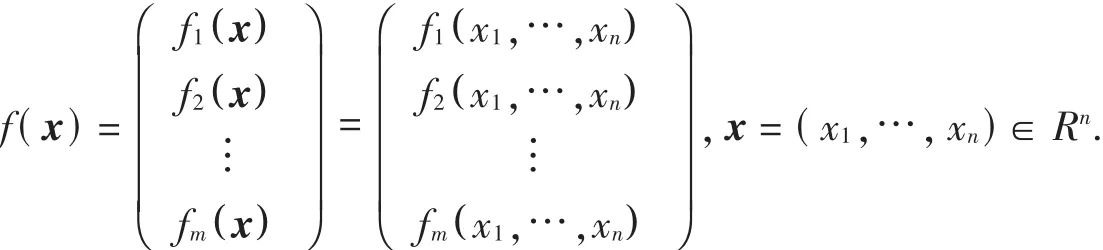
有了向量值函数的概念，就可以借助它讲清楚第二类曲线积分问题的物理背景—— 变力做功问题.据此，也就合理地引出了第二类曲线积分向量形式的定义.

定义2(向量形式) 设 L是从 A点到 B点的光滑空间曲线，向量值函数 F(M)在 L上有定义，用分点A(A0)，A1，…，An－1，An(B)将曲线 L按照从 A到 B的方向任意分割成 n个小弧段 Ai－1Ai(i=1，…，n).记小弧段 Ai－1Ai的长度为 Δsi，并记向量 Ai－1Ai=Δri.在小弧段 Ai－1Ai上任取一点 Mi，作数量积 F(Mi)·Δri，i=1，…，n.令 T=max｛Δsi｝，如果

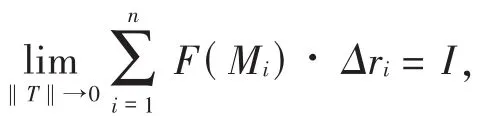
且 I与分割和 Mi的选取无关，则称此极限值为向量函数 F(M)沿曲线 L从 A到 B的第二类曲线积分，记为∫LF(M)·d r.

引入坐标向量，注意到数量积的坐标表示，很自然地就可以得到第二类曲线积分的坐标形式，也就是常见教材中的定义.

定义3(坐标形式) M=(x，y，z)，F(M)=｛P(x，y，z)，Q(x，y，z)｝，R(x，y，z)｝，d r=｛d x，d y，d z｝，则∫LF(M)·d r=∫LP d x+Q d y+R d z.

由于是从问题的实际应用背景出发，上述关于第二类曲线积分概念教学过程思路清晰、条理清楚、便于学生理解记忆.至于第二类曲面积分的概念讲解过程基本和第二类曲线积分类似，只是物理背景变为计算流量问题.

1.2 把握各类积分概念之间的内在联系和区别

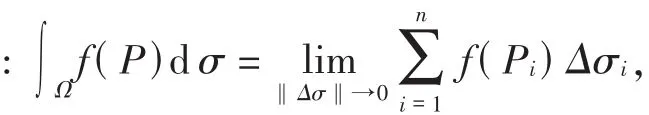
在充分注意各种积分概念共性的基础上，我们也要帮助学生分清楚它们的区别所在，这样在使用各种概念时才不至于混淆.具体来讲就是式∫Ωf(P)dσ中，对不同的积分，Ω代表各种具体的几何形体，dσ代表不同的元素，详见表1.

表1 不同积分 Ω和dσ表示的不同内容

2 各类积分的计算

关于多元函数积分的计算总体思想是转化为定积分.具体方法是:重积分转化为累次积分，曲线积分根据曲线方程直接转化为定积分，曲面积分转化为重积分.在具体计算中，要想顺利计算出正确的结果，要求掌握转化为定积分思想精髓的同时注意换元法、格林公式、高斯公式和斯托克斯公式的合理运用.其实，除了以上基本技能之外，手工计算多元函数积分还有许多技巧可以运用，这些技巧往往可以达到节时省力的效果.下面以常用技巧—— 对称性的运用为例来说明合理运用技巧的意义.

从以上两例可以看到，在计算多元函数积分时，合理运用积分区域的对称性和被积函数的奇偶性，可以大大简化计算.这种技巧总结如下，以供参考.

(1)f(x，y)在区域 D上连续.区域 D关于 x轴对称，且 D1=D∩｛y≥0｝，则

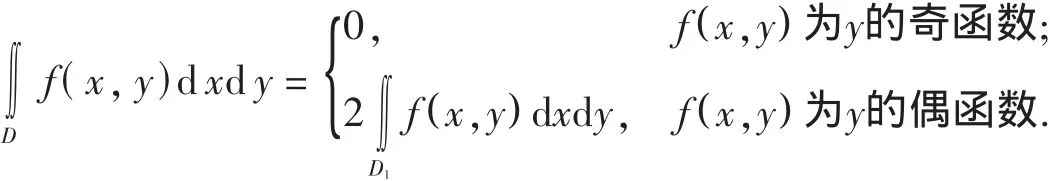
D关于 y轴对称有类似结果.

(2)f(x，y，z)在区域 V上连续.区域 V关于 xoy面对称，且 V1=V∩｛z≥0｝，则

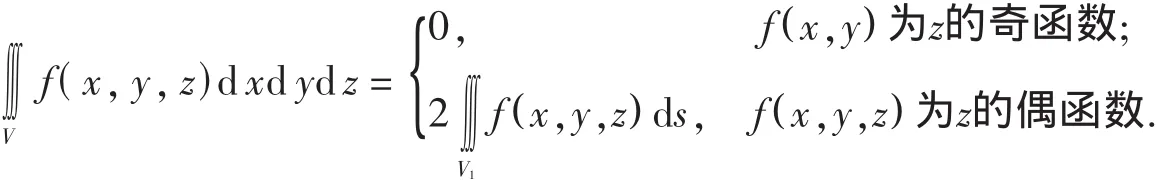
V关于其他两坐标平面对称也有类似结果.

(3)f(x，y)在光滑曲线 L上连续.L关于 x轴对称，且 L1=L∩｛y≥0｝，则

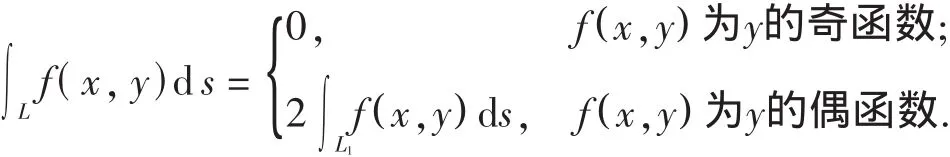
L关于 y轴对称有类似结果.

(4)f(x，y，z)在曲面 S上连续.S关于 xoy面对称，且 S1=S∩｛z≥0｝，则

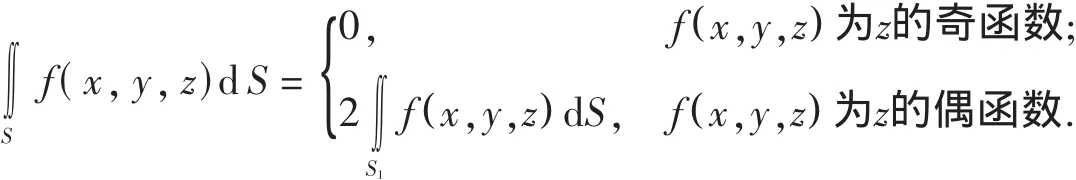
S关于其他两坐标平面对称也有类似结果.

3 MATLAB实现

最后得到所求的近似值为121.665 1.

4 结束语

教学实践表明，科学地安排教学步骤、高效地选择问题的切入点、及时系统地总结知识体系以及有意识地激发学生创造热情对提高教学质量起着至关重要的作用.针对多元函数积分的教学，从概念、各种积分的计算、MATLAB实现三个方面进行了探讨，目的就是尽可能的达到上述目标，从而为提高积分学的教学效果提供有益的参考.

[1]刘寿春.谈多元函数积分学的教学[J].合肥学报学报，2004，14(1):85－87.

[2]许汪涛.谈谈多元积分的学习[J].陕西师范大学继续教育学报，2002，19(3):95－98.

[3]徐虎.多元函数在对称区域上的积分[J].宜宾学院学报，2007，6(6):26－28.

[4]明清河.数学分析的思想与方法[M].青岛:山东大学出版社，2005.

[5]华东师范大学数学系.数学分析(下册)[M].北京:高等教育出版社，2001.

Abstract:Multi－function integral calculus is an emphasis and difficulty ofmathematical analysis.In this paper，we do some preliminary exploration from three aspects which are concepte，calculation method and MATLAB program.

Key words:multiple integral;curvilinear integral;surface integral;MATLAB

Research on Teaching of M ulti-function Integral Calculus

ZHANG Jie，HOUWei－bo
(School of Mathematical Science，Huaibei Normal University，235000，Huaibei，Anhui，China)

O 172.2

C

1672－7177(2010)02－0074－04

2010－01－05

张 杰(1979－ )，女，安徽淮北人，硕士，讲师，研究方向:优化理论.