基于广义形态滤波的图像去噪方法研究

吴时兰， 钱盛友

（湖南师范大学 物理与信息科学学院，湖南 长沙 410081）

0 引言

图像退化的最重要原因就是噪声的加入，因此去噪处理是进行图像分析和识别前的必要步骤。针对不同类型的噪声有不同的去噪方法。通常用均值滤波去除高斯噪声,而脉冲噪声能被中值滤波较好的滤除[1]，但存在细节信息丢失现象,并且在噪声强度大时不能达到很好的去噪效果。近年来由于形态学算子在二值图像处理方面广泛而成功的应用,灰度形态学逐渐成为图像处理领域的一个重要工具。利用形态学开闭或闭开交替滤波器能去除多种类型的图像噪声，但传统的形态学开闭和闭开运算对强噪声污染的图像去噪效果却不理想。现基于形态学理论,对形态学算子进行了改进,并将其用于椒盐噪声的滤除,分析了其去噪效果。

1 灰度图像的形态学处理

1.1 经典灰度形态学的基本理论

在灰度形态学中，最基本的两种运算是膨胀和腐蚀运算,其他形态学变换都是这两种运算根据一定的顺序进行组合的复合运算。

令f (x,y)为灰度图像, b (x,y)是结构元素, Df和Db分别为函数f和b的定义域，采用在定义域中取零的扁平结构元素，则相应的膨胀和腐蚀算子可表示为[2]：

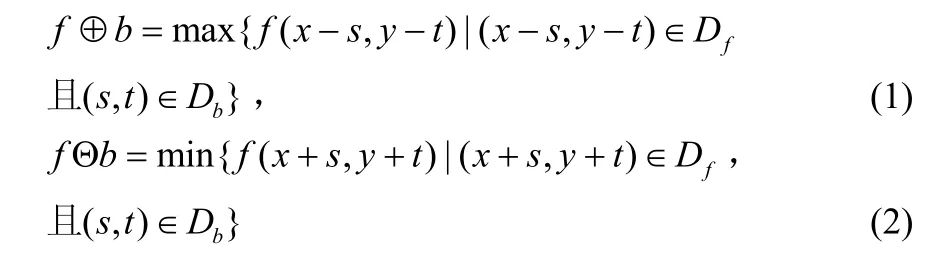
在灰度形态学处理中还有两种非常重要的运算方法：形态开运算和形态闭运算[3]。

开、闭运算分别定义为：

1.2 广义形态学

Maragos利用相同的结构元素，定义了形态开闭和形态闭开滤波器[4]。对于形态开闭滤波而言，首先进行的开运算在去除正脉冲噪声时，同时增强了负脉冲噪声，若再采用相同的结构元素进闭运算，就不能有效地去除全部的负脉冲噪声。同样，采用相同结构元素的形态闭开滤波器也不能有效地去除全部的正脉冲噪声。文献[5]提出了广义的开闭、闭开形态滤波。

广义的形态开闭滤波和闭开滤波的定义为：

b1，b2为两个结构元素，且 b1⊆b2。

广义的开闭和闭开运算能较好的去处脉冲噪声[5]。对当图像被强噪声污染时，这种方法却得不到很好的去噪效果。

1.3 改进的广义形态学

开运算是先腐蚀后膨胀。当图像被盐噪声污染时，利用腐蚀运算，盐噪声可以被图像的灰度值代替，即盐噪声被有效地滤除；当图像被椒噪声污染时，利用膨胀运算，椒噪声可以被图像的灰度值代替，即椒噪声被有效地滤除。当噪声强度大时，在一个小小的邻域中有可能都是被噪声污染的图像信息。当运用腐蚀运算时，盐噪声极有可能被椒噪声代替，出现更糟的情况是图像信息被椒噪声代替；而当运用膨胀运算时，椒噪声极有可能被盐噪声代替，甚至出现图像信息被盐噪声代替的糟糕情况。因此，噪声强度大时，运用开闭、闭开运算不能有效地去除噪声，甚至有可能使图像变得更糟糕。

1.3.1 改进的腐蚀运算和膨胀运算

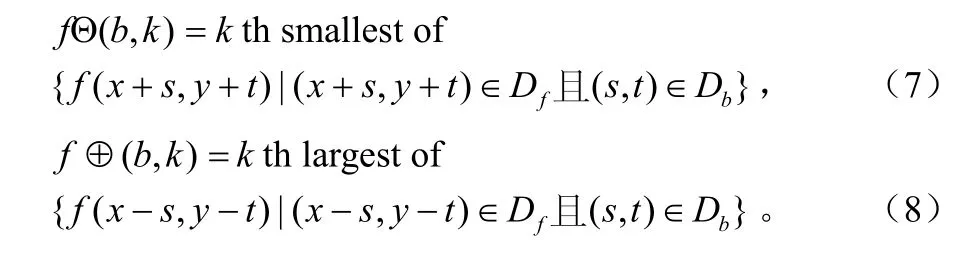
改进的腐蚀运算不是用像素邻域的最小灰度值代替该像素的灰度值，而是用该像素邻域的第k个小值取代该像素的灰度值。当图像被高密度的盐噪声污染时，运用改进的腐蚀运算，盐噪声极有可能被图像信息取代，即有效地去除了亮噪声。同理，改进的膨胀运算能有效地去除椒噪声。

1.3.2 改进的广义开、闭运算

改进的广义开运算定义为：

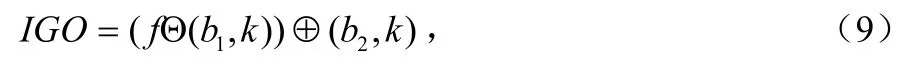
改进的广义闭运算定义为：

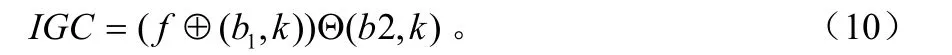
1.3.3 改进的广义形态学滤波

中值滤波、形态滤波对图像的每一个像素都要进行处理，这样有可能使不含噪声的图像的灰度值被相邻点的灰度值代替，使图像变得模糊，且去噪时间较长。

这里先确定被污染图像中的各个像素是否被噪声污染，依据像素是否是该邻域（其中邻域采用 3×3的方形窗口）的最大值或最小值来确定该像素是否被噪声污染。如果是的话，就认为该点被噪声污染，再对被污染点采用改进的广义形态学滤波；如果不是的话，就认为这点没有被噪声污染，不对它进行处理。

2 仿真实验及结果分析

在实验中使用205 px×232 px的“tire.tif”的图像，分别加入噪声强度为 0.1～0.8的椒盐噪声。通过仿真发现，当噪声强度为0.5时，k取4时去噪效果最佳。这里的滤波方法与广义形态滤波、3×3中值滤波、5×5中值滤波进行了比较，结果如图1所示。从图1可以看出：在图像噪声强度大时，广义形态滤波和3×3中值滤波的去噪效果非常差，5×5中值滤波不能完全去除噪声，而提出的方法滤波效果较好。为了判定这几种方法的好坏，可以用评价图像质量的客观标准峰值信噪比（PSNR）、均方误差（MSE）来衡量各种方法的去噪效果。其结果如表1所示。

图1 噪声强度为0.5时不同方法的滤波效果

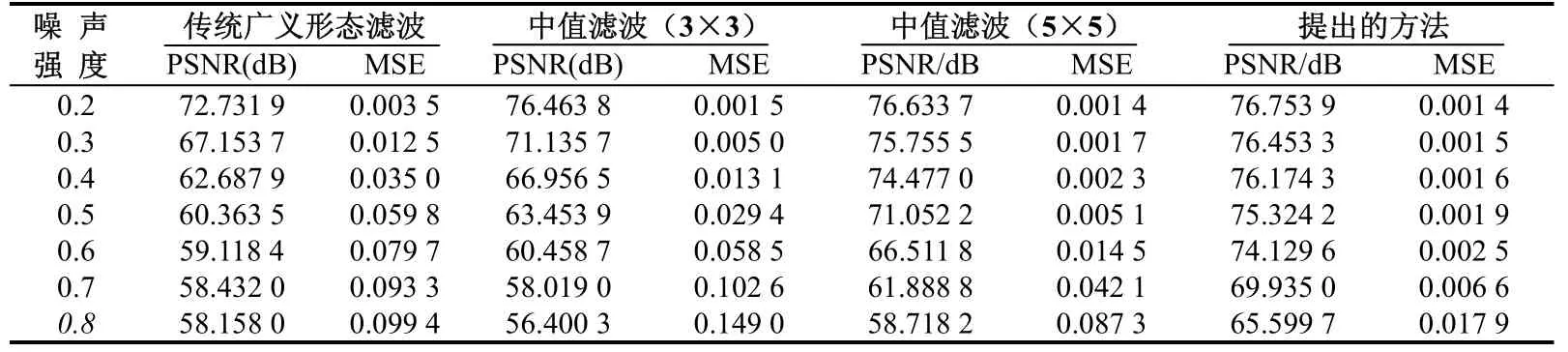
表1 去噪图像的峰值信噪比和均方误差

从表 1中可以看出，这里的方法的去噪效果优于其它 3种方法，当噪声强度愈大时，这里的方法的优势愈明显。

3 结语

针对传统的形态滤波方法在噪声强度大时去噪效果差的缺陷，提出了一种改进的广义形态滤波方法。首先依据像素是否是该邻域的极值来确定该像素是否被噪声污染，然后对被噪声污染的像素进行改进的广义形态滤波。因为不需要对每个像素进行处理，所以滤波时间被缩短。用该方法对含不同强度椒盐噪声的图像进行了处理，并与其它方法进行了比较。仿真结果表明，在强噪声情况下，提出的方法在视觉效果和图像质量客观评价指标上均优于传统形态学滤波和中值滤波。相对原始无噪图像，去噪后的图像有些模糊。怎样在既能滤除噪声的同时又能有效地保持细节，是下一步研究的方向。

[1] 董汉磊，徐利平，高颖敏，等.基于Bior小波变换和中值滤波的图像去噪[J].通信技术，2009, 42(11)：171-175.

[2] 杨征宇,夏庆观.形态学算法的去噪处理在自由曲面重构中的应用[J].模具工业，2009,35(09)：22-25.

[3] 乔德江，陈鸿昶.基于数学形态学的模糊子笔画提取[J].通信技术,2009,42(02)：174-178.

[4] 崔屹.图像处理与分析数学形态学方法及应用[M].北京：科学出版社,2000：98-135.

[5] 白银刚,于盛林,李建明.一类新的广义开和广义形态闭滤波器[J].中国图像图形学报，2009,14(08)：1523-1529.