矩阵求逆的 FPGA实现

李涛, 张忠培

(电子科技大学通信抗干扰技术国家级重点实验室,四川 成都 611731)

0 引言

矩阵求逆在低密度校验(LDPC)编码,多输入多输出正交频分复用(MIMO-OFDM)等领域有着重要的作用,即是应用于 MIMO-OFDM系统中对多径衰落信道进行信道估计。目前,矩阵求逆大都是用软件实现,在低速通信的情况下基本能满足要求,但在高速通信领域,软件运算速率低的弊端严重影响其应用,这就要求在已有软件算法的基础上用FPGA加以实现。

目前已有文献提出对三角矩阵求逆的硬件实现方法[1],但很少有对任意矩阵求逆的硬件实现方法的研究。现结合已有三角矩阵求逆的硬件实现方法和矩阵的 LU分解算法,提出了一种对任意满秩矩阵求逆的硬件实现方法。VHDL代码采用流水线操作,并利用 MAC(乘累加)单元,使系统工作频率得到了进一步提高,系统工作频率达到100 MHz以上。

1 理论分析

矩阵的一种有效而广泛应用的分解方法是矩阵的 LU三角分解,将一个n阶矩阵A分解为一个下三角矩阵 L和一个上三角矩阵U的乘积。利用上下三角矩阵求逆的便利性来得求任意n阶矩阵A的逆矩阵可大大减少运算量和复杂度。具体的流程为：首先对矩阵进行 LU分解,接着对 L和 U矩阵求逆得到L-1和 U-1,再利用矩阵乘积求得原始矩阵 A的逆矩阵 A-1=U-1L-1。

1.1 矩阵的LU分解

若 n阶方阵 A∈Cn*n

n的各阶顺序主子式不等于零,即：

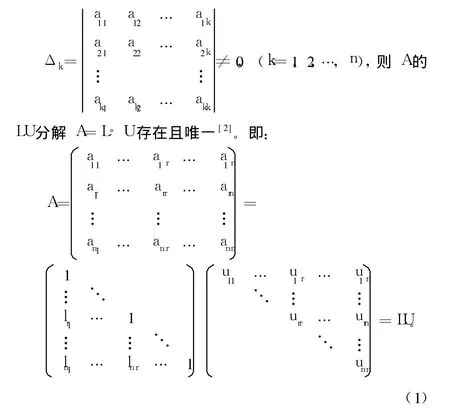
由矩阵的乘法原理,可推导出LU分解的迭代算法[3]：

矩阵的LU分解是一个循环迭代的过程,U矩阵是从第 1行迭代到第n行,而 L矩阵则是从第 1列迭代到第n列,且U矩阵先于 L矩阵一个节拍。

1.2 L矩阵和 U矩阵求逆

首先假设下三角矩阵 L的逆矩阵为R,不失一般性,考虑 4阶的情况,利用 LR=I有：

从而求得下三角矩阵L的逆矩阵 R式(4),同样的方法可以求出 U矩阵的逆矩阵。

首先,利用原始矩阵 L求出逆矩阵 R的斜对角元素 rii。接着,利用原始矩阵L和已求出的逆矩阵的斜对角元素求出与斜对角元素相邻的斜列 rj,j-1,依次循环,迭代 n-1次,求出整个逆矩阵R。

1.3 矩阵相乘

上三角矩阵U的逆矩阵V与下三角矩阵L的逆矩阵 R相乘,最终得到原始矩阵 A的逆矩阵 A-1=U-1L-1=VR,完成整个矩阵求逆的过程。

2 FPGA实现

与理论算法对应,硬件实现电路包括 3个主要模块：LU分解、上下三角矩阵求逆和矩阵相乘。硬件系统结构如图 1所示。

图 1 硬件系统结构

功能描述：

① Invmatrix_top：顶层模块,控制整个系统的时序逻辑;

② LU：LU分解模块,将输入到 RAM的数据进行 LU分解,结果存储进 RAM;

③ Inverse_matrix：求逆模块,分别计算出 L和 U的逆矩阵R和V;

④ Multi：乘法模块,R和 V相乘,得到 A的逆矩阵,并将结果存入RAM;

⑤ RAM：存储模块,随机存取存储器。

2.1 LU分解模块

根据式(2),采用 VHDL硬件描述,在赛灵思(XILINX)的xc4vlx80-12ff1488型号 FPGA布局布线下,采用 ISE仿真,系统工作时钟能达到 100 MHz以上(约 153.726 MHz)。4◦4矩阵的 LU分解仿真结果如图 2所示。

其中,rst为复位信号,clk为输入时钟,start为模块使能信号,din为输入数据,edone和done分别为输出使能提前标志位和使能标志位。

输入数据 A为{1 0 1 2;1 4 2 2;0 2 3 2;4 1 3 5},输出数据 L为{1024 0 0 0;1024 1024 0 0;0 512 1020 0;4096 256-510 1026},U为{1024 0 1024 2048;0 4096 1024 0;0 0 2560 2048;0 0 0-2052}。输出数据与理论值相符,因为 FPGA不能处理浮点数,所有数据均为理论值的倍。输出数据宽度为20,包括 10位整数位和 10位小数位[3]。

图 2 LU分解模块仿真波形图

2.2 求逆模块(Inverse_matrix)

求逆模块也是一个乘累加过程,首先计算出斜对角元素,再依次求出紧邻的斜列元素[4]。整个模块分为 RAM存储单元,乘累加单元和下标控制单元。求逆模块结构图如图3所示。

图3 求逆模块结构

其中,MAC单元的 VHDL代码优化方法与 LU分解代码优化方法相同,具体控制参考 1.2节所述下三角矩阵求逆运算流程。

2.3 Multi矩阵乘法模块

矩阵乘法模块的输出即为最终输出。整个系统的延迟等于三个模块——LU分解模块,三角矩阵求逆模块和矩阵乘法模块的延迟之和,需要 ramu_quot的位宽与 ramu_remd位宽之和的 N+1倍时钟周期,其中 LU分解需要ramu_quot的位宽与 ramu_remd位宽之和的N倍时钟周期,矩阵求逆模块需要 ramu_quot的位宽与 ramu_remd位宽之和的 1倍时钟周期,乘法模块采用流水操作时为及时输出,延迟为零。

3 实验仿真结果分析

软件程序的编写和仿真采用 Mathworks公司的 MATLAB R2008b[5]软件环境。输入矩阵

,软件仿真输出的逆矩阵INV_A为式(5)：

硬件仿真采用 Mentor公司的 Modelsim SE 6.2b,电路的FPGA综合采用 Xilinx ISE 7.1i。硬件仿真波形输出如图4所示。

仿真波形表明,硬件仿真结果与软件仿真结果吻合。因硬件无法处理小数,所有数据均换算为整数进行计算,输出值为理论值的 210倍,输出高 10位表示整数部分,输出低 10位表示小数部分。部分值与理论值存在微小偏差,原因是硬件仿真采用定点仿真算法,软件仿真采用浮点仿真,定点时数据位的截断产生了误差。

图 4 矩阵求逆系统硬件仿真波形

4 结语

通过对矩阵矩阵求逆算法的理论分析,分别阐述了 LU分解、三角矩阵求逆和矩阵乘法的算法实现和硬件实现方法,再用MATLAB和Model Sim分别对软件和硬件代码进行了仿真,利用仿真结果对比分析,验证了硬件实现的正确性。

由于充分利用了硬件的速度优势,矩阵求逆的 FPGA实现非常适合于现代数字通信领域。现已用于实际项目中,对多点协作(COMP)条件下 MIMO-OFDM系统的多径衰落信道的信道矩阵求逆,实时进行信道估计。

[1]董永胜.一种整数矩阵求逆方法的证明 [J].长春师范学院学报,2008,16(02)：4-5.

[2]黄廷祝,钟守铭,李正良.矩阵理论[M].北京：高等教育出版社,2007.

[3]李增喜.LDPC一致校验矩阵的 LU分解算法[J].通信技术.2009,42(01)：126-127.

[4]李颖异.中国有线电视 [EB/OL].(2006-07-01)[2010-02-11].http：//scholar.ilib.cn/A-QCode～zgyxds200607018.html.

[5]电子科技大学应用数学学院.MATLAB编程技术与数学试验[D].成都：电子科技大学出版社,2006.