基于循环谱的MPSK信号识别
何 为, 高 峰, 李跃波, 刘 锋, 黄刘宏
(①总参工程兵科研三所,河南 洛阳 471023;②黑龙江省人防设计研究院,黑龙江 哈尔滨 150000)
0 引言
目前,针对循环平稳信号的信号处理技术是现代信号处理领域中的热点问题之一[1]。在文献[2]中,Gardner系统地建立了循环平稳过程的表示方法,并相继提出了循环平稳过程的谱相关理论及其信号谱相关分析技术。MPSK信号是一类载波受抑制的相位调制信号,它们具有相位连续,幅度恒定的特性。MPSK信号在通信的很多领域都有广泛的应用,常用的有二进制数字相位调制(BPSK)、四进制数字相位调制(QPSK)以及八进制数字相位调制(8PSK)等信号。针对MPSK信号的调制识别对电子战与信息战中的信号侦察,民用中的通信信号认证、干扰识别、频谱管理等方面,都具有非常重要的意义[3]。对MPSK信号谱相关特性进行了深入的分析,提出了一种基于循环谱的 MPSK信号调制识别算法,并对算法进行了分析,在Matlab环境下对其性能进行了仿真验证。
1 谱相关的定义
随机信号 ()x t的自相关函数定义为:
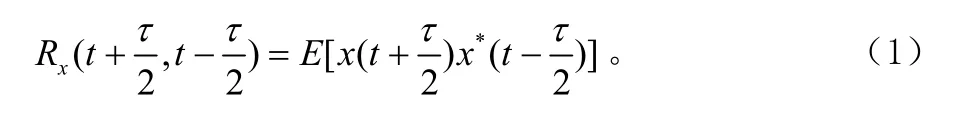
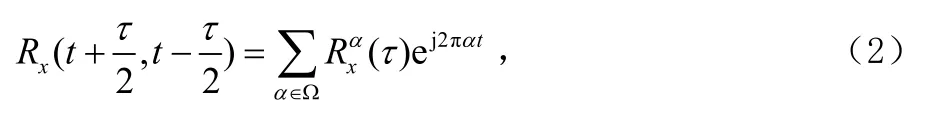
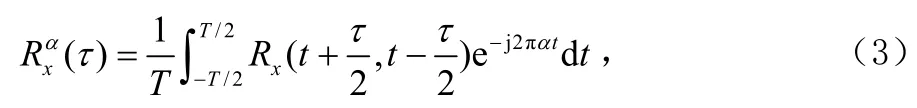
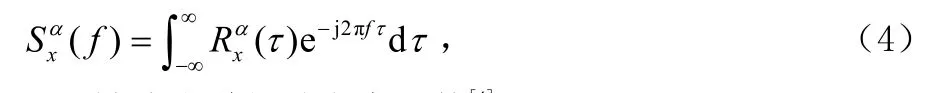
2 MPSK信号的谱相关分析
BPSK可以表示为[5]:
其中:

其它参数说明同上。文献[6]推导出 BPSK信号的循环谱密度为:
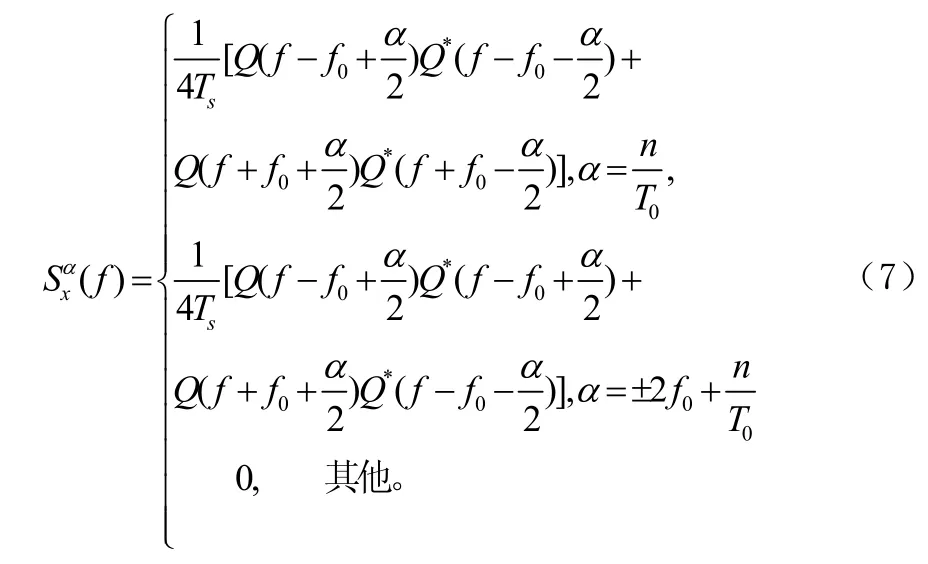
假设信号初始相位为零, Q ( f)为成形脉冲 q ( t)的傅立叶变换,代表共轭。在和处谱相关(f)会有明显的谱峰出现。
同理,MPSK信号( M ≥ 4 )可以表示为:
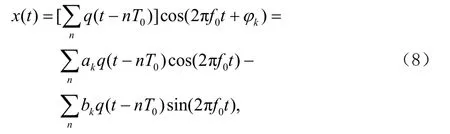
式中φk为被调相位,可以有M(M≥4)种不同取值,ak=cosφk;bk=sinφk。MPSK信号(M≥4)的循环谱密度为:
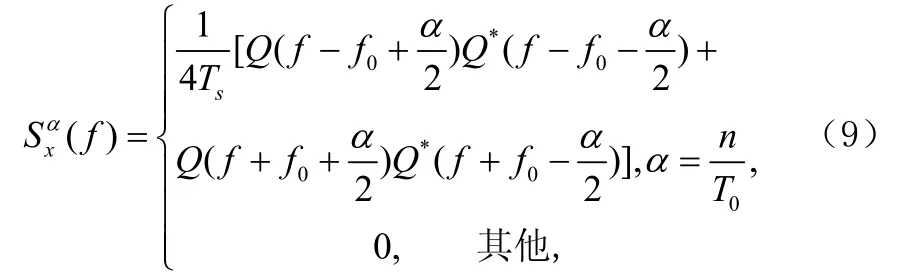
如果{ak}和{bk}是平稳序列,则仅在(n为整数)时,(f)有峰值。
3 MPSK信号的调制识别
以BPSK、QPSK和8PSK为例,上节式(7)和式(9)中令00f= ,则可以得到三种信号的 0f= 的循环频率截面(以下简称 0f= 截面)图如图1、图2和图3所示。
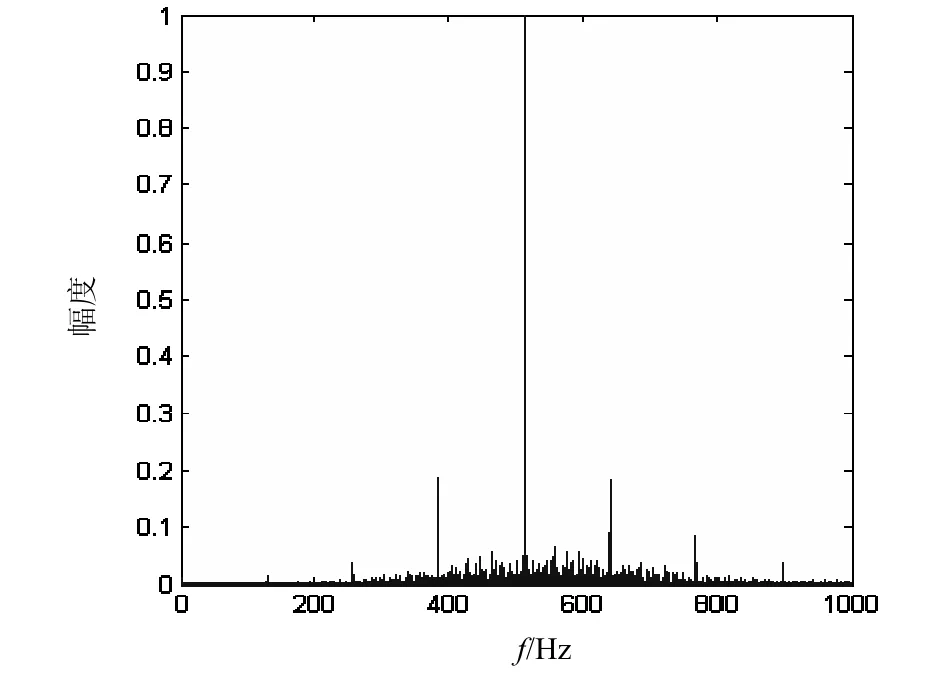
图1 BPSK信号循环谱f=0截面
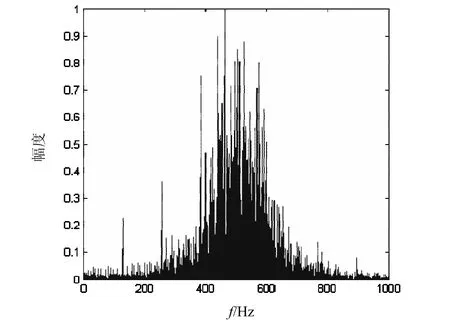
图3 8PSK信号循环谱f=0截面
可以看出,BPSK信号的f=0截面次大值与QPSK和8PSK信号在该截面的次大值有着明显区别,分别以这三种信号在f=0截面的最大值与次大值的比值为特征,得到特征曲线如图4所示。
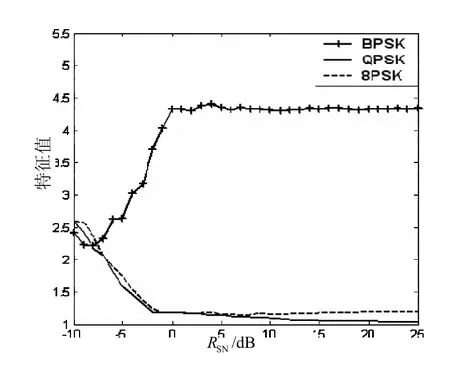
图4 BPSK、QPSK和8PSK信号循环谱f =0截面特征仿真
通过仿真可以看出,该特征在信噪比-5 dB以上明显并随着信噪比的提高最终收敛;只要设置合理的特征门限就可以首先识别出BPSK信号。
下面分析QPSK与8PSK信号的识别;MPSK( 4M≥ )信号可以表示为:将其平方得:
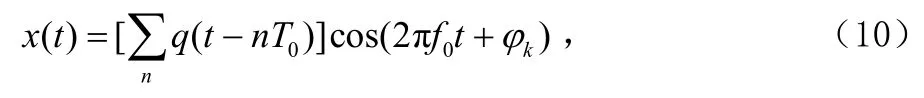
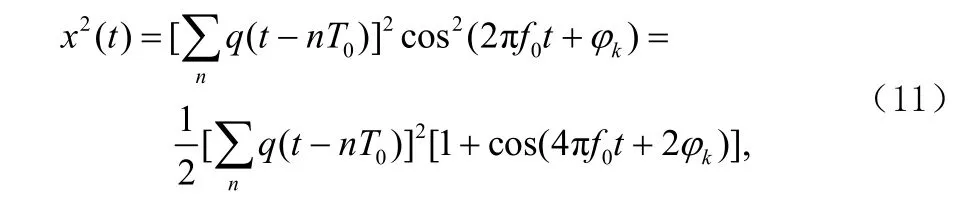
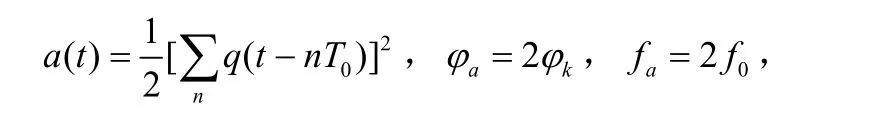
令:则有:

C( t)与φa和fa无关,可以当做随时间变化的噪声。因此由式(12)得出M( M ≥ 4 )阶PSK信号经过一次平方后降为M/2阶PSK信号。
将QPSK与8PSK信号分别平方后,对其 f = 0 截面特征做仿真得到特征曲线如图5所示。
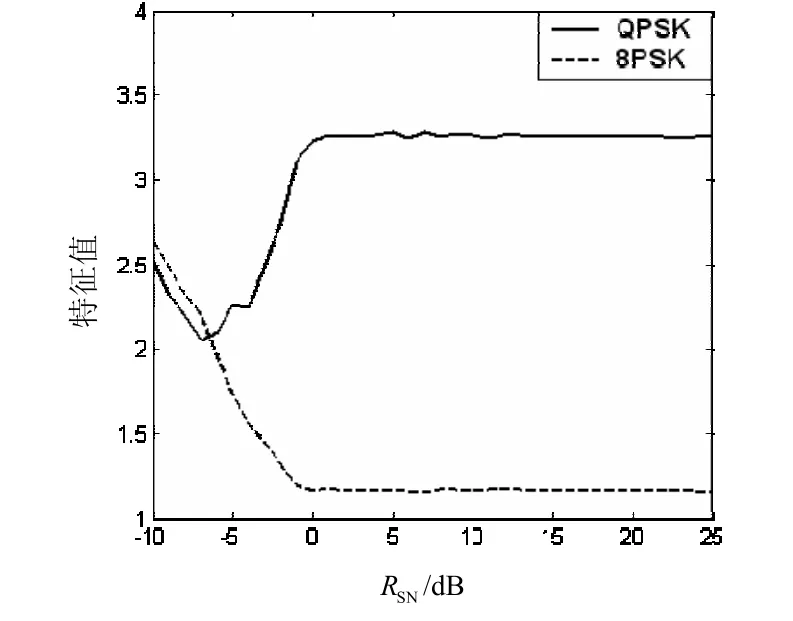
图5 QPSK和8PSK信号平方后循环谱f =0截面特征仿真
通过仿真可以看出,平方后QPSK与8PSK信号的 0f= 截面特征在信噪比大于 0 dB时稳定并最终收敛。因此,对于QPSK与8PSK信号的识别,首先将信号平方降阶,把对QPSK与8PSK信号的识别转化为对BPSK与QPSK信号的识别,然后通过提取信号的 0f= 截面特征,即可区分出原 QPSK和8PSK信号。其它高阶MPSK信号的子类识别方法以此类推。
4 算法仿真
按照前面的调制识别算法步骤,在 Matlab环境下对其进行仿真验证。MPSK信号源分为BPSK、QPSK和8PSK三种,载频cf=4 kHz,波特率Rb=1 kHz,信号采样速率sf=16 kHz,响应时间st=1 s,在高斯白噪声环境下对其进行了 2000次蒙特卡洛仿真,得到了MPSK信号调制识别率曲线图如图6。
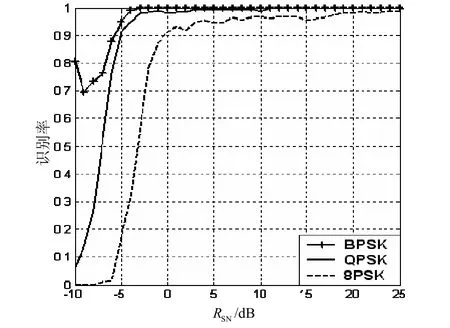
图6 MPSK信号识别率曲线
由仿真可以看出,在信噪比高于 0 dB时,识别率达到85%以上;随着信噪比的提高,识别性能会明显提高。在信噪比高于5 dB时,MPSK信号的整体识别率高于95%。
5 结语
通过对 MPSK信号谱相关特性的分析,提出了一种基于循环谱的 MPSK信号子类识别算法,并进行仿真分析,仿真结果表明,该算法在信噪比5 dB以上识别率高于95%。该算法可推广至所有 MPSK信号的子类识别。需要注意的是,将MPSK信号平方后会产生交叉项随着 MPSK信号阶数的提高,该算法对信号所需平方次数也会相应提高,在本质上降低了高阶 MPSK信号的信噪比,因此,对于高阶MPSK信号,该算法对信噪比会提出更高的要求。
[1] GARDNER W A. Exploitation of Spectral Redundancy in Cyclostationary Signals[J]. IEEE SP MAG,1991(04):14-36.
[2] GARDNER W A.Statistical Spectral Analysis: a Non- probabilistic theory [M]. NJ:Prentice-Hall, 1988.
[3] 罗利春.关于谱相关的几个问题——II:物理功能与应用效果[J].电子对抗,2002(03):18-25.
[4]田鹏武,袁佳,于宏毅.基于循环谱的 MSK信号参数估计[J].通信技术,2008,41(01):9-11,17.
[5] 樊昌信,詹道庸,徐炳祥,等.通信原理[M].北京:国防工业出版社,2001:132-133.
[6] GARDNER W A.Measurement of Spectral Correlation[J].IEEE Trans.Acoust, Speech, Signal Processing,1986,34(05):1111-1123.

