服务设施选址的博弈分析
孟尚雄
(北京物资学院经济学院,北京市101149)
服务设施选址的博弈分析
孟尚雄
(北京物资学院经济学院,北京市101149)
市场除具有网络特征外,还具有明显的层次嵌套特征。文章结合这两个方面的特征,对具有层次嵌套特征的人口、市场空间分布条件下服务设施的选址博弈问题进行了研究。结果发现,两个企业的服务设施竞争选址静态博弈,可以不存在纳什均衡;在纳什均衡存在的情况下,并不能保证双方市场份额相等;市场层次嵌套特征在一定程度上破坏均衡的存在,内层市场较大的市场份额吸引着对手进入,使外层市场均衡受到破坏;增加服务设施可以扩大市场覆盖范围,但由于利润最大化目标和距离的约束,在给定市场环境下,有些市场区域可能永远无法覆盖。
选址问题;纳什均衡;聚类分析;层次嵌套
一、引论
经典的选址问题是,对于给定的需求或顾客,厂商如何选择其新设施的最优位置来获取最大利润。当厂商多于一个时,为争夺给定的需求,它们必然相互竞争抢占有利位置。对竞争选址问题较早的研究包括霍特林(Hotelling)于1929年对竞争稳定性的分析。[1]此后,许多不同领域的学者进一步研究了竞争选址模型,内容涉及空间经济和工业组织、[2]、[3]数学、[4]运筹学[5]、[6]、[7]等诸多学科。关于这一研究领域的综述可以参考艾赛特(Eiselt)等的研究。[8]
博弈论是研究竞争选址问题的一个有效工具。安恩(Ahn)等运用博弈论研究了线段和圆周上的竞争选址问题;[9]马沙诺夫和萨卡古茨(Mazalov &Sakaguchi)研究了平面上的双头垄断模型。[10]然而,现实的经济活动区域并非规范的点、线或面,人口和市场很少按照简单几何体的规律进行空间分布。一个较为贴近现实的选址博弈是高西和克雷德(Ghosh&Craig)的两个零售商在竞争市场中的选址,[11]他们把市场表示为一个网络。实际上,市场除具有网络特征外,还具有明显的层次嵌套特征。这一点早就被克里斯塔勒(Christaller)[12]和罗煦(L觟sch)[13]研究的中心地理论所证实了。
本文将这两方面的特征结合在一起,研究了具有层次嵌套特征的人口、市场空间分布条件下的服务设施选址博弈问题。首先,给出一般市场的层次嵌套表示;对层次嵌套市场的市场份额分配进行必要的讨论;在此基础上进一步讨论企业和消费者的约束。其次,描述服务设施选址博弈模型,包括收益矩阵的形成和均衡解的讨论。最后,对几种典型博弈模型解的实际意义进行分析。
二、市场特征
1.层次市场。竞争选址模型讨论的市场指消费者的空间分布范围。霍特林模型的市场是线性市场,也就是消费者均匀地分布在一条线段上。同样,安恩及其他学者的模型假定市场是圆周或平面,消费者在这些几何体上均匀分布。高西和克雷德的模型假定消费者分布在网络的节点上。然而,现实中的市场经常带有层次特征,也就是消费者的空间分布具有底层、高层等多种层次。例如,消费者的空间分布可以在社区、乡镇区域、县级区域、市级区域、省级区域等多级层次上分别或同时讨论。这些不同层次的区域都是由消费者所处的基本需求点(如街道、村落)构成的。研究对象不同,所关注的市场层次也不一样。有时,只关注某一层次的市场就可以,比如对于一些日常生活用品,只要考虑乡镇或社区一级的市场就足够了;而有时,则必须同时考虑多个市场层次,比如对于一些高档商品,必须同时考虑市级和省级高层市场。为便于进行一般性研究,需要对一个经济的市场进行分层表示。
假设一个经济包含N个基本需求点,它们构成的集合为C={C1,C2,…,CN};每个基本需求点包含若干消费者,消费者数目构成的集合为R= {R1,R2,…,RN};基本需求点Ci、Cj之间的距离为dij。那么,消费者的空间分布就完全由C、R和d..确定。基于C和d..,可应用聚类分析法产生系统聚类图,使用这种聚类图可以较好地描述市场的层次嵌套特征。[14]
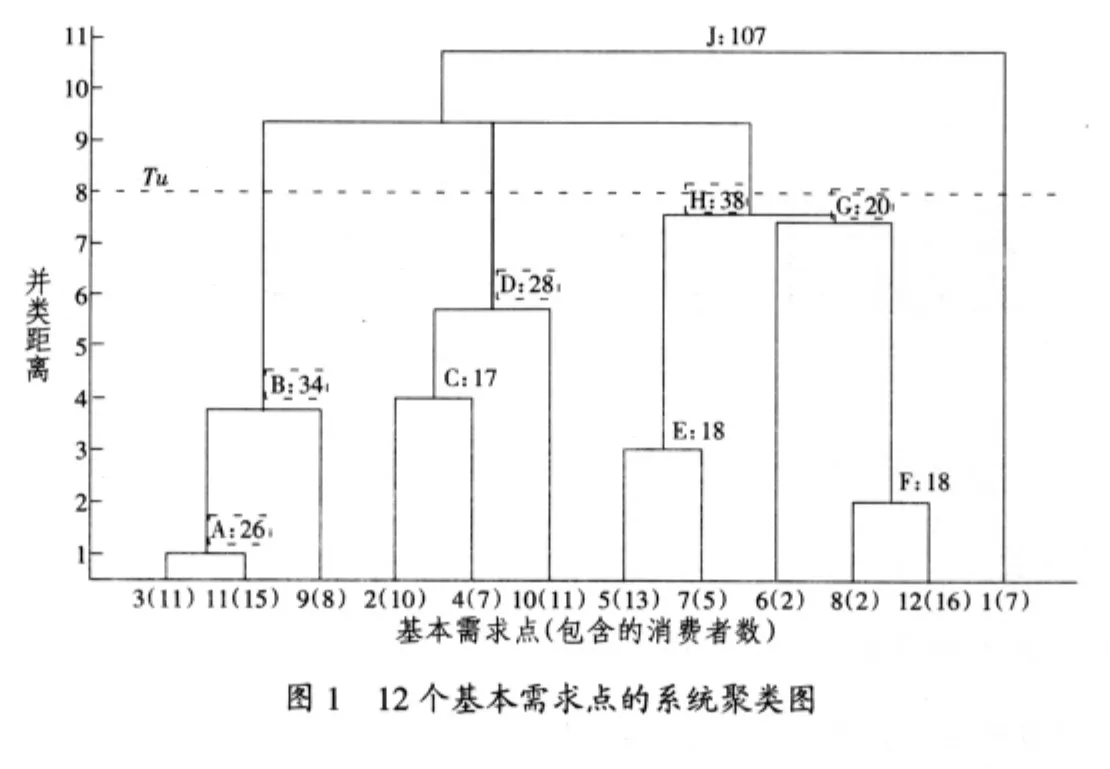
图1表示由12个随机产生的基本需求点形成的系统聚类图。纵轴为并类距离,反映了在形成各个层次的市场时,消费者之间的平均距离;横轴为基本需求点,括弧内的数字代表相对应的基本需求点所包含的消费者人数。在这个由12个基本需求点所构成的市场内,12个基本需求点是最基本的市场单位(可以对应社区),A~J等表示9个更高层次的市场区域(可以对应街道、区、乡镇等,也可以不对应行政区划,而对应自然形成的更高层次的市场区域),它们具有不同的层次、不同的大小,并存在不同层次的区域嵌套现象。例如,市场A嵌套在市场B里面,B是比A层次更高的市场;市场F、E、G嵌套在市场H里面,F、G、H的市场层次一个比一个高。J是层次最高的市场,12个基本需求点是层次最低的市场。每个市场的规模由它所包含的消费者数量的多少确定,市场符号旁边的数字代表市场的规模,如市场B的规模是34,市场A的规模是26。市场B的规模由它所包含的三个基本需求点3、11、9所包含的消费者数11、15、8相加而得。
2.市场份额的分配原则。如果消费者总是选择最近的服务设施进行消费(就近选择原则),那么市场的层次嵌套特征对设施的市场份额产生这样的影响:
(1)嵌套分配。当两个企业的服务设施所处的市场具有嵌套关系时,建立在低一层次市场的设施会占有高一层次市场设施的市场份额。例如,若企业Q1在市场A建立一个设施,企业Q2在市场B建立一个设施,那么企业Q1的市场份额是26,企业Q2的市场份额是8而不是34。
(2)同层分配。当两个企业的服务设施处于同一层次的市场时,它们平分市场份额。例如,如果企业Q1和Q2在市场A分别建立一个设施,那么它们各自的市场份额都是13。
(3)无嵌套分配。如果两个企业服务设施所处的市场不存在嵌套关系,则它们分别得到自己所在市场区域的全部市场份额。例如,若企业Q1在市场A建立一个设施,企业Q2在市场D建立一个设施,那么Q1的市场份额是26,Q2的市场份额是28。
3.成本门限与最低需求。为保证足够的利润,除选择有利的设施位置外,所建立的服务设施还必须覆盖一定数目的消费者以弥补其经营成本。因此,企业心目中都有一个保留的成本门限,表现在市场上,就是要有一个最低的消费者覆盖数目,比如RL=20,以弥补其成本门限。也就是说,企业只有能够覆盖20个单位以上的消费者时,才有动机建立一个设施来提供服务,这可以看成企业所面对的一种需求约束。图1中的A、B、D、G、H、J满足这一需求约束。如果一个企业想同时建立多个设施,我们假定只要平均每个设施满足需求约束,企业的需求约束就得到满足。例如,若企业想建立两个设施,第一个设施覆盖的需求只有11个单位的消费者,而第二个设施覆盖了32个单位的消费者,那么对企业来说,尽管第一个设施覆盖的需求小于RL=20,但由于两个设施覆盖的总需求43(11+32)大于2RL=40,即平均每个设施覆盖的需求21.5(43/2)大于RL=20,企业的需求约束就可以得到满足。
4.消费者距离约束。对消费者而言,为得到某种服务,必须行走一定距离的路程,不过他们也不想走得太远去进行消费。因此,消费者有一个能够容忍的最大的平均距离,比如Tu=8。也就是说,消费者为了得到某种服务,愿意行走的最远距离平均不会超过8个单位,这可以看成消费者的距离约束。这里之所以考虑平均距离,是因为所研究的消费者是基本需求单位或更高层次市场中所有的消费者,而不是单个消费者。各层次市场消费者的距离约束用平均距离较为合理。
于是,带有需求约束和距离约束的系统聚类图就把市场的基本环境展现了出来,用En(C,R,d..|RL,Tu)表示系统聚类图所展示的市场基本环境。
三、服务设施选址博弈模型
考虑两个企业Q1、Q2在市场环境En(C,R,d..|RL,Tu)中建立服务设施为消费者提供服务,以谋求利润最大化。具体假设如下:
第一,它们建立一个服务设施的成本相同,并且提供相同的服务。
第二,消费者选择最近的设施进行消费,即遵循就近选择原则,从而低层次市场区域所建立的设施会占有高层次市场区域所建立设施的市场份额。
第三,每一层次的市场只有一个最优位置,在这个位置上每个企业最多建立一个设施,但可以有多个企业在这个位置上建立设施。
第四,在同一个市场位置建立的设施平均分配这一市场份额。
第五,市场受需求约束(消费者最低覆盖数RL)和距离约束(消费者愿意行走的最远距离Tu)的限制。如果RL=20,Tu=8,那么在图1表示的市场环境En(C,R,d..|RL,Tu)中,只有A、B、D、G、H五个市场区域满足这些条件,这也是所有可供两个企业选择的区域。本文假定企业Q1、Q2同时采取选址行动,下面对它们建立不同数目设施的几种静态博弈进行讨论。
1.(1,1)博弈。假定企业Q1、Q2打算在给定的市场环境中各自建立一个服务设施,即(1,1)博弈。企业Q1、Q2的收益矩阵由各自的市场份额来表示,具体份额大小如表1所示。其中市场份额的分配按照前面所述的嵌套分配、同层分配、无嵌套分配等三种市场份额分配原则进行。
不难看出,此时的博弈存在两个纳什均衡:Q1选择在市场B建立设施,Q2选择在市场H建立设施;或Q1与Q2互相调换位置。它们所获得的市场份额分别为34、38个单位,所覆盖的总的市场份额为72个单位。
2.(2,1)博弈。假定企业Q1打算在给定的市场环境中建立两个服务设施,按照前面的假定,只要这两个设施能够覆盖的消费者不少于2RL=40个单位,平均每个设施覆盖的消费者就能够达到RL=20个单位,企业的需求约束就能够得到满足。假定企业Q2打算建立一个服务设施,其条件与前面相同。那么,企业Q1、Q2的收益矩阵如表2所示,对应的博弈存在三个纳什均衡:
(1)Q1选择在市场B、D建立两个服务设施,获得62个单位的市场份额;Q2选择在市场H建立一个服务设施,获得38个单位的市场份额。它们所覆盖的市场总份额为100个单位。
(2)Q1选择在市场B、H建立两个服务设施,获得72个单位的市场份额;Q2选择在市场D建立一个服务设施,获得28个单位的市场份额。它们所覆盖的市场总份额为100个单位。
(3)Q1选择在市场D、H建立两个服务设施,获得66个单位的市场份额;Q2选择在市场B建立一个服务设施,获得34个单位的市场份额。它们所覆盖的市场总份额为100个单位。
3.(3,1)博弈。假定企业Q1打算在给定的市场环境中建立三个服务设施,只要能够覆盖的消费者个数不少于3RL=60,就满足需求约束。假定企业Q2打算建立一个服务设施,其他条件不变。那么,企业Q1、Q2的收益矩阵如表3所示。很明显,表3所示的博弈没有纳什均衡。
4.(2,2)博弈。假定企业Q1和Q2都打算在给定的市场环境中建立两个服务设施,按照前面的假定,只要这两个设施覆盖的消费者个数不少于2RL=40个单位,平均每个设施能够覆盖的消费者个数不少于RL=20个单位,企业的需求约束就能够得到满足。那么,进行同样的分析可知,对应的博弈也没有纳什均衡。
四、结论
理论上还可用类似的方法分析(3,2)博弈、(3,3)博弈等。但从上述情况已经可以得到一些有意义的结论。
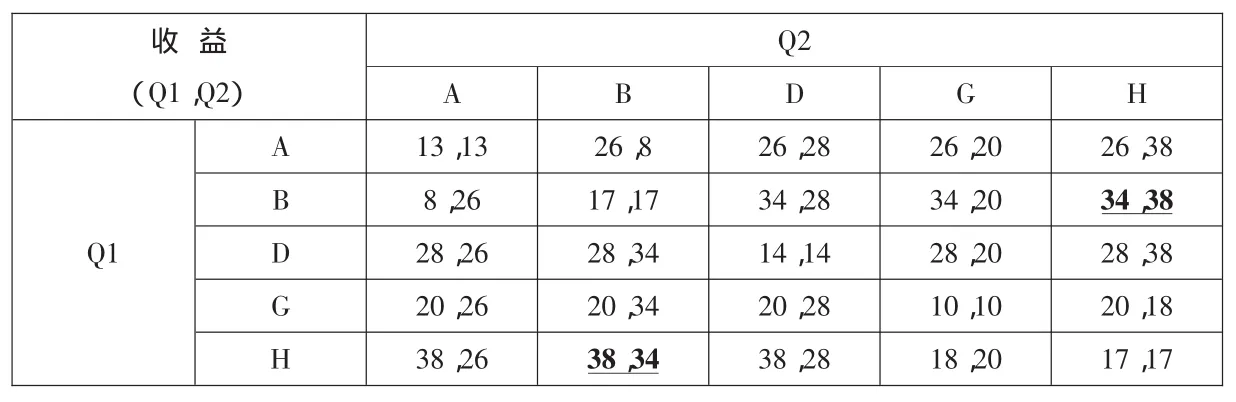
表1 两个企业均建立一个设施的收益矩阵
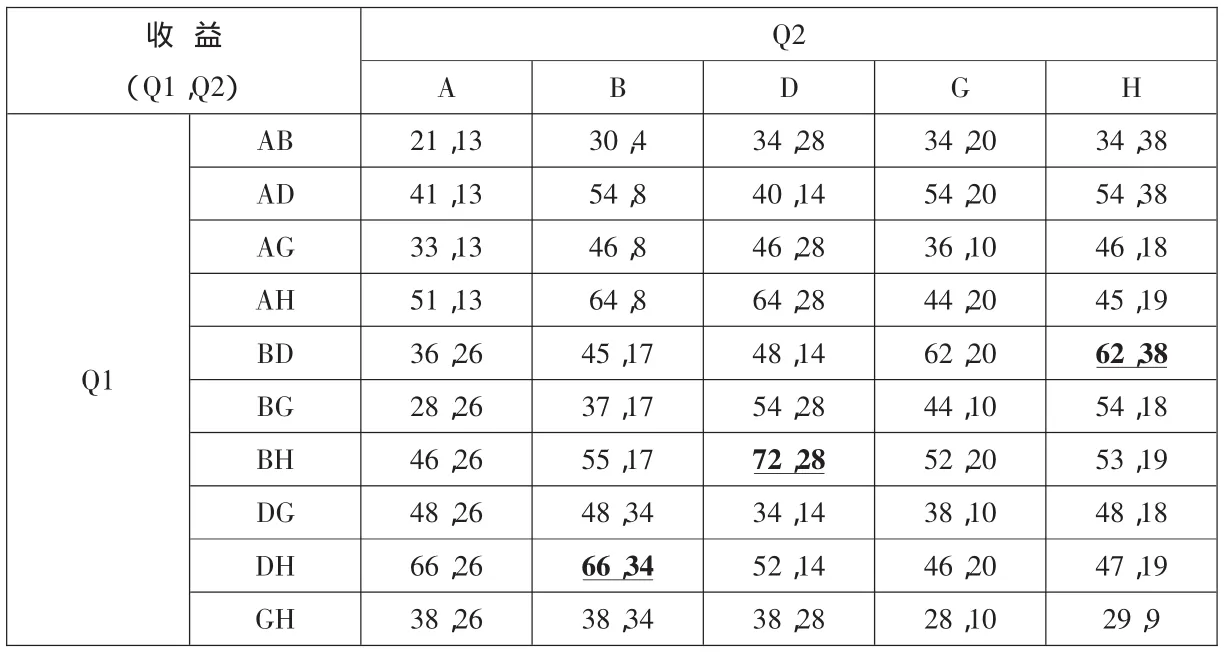
表2 一个企业建立一个设施另一个企业建立两个设施的收益矩阵
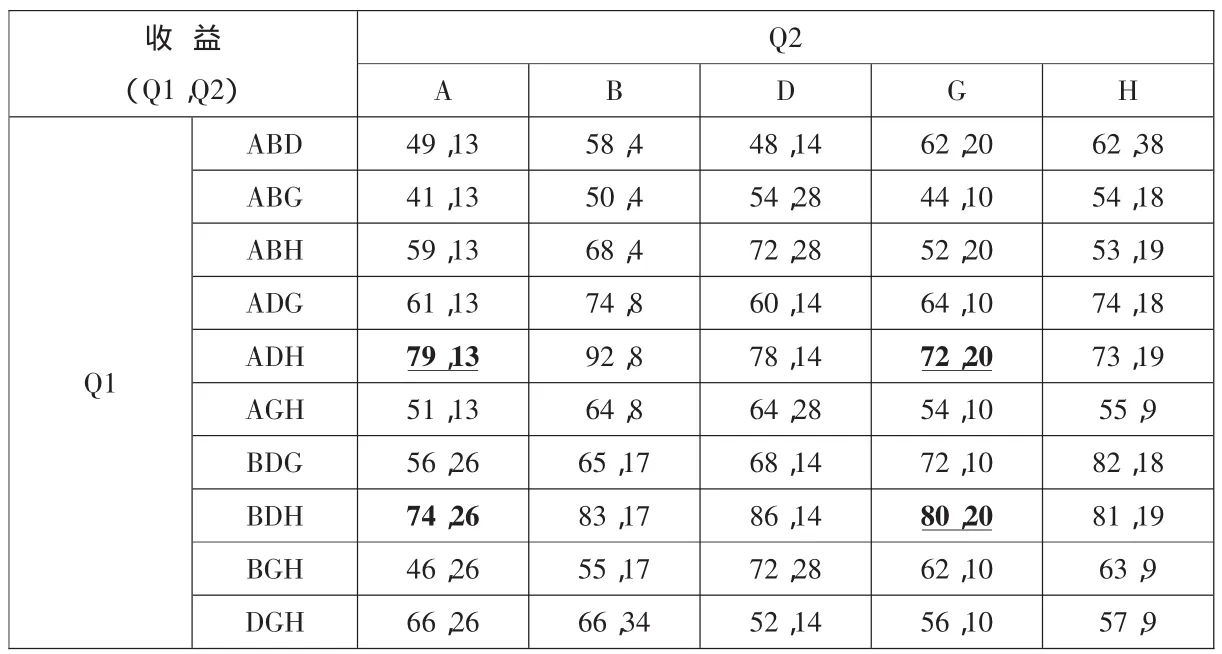
表3 一个企业建立一个设施另一个企业建立三个设施的收益矩阵
1.对于静态选址博弈,不能保证纳什均衡的存在,比如上述的(3,1)博弈和(2,2)博弈。市场环境和企业成本、收益、选址行为都影响均衡的存在,市场的层次嵌套特征在一定程度上会破坏均衡的存在,内层市场较大的市场份额(如B中的A,还有H中的G)吸引着对手的进入,使外层市场均衡受到破坏。
2.在纳什均衡存在的情况下,均衡可以有多个,博弈双方的均衡收益也可以不相等。在(1,1)博弈的情况下,B、H是均衡位置,它们给博弈双方带来的收益分别是38和34。
3.由于成本的约束,服务设施不能保证全社会的需求都得到满足。企业至少能够覆盖20个单位的消费者才会考虑建立设施,市场单位1和(1,1)博弈情况下的市场区域C、D无法覆盖。
4.如果成本不是问题(或者有足够高的利润吸引企业进入),市场覆盖范围可以扩大到一定的程度。但由于利润最大化目标和距离约束的存在,不能保证覆盖全部市场。在(1,1)博弈的情况下,设施建立在B、H,市场区域C、D无法覆盖。但如果能够增加成本多建一个设施,比如在(2,1)博弈情况下增设D,市场区域C、D就能够被覆盖。而对于市场单位1,在现有市场环境下,永远不能覆盖。
*本文系北京市教委“偏覆盖选址模型与算法”(项目编号:KM200810037003)的部分研究成果。
[1]H.Hotelling.Stability in Competition [J].Economic Journal,1929,39:41-57.
[2]S.P.Anderson.Equilibrium Existence in A Linear Model of Spatial Competition[J].Economica,1988,55:479-491.
[3]A.Okabe,M.Aoyagy.Existence of Equilibrium Configurations of Competitive FirmsonAnInfiniteTwo-dimensional Space[J].Journal of Urban Economics,1991,29:349-370.
[4]S.L.Hakimi.LocationwithSpatial Interactions:CompetitiveLocationand Games[A]//R.L.Francis,P.B.Mirchandani(Eds.).Discrete Location Theory[M].New York:Wiley,1990:439-478.
[5]H.A.Eiselt,G.Laporte.Competitive Spatial Models[J].European Journal of Operational Research,1989,39:231-242.
[6]M.Labbe,S.L.Hakimi.Market and Locational Equilibrium for Two Competitors [J].Operations Research,1991,39:749-756.
[7]R.L.Tobin,T.L.Friesz,T.Miller.ExistenceTheoryforSpatiallyCompetitive Network Facility Location Models[J].Annals of Operations Research,1989,18:267-276.
[8]H.A.Eiselt,G.Laporte,J.F.Thisse. Competitive Location Models:A Framework and Bibliography[J].Transportation Science,1993,27:44-54.
[9]H.K.Ahn,S.W.Cheng,O.Cheong,M.Golin,R.Oostrum.Competitive Facility Location:the Voronoi Game[J].Theoretical Computer Science,2004,310:457-467.
[10]V.Mazalov,M.Sakaguchi.Location Game on the Plane[J].International Game Theory Review,2003,5(1):13-25.
[11]A.Ghosh,C.S.Craig.ALocation Allocation Model for Facility Planning in A Competitive Environment[J].Geographical Analysis,1984,16(1):39-51.
[12]W.Christaller.Central Places in Southern Germany[M].New Jersey:Prentice-Hall,1933:58-80.
[13]A.L觟sch.The Economics of Location[M].New Haven:Yale University Press,1940:124-137.
[14]孟尚雄.均衡选址方法研究[J].中国流通经济,2005(9):41-44.
责任编辑:陈静
Abstract:A study about the competitive location by Hotelling in 1929 was on a linear market.Other studies on this subject are on plane,circle,or network markets.This paper addresses the subject on a general market with nested hierarchies.For static models with two firms,it is shown that there is no Nash equilibrium sometimes;even if the equilibria existing,the market shares for two firms may not be equal;the nested hierarchies of markets,to an extent,lead to the non-existence of Nash equilibria because the more shares within inner markets,which motivate the other players in the games to enter,make unstable outer markets;increasing the number of facilities may extend the coverage of marketing areas,but there are some areas which may not be covered under a given marketing environment due to the objectives of profit maximization and the distance constraints on consumers.
Key words:location problems;Nash equilibrium;cluster analysis;nested hierarchies
Location Games for Service Facilities
MENGShang-xiong
(Beijing Wuzi University,Beijing101149,China)
F061.5
A
1007-8266(2010)09-0049-04
孟尚雄(1963-),男,山西省代县人,北京物资学院经济学院副教授,首都经济贸易大学统计学院博士生,主要研究方向为空间统计、空间经济和选址理论。

