基于 CART决策树的复杂生产过程质量预测方法研究*

戚长松,余忠华,侯智,杨振生

(浙江大学现代制造工程研究所,杭州 310027)

0 引言

由于复杂生产过程具有工艺参数众多、机理复杂、非线性显著和动态变化等特点,难以用常规方法建立其精确的数学模型[1]。同时,随着工业自动化技术和计算机信息技术的快速发展及应用,在生产现场又积累了海量的数据,激发了人们对分析这些数据的浓厚兴趣,以识别和发掘其中隐藏的规律,更好地指导生产实践。

统计质量控制方法关注于生产工序的质量波动性,通过统计推断预测工序的变异性,以便及时展开工艺调整。模糊分类法[2]、人工神经网络[3-5]、贝叶斯分类法[6]和支持向量机[7]等数据挖掘方法可以对工序质量进行分析和预测,取得了较好的应用效果。相比之下,决策树(Decision Tree)方法具有易于处理变化的数据、对噪声数据具有健壮性、生产规则容易理解、识别效率高等优点,决策树中的 CART(CART：Classification And Regression Tree)算法可以使用回归方程的形式进行预测变量建模,因此该方法非常适用于具有以上特性的复杂生产过程质量预测研究。

本文针对复杂生产过程,面向决策树应用构建生产过程信息模型,并以陶瓷管生产过程为例,运用 CART决策树算法进行了快速、有效的生产过程质量预测。

1 复杂生产过程 CART决策树构建

CART决策树法是由 Breiman等人于 1984年提出的决策树构建算法[8-10]。同其它决策树算法如 ID3和CHAID相比较,CART算法的最大特点在于它可以处理目标变量是连续型变量的情形。该方法使用替代变量(Surrogate Variable)[11]可有效解决分析中出现缺失数据的问题。同时,它不要求预测变量与目标变量之间具有某种特定的分布,还能有效地处理非线性问题的建模与求解。因此,非常适合于解决复杂生产过程的质量预测问题。

图 1为本文给出的一种面向复杂生产过程质量预测的 CART决策树构建模型。其主要步骤包括：①识别复杂生产过程中产品关键质量特性(Y)及其相关的工艺特性参数(X),构成一组参数集{Y：X},进而形成决策树模型的训练集;②利用 CART生长算法,建立CART决策树;③依据剪枝算法对训练集进行机器学习,得到一系列决策树模型;④使用交叉验证法(Cross-Validation)进行模型评估,得到可以用于质量预测的最优决策树模型。⑤最后,利用所建立的最优决策树模型,对生产过程进行质量预测,以指导工艺调整。

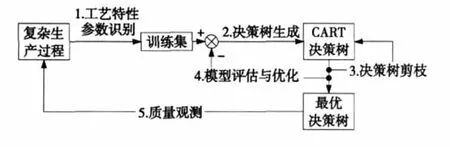
图 1 复杂生产过程CART决策树模型构建过程图

1.1 工艺特性参数识别

复杂生产过程中评定产品质量的特性指标往往有多个,而影响这些指标的工艺因素则更多。进行质量预测研究需要有选择性地识别其工艺特性参数,构成一组由产品关键质量特性 Y={Y1,Y2,…,Yn}及其工艺特性参数 X={X1,X2,…,Xn}所组成的参数集{Y：X},并采集足够的训练样本。这一环节是构建决策树预测模型的基础与前提,直接关系到模型预测的准确性,通常需结合实际案例采用因果图、排列图等辅助工具及专家评定的方法来解决。

这里,以氧化铝陶瓷管生产过程为例进行说明,该生产过程包括：原料采购、混料、球磨、喷雾造粒、成型、素烧、烧结等关键工序,如图 2所示。通过对现场的分析及专家的经验,选取松装密度(Y1)、流动性(Y2)、含水率(Y3)作为产品关键质量特性 Y={Y1,Y2,Y3};其工艺特性参数 X则包括：球磨工序的球磨机型号(X1)和料浆粘度(以球磨后料浆过筛目数度量)(X2),喷雾造粒工序的喷嘴口径(X3)、喷雾压力(X4)、入口温度(X5)和出口温度(X6),即 X={X1,X2,…,X6}。以上关键质量特性 Y={Y1,Y2,Y3}和工艺特性参数 X={X1,X2,…,X6}将用于 CART决策树的生成和剪枝。

图 2 陶瓷管主要工艺路线图

1.2 CART决策树的生成

决策树生长算法的关键在于从可用的属性中选择每个节点的分裂属性,使得决策树的分类精度达到最高。树的生长过程实际就是不断的把数据集进行分割的过程,每次分割对应于一个节点中的一个问题,对每个分割都要求分到同一分枝中的数据记录间的“差异”最小(即属于同一个类),而不同分枝间的数据记录的“差异”最大(即属于不同的类)。度量这个“差异”的指标称之为不纯性,这样便可用不纯性度量指标来控制 CART模型的分割行为。

一般,在数据分类时,常用 Gini指数度量节点的不纯性。即,节点 t的 Gini指数 GINI(t)定义为：

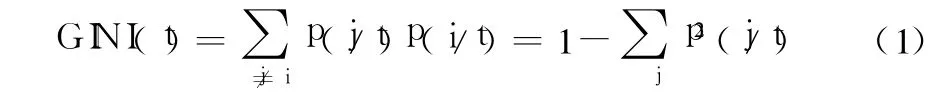
其中,i和 j是目标变量的类别,p(j/t),p(j/t)表示目标类别 i,j在节点 t中出现的比例。假定节点 t的下一代子节点分为 tL和tR,则不纯度指标的下降量表示为式(2)：

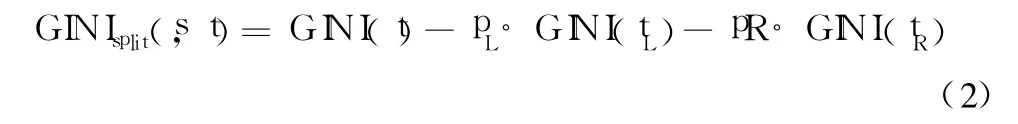
其中,pL是 t中送到左边子女节点的实例所占的比例,pR是 t中送到右边子女节点的实例所占的比例。s∈ S是所有可能的分割集 S中的一个具体分割。CART的生长就是选择分割s,最大化GINIsplit(s,t)的值。由于对于节点 t上的任意分割 s,GINI(t)是常量,因此,问题就变为选择分割 s,使得式(3)中的 Gain(s,t)最小。

CART用于数据预测时,任何一次分割通过式(4)计算节点 N包含样本的响应变量 y的冗余平方和D(μ,y)：

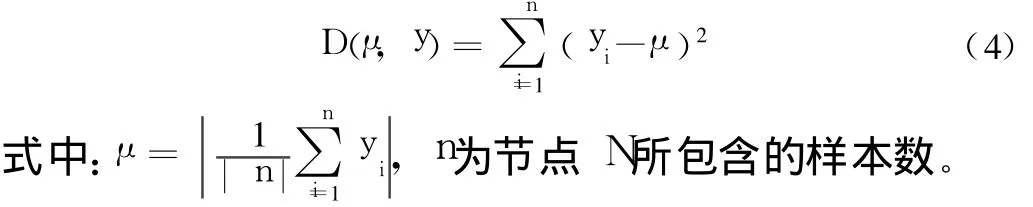
同样分别计算左右节点的冗余平方和,选择使得当前节点 N的冗余平方和与左右节点冗余平方和之差最大的查询作为分割规则。

1.3 CART决策树的剪枝

使用递归分割训练集而得到的决策树随着树的生长,最佳分割的选择所依据的样本将越来越小,这就意味着随着树的生长,其估计结果变得越来越不可靠。当训练集数据存在噪声的情况下,生成的决策树将与训练实例完全拟合,也称过度拟合(overfitting),这种情况下一些噪声和干扰数据也被包括进来,即决策树捕获了训练样本的规律,而不是得到了样本领域(总体)的规律,亦即对训练数据的完全拟合反而不具有很好的预测性能。

剪枝是一种克服噪声的技术,通过剪枝算法可以将决策树的准确率提高达 25%[12],同时它也能使树得到简化而变得更容易理解。CART算法采用交叉验证法进行修剪,最终分析结果是一棵兼顾复杂度和错误率的最优二叉树[8,13]。选择最优的剪枝树即是选择最优的复杂度参数 α[14]使得式(5)值最小,当样本数目不大时,往往希望用全部的数据来构建树,采用交叉有效性评估方法使每一个样本既用于构建树,同时用于估计冗余平方和,进而确定 α实现最优树的选择。

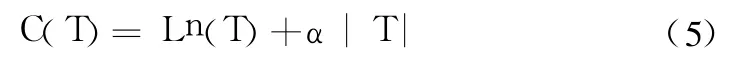
式中：C(T)表示该树的加权错分率与复杂度处罚值之和的复合成本;|T|表示过度训练树叶节点的数目;α为复杂度参数,如果 α足够大,则得到一个只有根节点的决策树树;对于 0=α1＜α2＜… ＜αk,整数k≤|T|,因此可以生成节点数逐次降低的 CART序列 fα1,…,fαk,其中 fα1为初始未经剪枝的树 ,fαk为仅包含根节点的树。将 CART作为预测模型时定义式(6)中：

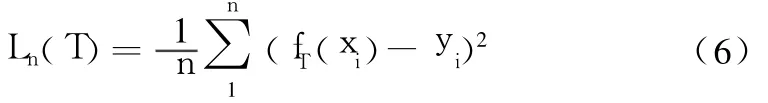
作为分类模型时定义式(7)中：

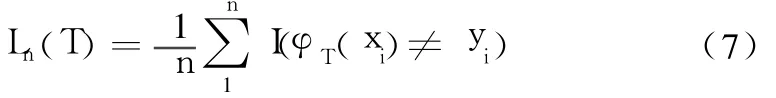
式中：I为隐含函数关系。

1.4 模型的评估与优化

为了在样本数目有限的情况下,更有效地评估模型的准确性,将使用交叉验证法(Cross-Validation)进行模型评估。交叉验证法对于样本数据相对少的问题具有很强的适用性。该法中所有样本被划分成 k个互不相交的子集 S1,S2,…,Sk,每个子集的样本数目大致相等。图 1所示的子过程(步骤 2-步骤 3-步骤 4)进行 k次循环。第 i次中 Si作为测试数据集,其余子集都用作训练数据集。首先,使用训练数据集生成初始决策树模型;其次,利用最小代价复杂性剪枝算法对初始决策树进行剪枝,从而得到具有不同复杂度参数 α的决策树;最后,使用测试数据集来评估模型的预测准确率,结合模型复杂度和准确性的评估,确定可以进行质量预测的决策树模型。

最终得到的决策树的层数不宜过多或过少。如果层次过多,则表示分割过多,所产生的规则也会因为过于细致而失去分类效力;相反,如果层次太少,即表示分割过程太早,所建模型未必产生良好的分类规则。

2 应用实例

针对陶瓷管生产过程,按照以上模型构建过程建立用于质量预测的 CART决策树模型。决策树建模工具选择 Spss Clementine 11数据挖掘平台,以目标变量为流动性(Y2)为例进行应用实例研究。

工艺特性参数识别阶段,选取工艺特性参数 X作为预测变量,选取产品关键质量特性 Y作为目标变量,训练集样本取自某公司生产现场的测试结果,共采集了 486条数据,部分数据如表 1所示。

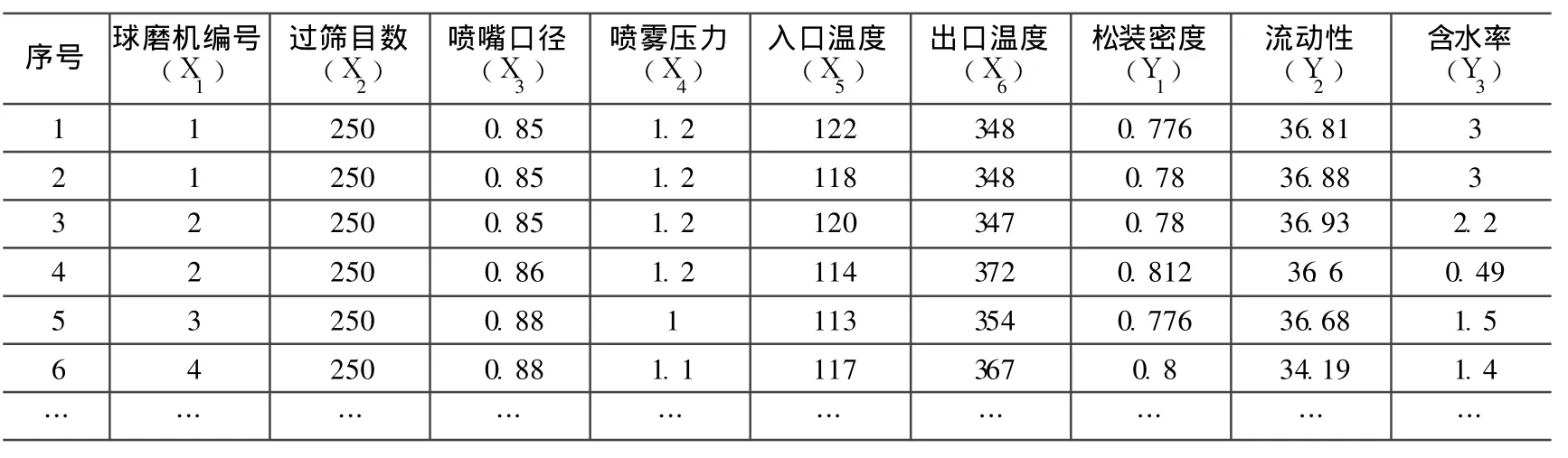
表 1 用于决策树建模的数据集结构和样本表

决策树生成阶段,最大树状图深度设置为 5;控制树生长的最小杂质改变设置为 0.003,即如果某个分支的最佳分割按小于指定值的数量减少杂质,则不会进行此分割,如果不进行剪枝则获得最大决策树如图 3a所示。

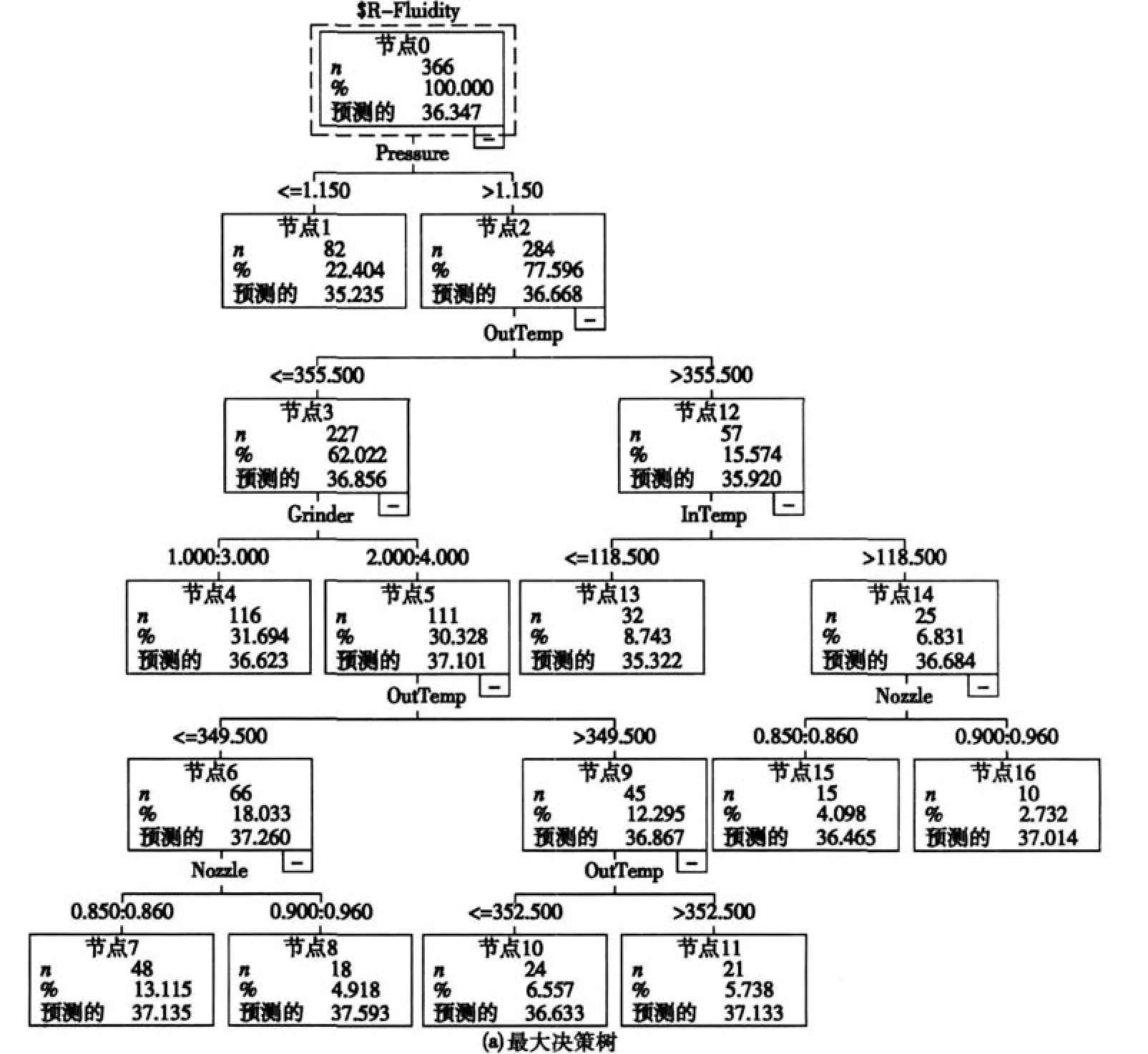
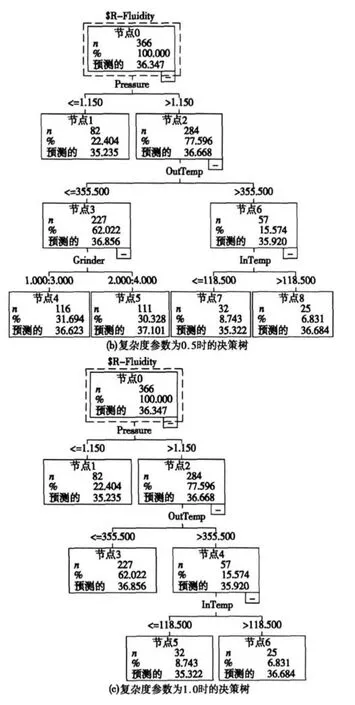
图 3 陶瓷管生产过程决策树(以目标变量为流动性为例)

决策树剪枝阶段,为避免过度拟合,式(5)中的复杂度参数 α设置为 0.5和 1,获得剪枝后的决策树如图3b和图 3c所示。

下面对以上三个模型的准确率进行评估,结果见表 2。其中当复杂度参数 α=1时,决策树具有最简单的形式,但是平均预测误差为 2.64%,均方误差为2.44%,两个指标都偏大;当不进行剪枝时,平均预测误差为 2.54%,三者中最小,但是如图 3a所示的决策树模型及其规则过于复杂,预测效率不高;当复杂度参数 α=0.5时,预测的均方误差为 2.41%,是三者中最小,且平均预测误差为 2.62%,小于当复杂度参数α=1时的平均预测误差 2.64%,同时如图 3b所示的决策树模型相对于图 3a所示的模型要简化很多,即达到了复杂度和错误率的平衡。综上所述,选择复杂度参数 α=0.5时的决策树模型,图3b所示,作为流动性的预测模型。

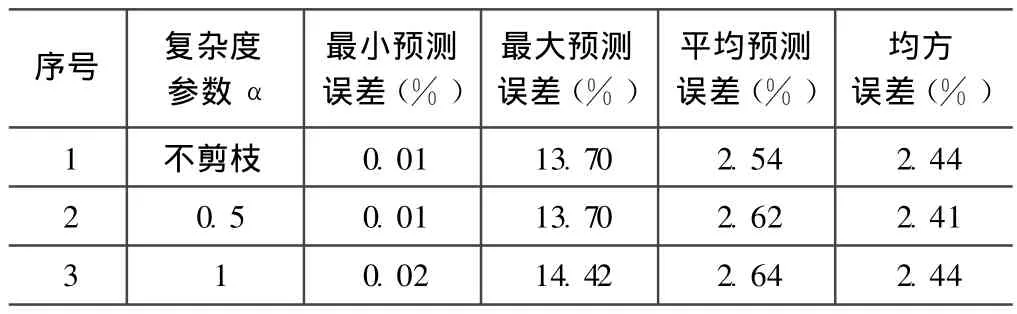
表 2 复杂度参数α不同时模型准确性评估结果

图 3b所示的决策模型共有 5个叶节点,每个叶节点对应一条规则,共 5条规则,每个节点对应的规则如下：

其中,Pressure代表喷雾压力(X4);OutTemp代表出口温度(X6);Grinder代表球磨机编号(X1);InTemp代表入口温度(X5)。“=＞”之后的数值表示流动性的预测值,预测值后面括号里面的数字代表支持该规则的样本个数。

由于树的建立过程是一个不断选择最佳预测变量的过程,因此在划分数据方面,高层结点上的分类规则比低层结点上的分类规则更有价值,所以可以根据分类规则在分类树的位置确定预测变量对目标变量的影响的重要性,从图 3b所示的决策树模型中可以看出针对流动性这一目标变量,预测变量的重要性排序为：喷雾压力(X4)＞出口温度(X6)＞球磨机编号(X1)和入口温度(X5)。

3 结束语

针对复杂生产过程质量影响因素分布范围广、时间跨度大的特点,构建基于 CART决策树的质量预测模型,用一系列过程预测变量的逻辑表达式构成陶瓷管生产质量分类、预测的规则,并对预测变量的重要度进行排序。该模型能够有效地处理复杂生产过程的海量质量数据。使得一个复杂的参数优化与决策过程的时间显著减少,效率大大提高。CART测试结果表明,基于 CART算法的决策树可以较为满意地完成陶瓷管生产过程的质量预测工作。

[1]古钟璧,王祯学,胡丽莉.复杂生产过程的模糊神经网络辨识[J].四川大学学报(自然科学版),1997(6)：801-806.

[2]吴敏,徐辰华,王春生.基于模糊分类变系数的铅锌烧结过程综合透气性状态预测[J].华东理工大学学报(自然科学版),2006(7)：19-23.

[3]王伟,娄相芽,杨永红,等.基于 RBF人工神经网络的喷丸成形工艺参数预测方法[J].组合机床与自动化加工技术,2008(8)：43-45,49.

[4]黄松林,崔建忠.基于人工神经网络的铝合金铸锭裂纹倾向预测[J].中国有色金属学报,2008(9)：1699-1705.

[5]贾剑平,徐坤刚,李志刚.改进型 BP网络在优化焊接工艺参数中的应用[J].热加工工艺,2008(21)：98-100.

[6]龚淑华,刘祥官.模糊贝叶斯网络应用于预测高炉铁水含硅量变化趋势[J].冶金自动化,2005(5)：30-32,42.

[7]董华,杨世元,吴德会.基于模糊支持向量机的小批量生产质量智能预测方法[J].系统工程理论与实践,2007(3)：98-104.

[8]Breiman L,Friedman J,Olshen R.Classification and regression trees[M].California：Wadsworth Belement,1984.

[9]Scott CD,Willett RM,Nowak R D.Classification or regression Trees[J].IEEE Acoustics Speech and Signal Processing,2003,4(6)：153-156.

[10]Bittencourt H R,Clarke R T.Use of classification and regression trees(CART)to classify remotely-sensed digital images[J].IEEE Geoscience and Remote Sensing Symposium,2003,7(6)：3751-3753.

[11]Chebrolu,Srilatha,Abraham.Feature deduction and ensemble design of intrusion detection systems[J].Computers and Security,2005,24(4)：295-307.

[12]J.Mingers,An empirical comparison of pruningmethods for decision tree induction[J].Machine Learning,1989(4)：227-243.

[13]Yohannes Y,Hoddinott J.Classification and Regression Tree：An Introduction[M].Washington,D.C.,U.S.A.：International Food Policy Research Institute,1999.

[14]F Esposito,D Malerba,G Semeraro.A com parative analysis ofmethods for pruning decision trees[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(5)：476-491.