基于神经网络的电火花线切割加工工艺仿真研究

张利堂,刘勇,杜树浩

(西华大学机械工程与自动化学院,成都 610039)

0 引言

电火花线切割加工技术(WEDM)作为一种与机械加工性质完全不同的技术,已被广泛应用于精密冲模、粉末冶金压模、样板、成形刀具及特殊零件加工等领域[1]。但其加工过程是一个包含多参数的复杂过程,具有随机性和不确定性[2]。在实际应用中,电火花线切割加工所选取的工艺参数直接决定工艺效果,而工艺参数的选取往往取决于操作人员的经验和技术水平。由于其机理比较复杂,影响因素较多,故仅凭操作人员的经验,主观地选择工艺参数进行加工,往往不能充分地发挥机床的性能,从而影响加工工艺效果。而解决工艺参数选择难的关键是建立一个合理有效的电火花线切割加工模型,并应用此模型实现在全局范围内加工效果的预测,进而指导实际生产。

1 电火花加工工艺试验设计

1.1 试验条件

机床：江苏方正数控机床厂生产的 DK3320

电源输出电压： 75V

电极丝规格为： 钼丝(0.13mm)

电极丝进给速度：10m/s

工作液： 皂化油

工件材料： 45#钢

1.2 试验方案拟订[3]

本文结合实际情况,选用了二次通用旋转组合设计。具体就是使到试验中心点距离相等的球面上,各点回归方程预测的方差相等。由于在此方法设计中,预测值的方差仅与试验点到试验中心点的距离有关,而与方向无关。所以可以消除寻找最佳工艺过程中的误差干扰。再者此设计方法试验次数少,计算简便,并且又克服了以往设计方法依赖试验点在因子空间中位置的缺点。故此选择二次通用旋转组合设计,其试验次数确定公式为：

式中：MC其值为 2p,是两水平(+1,-1)的全因子试验点个数;2P表示在P个坐标轴上的星号点,它们与中心点的距离 γ称为星号臂,其中 γ是待定参数;M0表示在各变量都取零水平的中心点的重复试验次数,一般取(3-8)。

二次通用旋转组合设计试验的具体参数和试验次数如表 1所示。

表 1 试验参数和次数的设计

通过试验获取 32组数据,其中 24组作为拟合数据,8组作为预测数据。

2 加工工艺仿真及预测

2.1 传统工艺仿真[2-3]

传统工艺建模方法是采用多项式曲线拟合,研究变量与目标变量之间的关系。

具体以工件厚度(mm)、平均间隙电流(A)、脉冲宽度(μs)、脉冲间隔(μs)为变量,且分别定义为 x1、x2、x3、x4;取加工速度 (mm2/min)、表面粗糙度 (μm)为目标变量。

2.1.1 加工速度 V的曲线拟合

选取加工速度 V的拟合曲线为：

该曲线不是通过所有试验数据点(x1i,x2i,x3i,x4i,Vi),而是参差平方和最小,即使式(3)为最小的曲线：

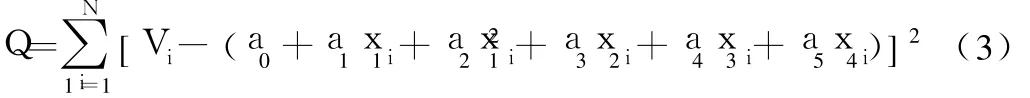
要求解出aj(j=0,1,2,3,4,5)的方法就是使Q达到极限的参数 aj(j=0,1,2,3,4,5)应满足 ∂Q/∂aj=0即满足下式(4)：

这是关于 aj(j=0,1,2,3,4,5)的线性方程组,通常称为正则方程组,有唯一解,整理后,带入试验数据解之：

拟合曲线为：

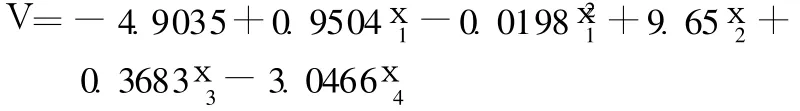
同理可得粗糙度拟合曲线为：

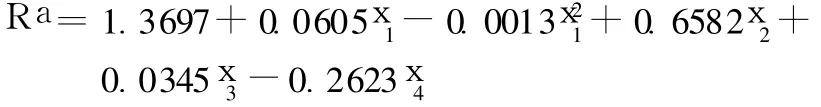
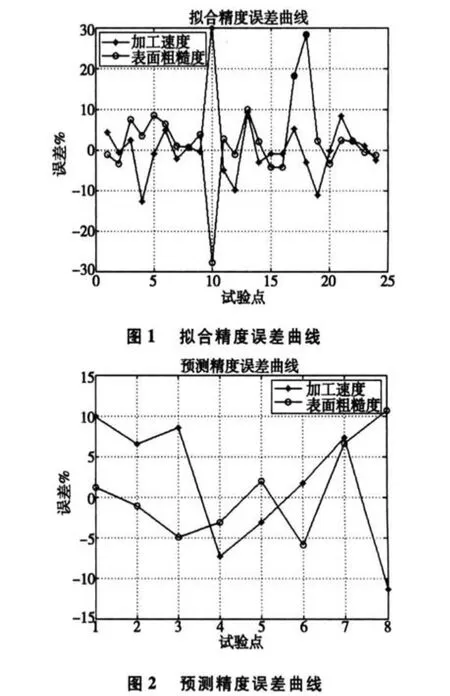
其中图 1和图 2分别为传统建模得到的数据与试验拟合、预测数据对比的精度误差曲线图。

2.1.2 小结

从上述可看出：拟合的加工速度和表面粗糙度的相对误差最大分别为 29.92%、-27.83%;预测的加工速度和表面粗糙度的相对误差最大分别为 -11.32%、10.69%;拟合、预测的加工速度和表面粗糙度各自的相对平均误差分别为 7.57%、5.12%、6.99%、4.46%。因此,明显看出传统工艺仿真的建模极其繁琐、分析和计算工作量大、拟合预测精度低,不但浪费人力、物力,还不能有效的保证精度,对实际的指导意义不大。

2.2 基于 RBF神经网络工艺仿真

2.2.1 概述

人工神经网络是借鉴于生物神经网络而发展起来的智能信息处理系统,是由大量神经元交互连接而组成的并行非线性系统,具有自学习、自组织、自适应性以及良好的容错性等特点,对输入的采样数据可实现分类识别、优化计算、处理知识的能力,尤其对那些复杂的非线性问题,可利用人工神经网络作为一种建模的新型工具。电火花线切割的高度非线性,恰好为展现神经网络的优越性提供了平台。目前最常用的 BP网络,虽然具有反向传播功能,但其对样本的学习效率低、收敛速度慢,又容易形成局部极小等缺点,而 RBF网络作为另一类常用的前馈网络,也可以用于函数逼近与分类。与其相比不但具有生理学基础,而且结构更简洁,学习速度也更快[4]。故此选用RBF网络来构造电火花线切割工艺参数模型,以建立工艺效果的仿真系统。

2.2.2 神经网络模拟结构、隐含层神经元数量确定

典型的神经网络结构由三个部分组成：输入层、隐含层和输出层。这三部分之间通过各层节点之间的连接权依次前向连接。一个三层的 RBF神经网络可完成任意 N维(输入变量维数)到 M维(输出变量维数)的映射。用这三层神经网络可对应表示输入输出的映射能力,以及模拟线切割实际加工过程中输入输出之间的复杂函数关系。初步拟定输入层为：平均间隙电流(A);脉冲宽度 (μs);脉冲间隔;工件厚度(mm)。输出层为：加工速度(mm2/min);表面粗糙度(Ra)。RBF网络模拟结构如图 3所示。

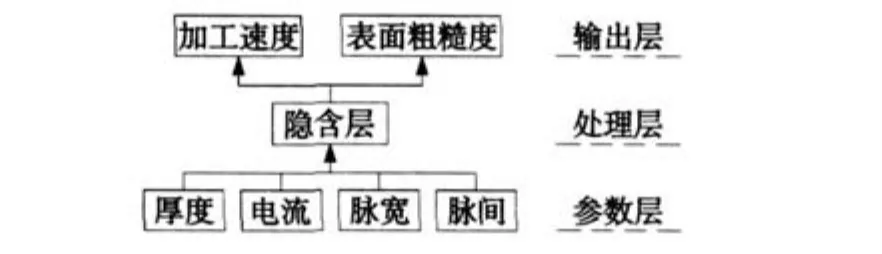
图 3 RBF网络模拟结构图

隐含层神经元数量传统的确定做法是使其与输入向量的元素相等。显然,在输入矢量很多时,过多的隐含层单元数是难以让人接受的。为此,有了新的改进方法,基本原理是：从 0个神经元开始训练,通过检查输出误差使网络自动增加神经元。每次循环使用,使网络产生的最大误差所对应的输入向量作为权值向量 w1,产生一个新的隐含层神经元,然后检查新网络的误差,重复此过程直到达到误差要求或最大隐含层神经元数为止[5]。

2.2.3 RBF神经网络算法[5-6]

RBF网络中,径向基函数都是对称的,常用的是高斯函数,可表示为：

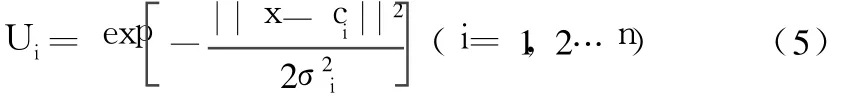
式中,n为输出层的节点数。

输入层实现从x→Ui(x)的非线性映射,输出层实现从 Ui(x)→yk的线性映射,即：

RBF的网络训练方法可表示为：初始化,根据所有输入样本来确定隐含层节点的高斯函数的参数(中心值 ci和标准常数 σi)初值。随后用聚类分析中的 K-NN算法求取网络高斯函数的参数,最后依据输入样本,利用系统辩识理论中的最小二乘算法求出层的权值。其中隐含层和输出层之间的连接权的学习算法为：

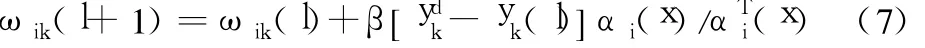
2.2.4 RBF神经网络的 MATLAB实现[7-9]

Matlab神经网络工具箱提供了许多经典的学习算法,由于其编程简单,使得使用者节省了大量的时间,更有精力投入到网络的设计上。因此根据上述算法,以Matlab为平台,首先调用里面的函数 premnmx对试验数据进行归一化处理。随后用函数 newrb()来创建一个径向基神经网络,它是RBF网络的一种变换形式,特点是训练速度快,非线性映射能力强。具体调用格式为：

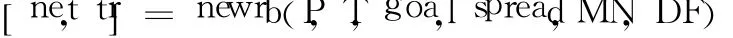
式中,P代表输入矢量,T代表目标矢量,goal为均方误差性能指标,默认为 0;spread为径向基函数的分布密度,默认值为 1;MN为神经元个数最大值,缺省值为输入矢量的个数;DF为训练过程的显示频率,缺省值为 25。理论上讲,spread越小,对函数的逼近就越精确,但是逼近的过程就越不平滑;spread越大,逼近过程就比较平滑,但是逼近误差会比较大。

径向基网络设计训练好以后便可对网络进行仿真。其调用格式为：

上述 RBF网络训练仿真的部分 MATLAB代码为：

对数据进行归一化处理后,采用上述的网络创建函数即可对网络进行训练,也就是建模过程。其训练过程如图 4所示,网络的目标误差为 0.001,网络的神经元个数为 22个。绘制拟合、预测图分别如图 5、图 6所示。

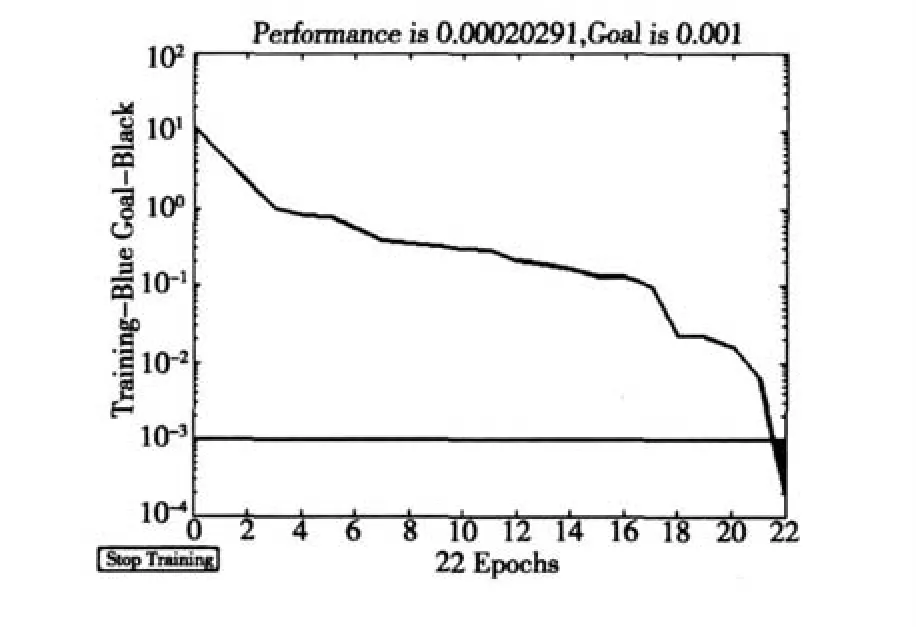
图 4 训练误差曲线

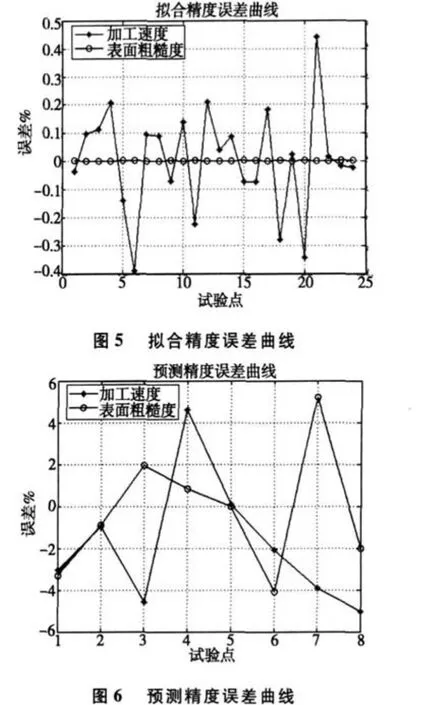
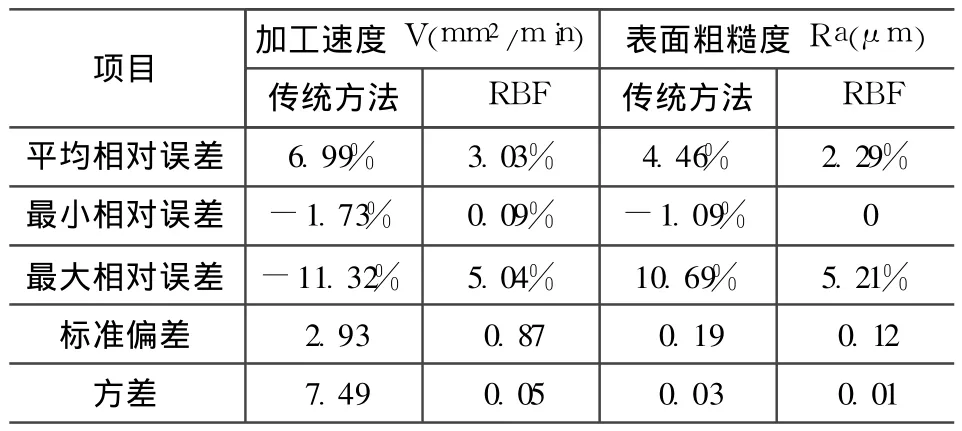
表 2 传统方法和RBF网络的预测精度效果

从上图 5、图 6以及表 2可以看出：RBF网络的拟合精度和预测精度都比较理想,特别是表面粗糙度的拟合误差为 0,切割速度和表面粗糙度的相对平均预测误差分别为 3.03%和 2.29%;而传统的相对平均预测误差则分别为 6.99%和 4.46%。显而易见基于 RBF神经网络模型在拟合、预测各方面指标均优于采用传统的多项式曲线拟合模型,与实际情况十分接近,这就是 RBF网络的优势体现。因此建立基于 RBF神经网络的线切割加工工艺的仿真具有良好的工艺效果。

2.2.5 仿真的模块化[7,10]

再以 MATLAB为平台,利用内部函数 gensim()能对一个神经网络生产模块化描述,从而可在 simulink中对其进行仿真。gensim()函数的调用格式为：

式中,第一个参数指定了 MATALB工作空间中需要生成模块化描述的网络,第二个参数指定了采样时间,通常情况下为一正数。如果网络没有与输入权值或层中权值相关的延迟,则指定第二个参数为 -1,那么函数gensim()将生成一个连续采样的网络。其仿真模块为图 7所示。

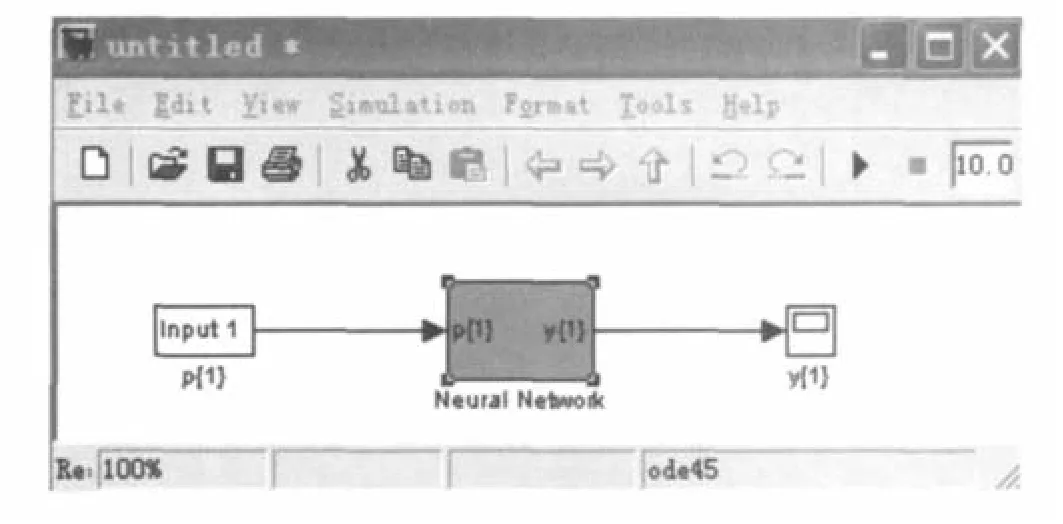
图 7 RBF网络的仿真图

图中 RBF网络 net使用一个神经网络模块来代替。双击此模块,将弹出一个新的窗口,绘出了此网络的结构,该网络包含两层,这个结构还不够具体,不能满足要求,还可以进一步在其基础上双击需要了解的部分。以此类推,便可查看 Layer1、Layer2的结构,及其权值 weight的调整结构,分别如图 8、图 9所示。

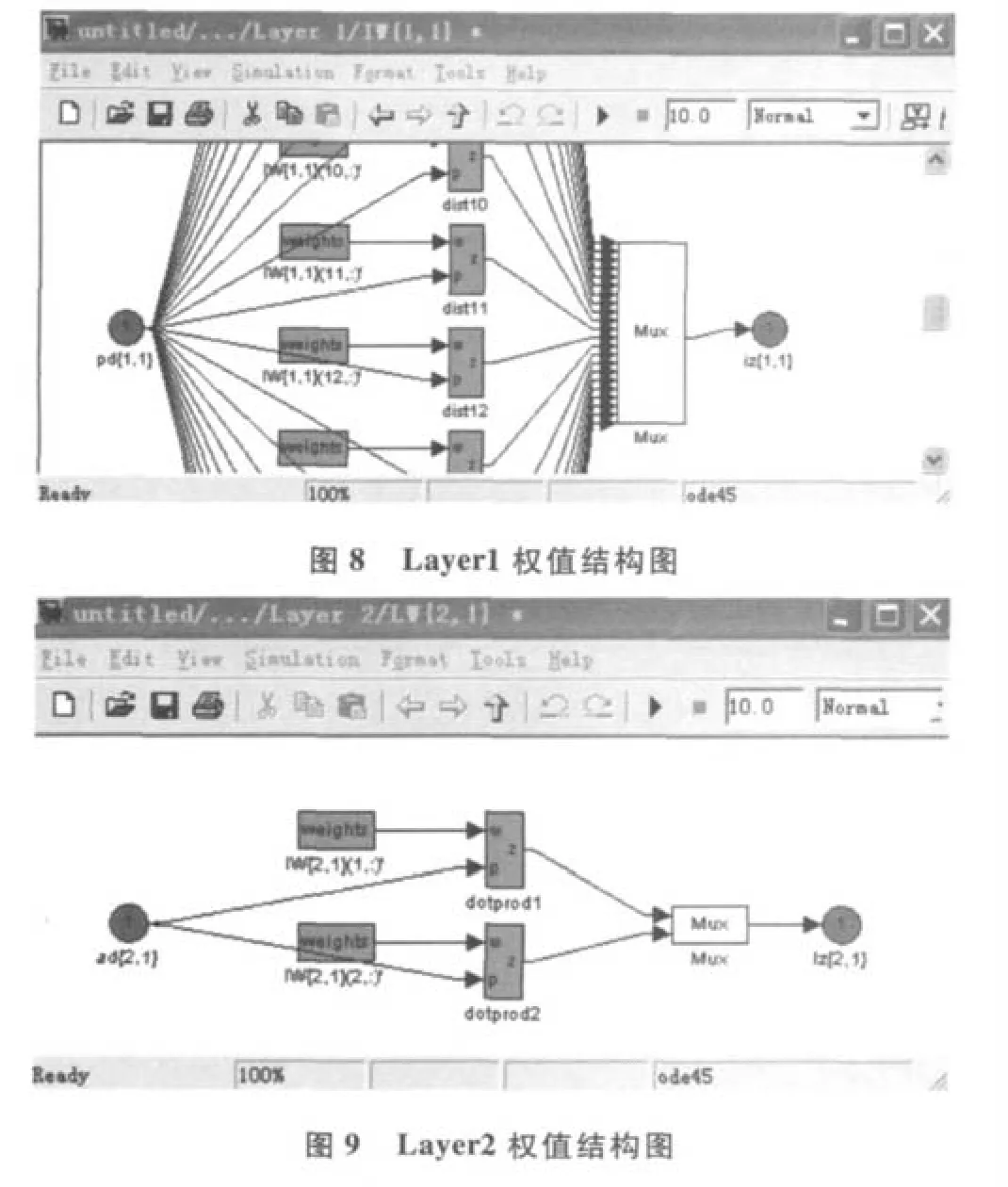
RBF网络模块化以后,只需在 input1中输入加工参数,然后运行该仿真系统,就可在示波器中查看拟合或者预测的结果,而且简单明了,因此仿真的效率获得了较大的提高。

3 结束语

(1)利用神经网络技术建立了电火花线切割加工工艺模型,通过试验对比发现神经网络建模优于传统方法建模,其避免了繁杂的分析和计算,具有较高的精度,并且试验表明神经网络建模预测误差基本控制在6%以内,体现了其收敛速度和预测精度的优越性,为实现以后工艺参数的优化选择奠定了基础。

(2)该建模方法使用范围广,只要其他的电火花机床具有相应的工艺样本,再通过神经网络的学习,进一步完善训练样本,不但针对该机床可建立加工工艺模型,而且可以使预测精度得到进一步的提高。

(3)以 MATLAB为平台的网络模块化实现,是对仿真的升华。其具有三大功能：工艺过程仿真、效果的预测以及加工参数的优化选取。在一定程度上减少了工作量,降低了工作强度,提高了仿真的效率,对以后实际生产的指导具有重要意义。

[1]曹凤国.电火花加工技术[M].北京：化学工业出版社,2004.

[2]王晓亚.高速走丝线切割工艺建模方法及仿真系统的研究[D].浙江：浙江大学,2003.

[3]任露泉.试验优化技术与分析[M].北京：高等教育出版社,2003.

[4]魏海坤.神经网络结构设计的理论与方法[M].北京：国防工业出版社,2005.

[5]田景文.人工神经网络算法研究及应用[M].北京：北京理工大学出版社,2006.

[6]楼月明,李明辉,彭颖红.利用神经网络建立电火花加工工艺模型[J].中国机械工程,2001(4)：408-410.

[7]许东,吴铮.基于 MATLAB 6.x的系统分析与设计——神经网络[M].西安：西安电子科技大学出版社,2003.

[8]葛哲学,孙志强.神经网络理论与 MATLAB R 2007实现[M].北京：电子工业出版社,2007.

[9]周开利,康耀红.神经网络模型及其 MATLAB仿真程序设计[M].北京：清华大学出版社,2005.

[10]董长虹.MATLAB应用丛书——神经网络与应用[M].北京：国防工业出版社,2005.