计算电力系统电压分叉点的新方法

井雨刚，李英秋

（1.山东电力研究院，山东 济南 250002；2.山东达驰电气有限公司，山东 济南 250002）

计算电力系统电压分叉点的新方法

井雨刚1，李英秋2

（1.山东电力研究院，山东 济南 250002；2.山东达驰电气有限公司，山东 济南 250002）

基于电力系统动态模型，应用分叉理论提出了一种求解鞍结分叉、hopf分叉点的新方法。该方法的基本原理是，当动态系统参数缓慢变化时，在其平衡点的延拓过程中，首先检测该平衡点流形的局部领域内系统的拓扑性质的改变，确定系统动态稳定性性态，然后应用插值法来确定更高精度要求的参数分叉值，典型电压稳定模型的计算结果表明了此方法的有效性和实用性。

鞍结分叉；hopf分叉；仿连续法；动态电压稳定

0 引言

电力系统是一个高度非线性的动态系统，电压稳定性的研究是现代电力系统稳定分析中的一个重要组成部分，必然具有非线性的特征，因此应用非线性方法进行机理分析和防范措施的设计是很自然的。分叉理论作为分析非线性动力系统稳定性的基本方法，已经在电力系统电压稳定问题中得到了广泛的应用［1~6］。在电力系统中，所发现的分叉类型主要有鞍结点分叉（saddle-node bifurcation，缩写为SNB）、霍普夫分叉（Hopf bifurcation）等。

目前，鞍结分叉点与系统电压崩溃点的对应关系已经为大多数人所接受，常规电力系统电压静稳定性也正是以运行点与鞍结分叉点之间的距离来衡量。文献［7］也较早指出鞍结分叉的灾变性后果是电压崩溃的内在原因。然而以往发生的一些事故经验表明：在系统发生电压崩溃前或崩溃的过程中，常会经历电压振荡现象。这说明由于一些原因，系统在抵达鞍结分叉点之前会首先遇到动态分叉点。文献［8］针对文献［7］的模型，指出该系统也将发生Hopf分叉，且随着负荷参数的进一步变化，系统将出现称为blue-sky的灾变现象，因此系统出现Hopf分叉也将是电压失稳的开端。

目前寻找流形上分叉点的方法可以归结为2类：①计算出所有随控制参数变化的系统雅可比矩阵特征值，进而判断是否有特征值穿越特征复平面的虚轴，以确定分叉点；②根据经典Hurwitz行列式符号变化，搜索判断分叉点。很明显，第一种方法由于要计算系统雅可比矩阵所有特征值，计算量大；而第二种方法对于高维情形，构造出特征多项式的系数本身就是一件十分困难的事情。本文利用分叉理论，基于电力系统动态模型用仿连续法追踪解流形，而后将系统雅可比矩阵特征值复平面进行特定的映射变换，从而只需了解映射后特征复平面上的最大模特征值的表现，即可确定系统动态稳定性性态。

1 一般电力系统动态模型的数学描述

一般电力系统可用微分—代数方程组描述为式中：x表示系统微分状态变量；y表示系统代数状态变量；λ为控制参数。

所有满足方程（2）的点（x0，y0，λ0）称为系统（1）的平衡点

于是平衡解流形可以表示为

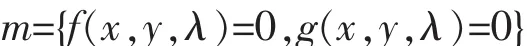
为了考察系统（1）的动态稳定性，在平衡点（x0，y0，λ0）处对式（1）线性化，以得到扰动方程

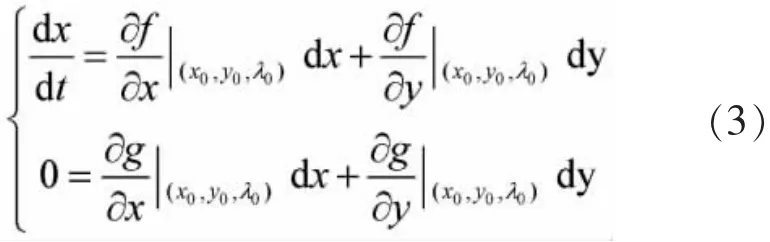
由式（3）进行消元，即可得到描述系统动力学特性的微分状态方程组：

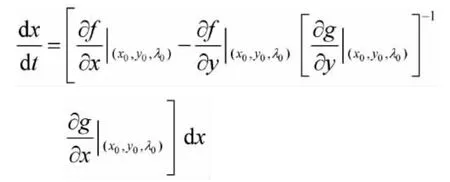
或简记为

令

根据动力学知识，系统的动态稳定性完全可以由系统雅可比矩阵J的特征值确定。

2 确定动态系统平衡点分叉值的仿连续法

对于系统（1）为了考察系统动态稳定性，将其平衡解流形m上的点分类为：

a.正则点：当雅可比矩阵J（x0，y0，λ0）的特征值无零实部时，对应的平衡点称为解流形m上的正则点。

b.鞍结分叉点：当雅可比矩阵随着控制参数的变化，有一个特征值在复平面上沿实轴从左半平面穿越虚轴时（即雅可比矩阵有零特征根时）对应的平衡点称为解流形m上的鞍结分叉点。

c.Hopf分叉点：当雅可比矩阵随着控制参数的变化，有一对共轭复特征值在复平面上从左半平面穿越虚轴时（即雅可比矩阵具有一对零实部的共轭复特征值）对应的平衡点称为解流形m上的Hopf分叉点。

延拓算法求取方程（2）的解流形m的方法是：用从初始点（x0，y0，λ0）出发的一点列（xi，yi，λi）来逼近该光滑曲线m。其中包括对点列（xi，yi，λi）进行预测、修正和步长控制等步骤。因而仿连续法确定动态平衡点分叉值的流程为：

1）设置迭代初始值i=0。

2）预测：从点（xi，yi，λi）出发给出曲线上的下一点（xi＋1，yi＋1，λi＋1）的预测值

3）修正：对上述预测值进行修正。

4）控制步长。

5）检测解流形m在相邻两点间是否有分叉出现。如有，用插值法确定更高精度的参数分叉值。否则令i=i+1，转步骤2。

下面对算法中的步骤2~5进行详细的说明论述。

2.1步骤2

2.2 步骤3

记X＝（x，y），则解流形m可以表示为

本文采用正交平面连续法来构造方程G（X，λ） =0，即过预测值做过点（Xi，λi）的曲线m的切线的垂直平面，垂直平面与曲线的交点就是所求的精确值，所以其联立方程组如下：

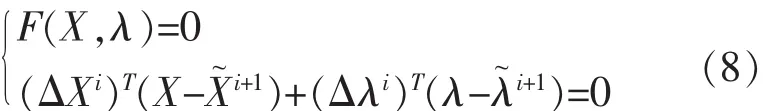
用Newton迭代法来求解联立方程（8），迭代收敛值即为曲线m上的下一点（Xi+1，λi+1）。

2.3 步骤4

步长的选取是非常重要的，它可以直接影响到计算的成败：如果步长取得过大则求取的曲线的精确度就会太低；如果步长选的过小，就会花费过多的时间。所以，我们采取控制步长的策略是：采用自动变步长的方式。所谓自动变步长就是指在迭代的过程中，按照一定的规律为之设定一个合适的步长，并且这个步长在整个迭代的过程中，根据情况不断的变动，以适应求解的需要。例如，在步骤2的修正过程中，若Newton迭代在经过预先指定次的迭代后仍不能收敛，则须减小步长来重新修正。

将式（6）在（Xi，λi）处按照傅立叶级数展开，得

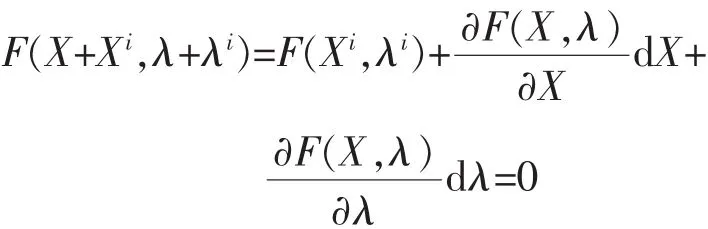
又因为F（Xi，λi），所以可得：

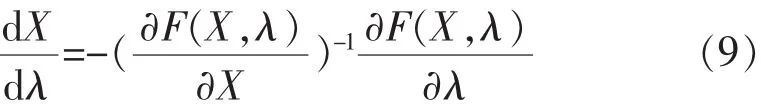
初始步长可以选取：

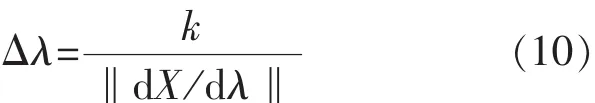
式中，k为一个经验常数，根据系统的不同，确定其值。

2.4 步骤5

为了在追踪解流形m的过程中能够检测与确定鞍结分叉和Hopf分叉点，需要构造一个判断函数。为了避免计算雅可比矩阵J的所有特征值，引入变换：

其中，I为与J同阶的单位矩阵。

不难证明Z，J矩阵的特征值具有如下的映射关系：

从上式可以看出，经过这样的变换，将J的特征值所在复平面上的虚轴映射成Z的特征值所在复平面上的单位圆。下面来证明当Z的最大摸大于1时，则J的特征值就会有在复平面的右半平面的。设 μJ＝ε±iy

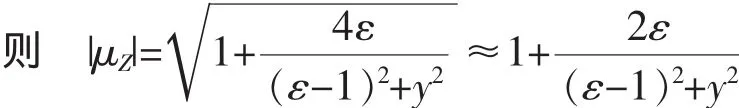
由式（14）可知，当ε<0时，｜μZ｜－1<0；反之｜μZ｜－1> 0。因此当系统处于稳定状态时，Z的模小于1。随着控制参数的变化，一旦J的特征值有一对共轭复特征值率先由左半平面穿越虚轴进入右半平面，则可以断定矩阵Z有与之对应的一对共轭复特征值由单位圆内穿出单位圆。

反之若矩阵Z有一对共轭最大模特征值为：μZmax=α±iβ，可以由反映射式：

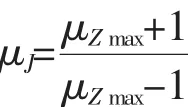
推得：

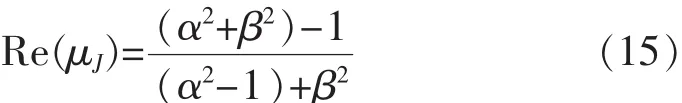
由式（15）容易看出：当矩阵Z的最大模特征值在单位圆内（即（α2＋β2）<1时），恒有 Re（μJ）<0成立。当μZmax率先穿出单位圆（即（α2＋β2）>1时），恒有Re（μJ）>0成立。因此令

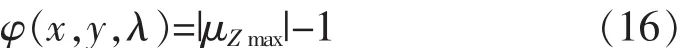
当 φ（xi，yi，λi）·φ（xi＋1，yi＋1，λi＋1）≤0时，在这两点之间的区间里发生了状态的改变，必有一分叉点出现，当μZmax＝－1时，是鞍结分叉点，当只有｜μZmax｜＝1，则系统发生Hopf分叉。可用插值法在 （xi，yi，λi）和（xi＋1，yi＋1，λi＋1）之间确定更高精度的分叉点。

3 算例

利用本文所介绍的方法来确定如图1所示的简单系统的分叉点。网络发发电机的参数同文献［2］。该系统由一个负荷母线和两个发电机母线组成，其中一个发电机母线被处理成松弛母线。

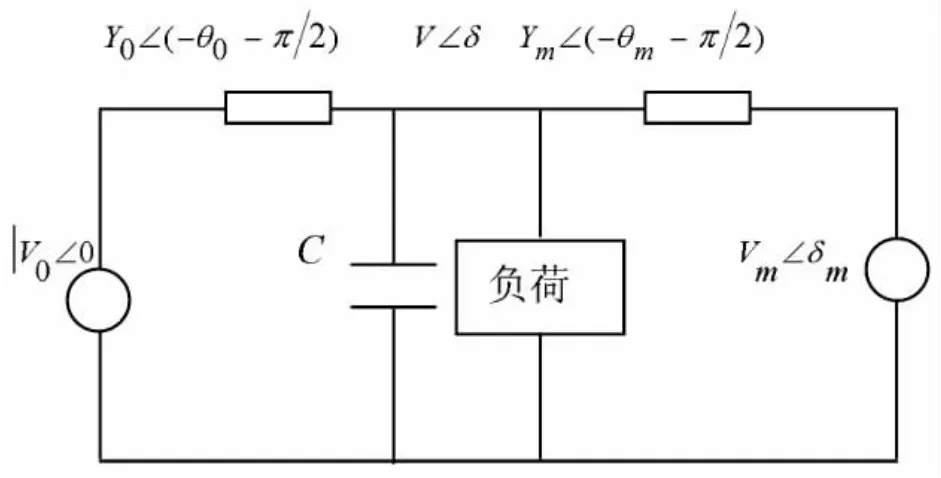
图1 简单电力系统

非松弛母线发电机2用如下的摇摆方程描述：

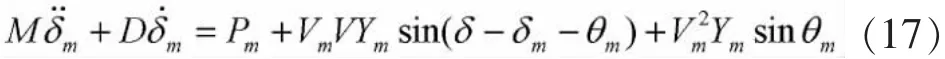
式中，M，D，Pm分别为发电机2的惯性常数、阻尼和机械输入功率。将包含电容器C的电路进行戴维南等效，则其等效电压V′0，等值电导Y′0，阻抗角θ′0分别为

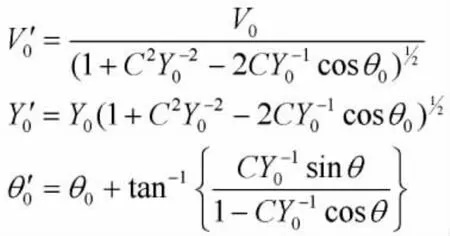
本文节点3的负荷模型采用考虑静态负荷和动态异步电动机负荷综合组成，其描述方程如下：

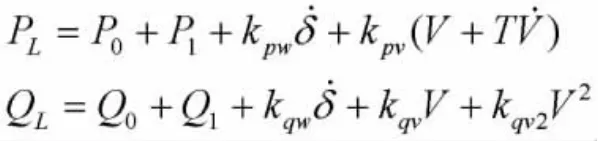
式中，P0，Q0是异步电动机的恒定有功和无功功率；P1，Q1是恒P－Q负荷。

可得该系统的状态方程为

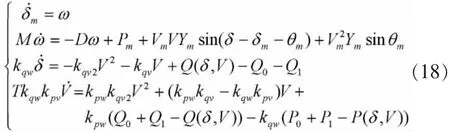
系统微分状态变量为：x=（δm，ω，δ，V）；控制参数选为：λ＝Q1。

用本文所述方法计算系统（18），初始点Q1＝10，此时系统（18）的平衡点为（δm，ω，δ，V）＝（0.2858165，0.0，0.1066416，1.22951939），计算得到的鞍结分叉点和Hopf分叉点如表1所示。

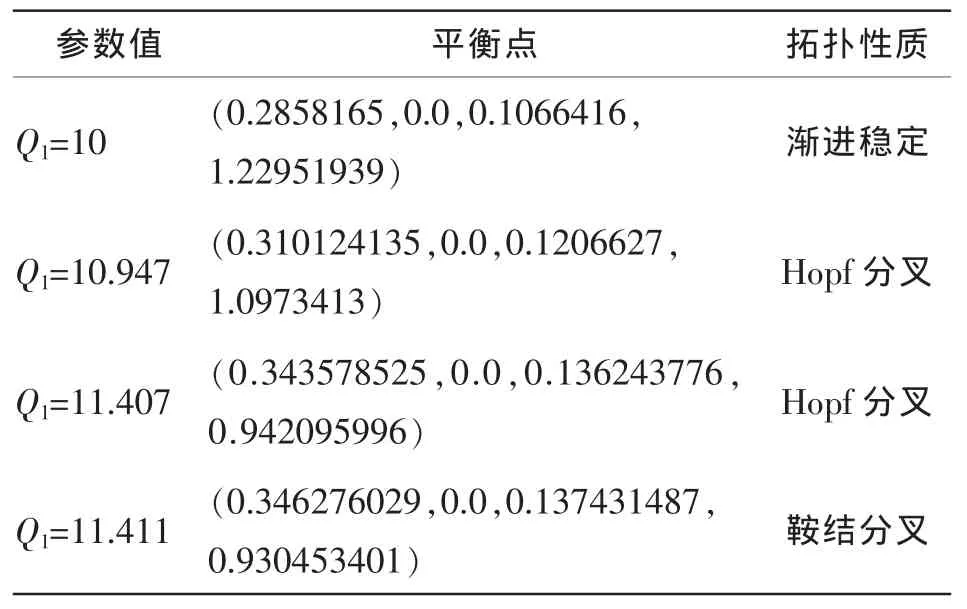
表1 鞍结分叉点和Hopf分叉点

从表中可以看出，系统经过了两次Hopf分叉，在Q1=11.411时，发生鞍结分叉，系统崩溃。由此可以证实在考虑电压动态稳定时，不能只考虑鞍结分叉，用此作为系统不稳定的判断条件，而应该综合考虑各种可能出现的动态分叉情况，从而真实的判断系统何时发生电压失稳。

下面我们综合考虑P1，Q1变化时，系统发生分叉的情况。我们将计算所得的Hopf分叉点和鞍结分叉点的轨迹，投影到P1-Q1平面上如图2所示。

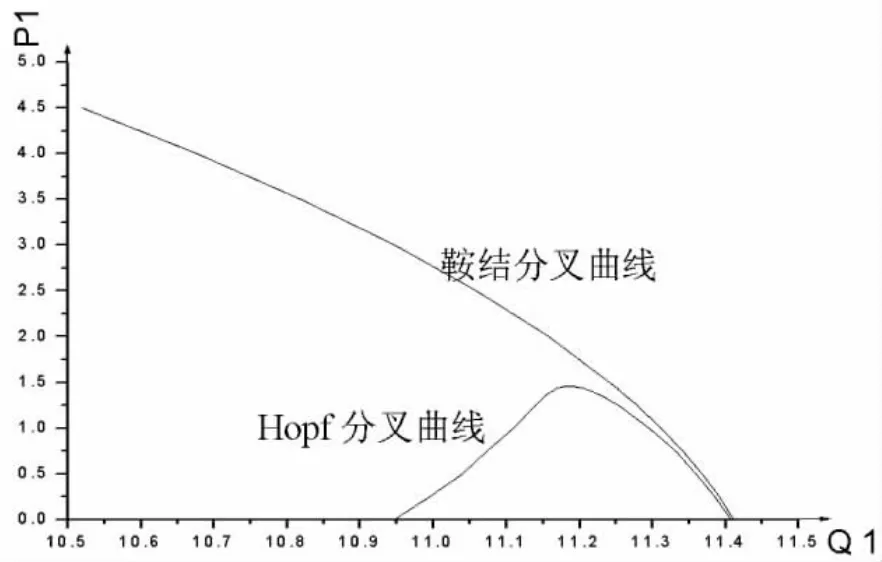
图2 双参数分叉图

从图2可以看出，在参数P1从0开始的一定范围内，Hopf分叉点有两支。当给定有功负荷P1时，则随无功负荷Q1的变化，系统将经历2个Hopf分叉点，然后到达鞍结分叉点；随着参数P1的不断增大，这两支Hopf分叉逐渐接近，最后重合，此时沿无功负荷的增长，只出现一个Hopf分叉点；而如果有功负荷再进一步增大，系统将不会出现Hopf分叉点，在鞍结分叉点系统失稳。

5 结论

重点论述了确定动态系统的Hopf分叉和鞍结分叉点的仿连续法的实现方法和技术。该法在确定分叉点时，只需了解映射后的矩阵的最大模特征值就可以确定系统的动态稳定性。它的计算量小，适用面广。用一个典型的电力系统验证了本方法的可行性和实用性。

［1］Harry G K，Arun K P，Leon Y B.Static Bifurcation in Electric Power Networks：Loss of Steady-State Stability and Voltage Collapse.IEEE Trans on CAS，1986，33（10）.

［2］Dobson I，Liming L，New Methods for Computing a Closest Saddle Node Bifurcation and Worst Case Load Power Margin for Voltage Collapse.IEEE Trans on Power System，1993，8（3）.

［3］Harry G K，Fischl R F，Nwankpa C O.Local Bifurcation in Power System：Theory，Computation and Application. In：Proceedings of the IEEE.1995，83（11）.

［4］彭志炜，胡国根，韩祯祥.电力系统负荷电压稳定性研究［J］.电力系统自动化，1997，21（7）.

［5］彭志炜，胡国根，韩祯祥.电力系统负荷电压稳定性研究［J］.电力系统自动化，1997，21（8）.

［6］彭志炜，胡国根，韩祯祥.应用分支理论研究电力系统电压稳定性［J］.电力系统自动化，1997，21（2）.

［7］Dobson I，Chiang H D.Towards a Theory of Voltage Collapse in Electric Power Systems.Systems and Control Letters，1989（13）253-262.

［8］Abed E H，Wang H O，Alexander J C.Dynamic Bifurcations in a Power System Model Exhibiting Voltage Collapse.International Journal of Bifurcation and Chaos，1993，3（5）：1169-1176.

A New Method for Computing the Voltage Bifurcation Point of Power System

Based on power system dynamic model，an effective method is proposed to solve the saddle-node bifurcation or hopf bifurcation point in this paper.The principle of this method is when the parameter of dynamic system varies slowly，its balance point is extended correspondingly.During this process，the dynamic voltage stability is determined by inspecting the alternation of the system topology character in the local range of balance point，and then the interpolation method is applied to further determine the value of parameter when bifurcation occurs.Numerical results of typical voltage stability model have shown that this method is effective and practical.

saddle-node bifurcation;hopf bifurcation;imitating continuation method;dynamic voltage stability

book=1,ebook=1

TM712

A

1007－9904（2010）04－01－05

2010－03－25

井雨刚（1979-），男，硕士，工程师，主要从事继电保护现场调试工作。