关于严格伪压缩映射与均衡问题的一个修正迭代格式
黄丽月,胡艳芳,陶 燕
(红河学院数学学院,云南蒙自661100)
关于严格伪压缩映射与均衡问题的一个修正迭代格式
黄丽月,胡艳芳,陶 燕
(红河学院数学学院,云南蒙自661100)
在Hilbert空间,论文给出了关于严格伪压缩映射与均衡问题的一个修正的迭代格式.在迭代参数满足新的条件下,获得了一个强收敛定理,所得结果是相关文献结果的补充和完善.
严格伪压缩映射;不动点;均衡问题;强收敛
0 引言
设表示实Hilbert空间,〈.,.〉和‖.‖分别表示它的内积及范数,是的非空闭凸子集.设映射Φ:C×C→R(其中是实数集).关于Φ的均衡问题(简称EP)是指:找一个元x∈C使得

设EP(Φ)表示问题(1)的解集.如果,Φ(x,y)=〈Ax,y-x〉,其中映射A:C→H是非线性算子,则问题(1)退化为经典变分不等式问题:找一个元x∈C,使得

设T是H中的映射,D(T)和R(T)分别表示T的定义域和值域,F(T)表示T的不动点集,F(T)={x∈D(T):Tx=x}.如果‖Tx-Ty‖≤‖x-y‖,∀x,y∈D(T),则称T是非扩张映射;如果存在常数k且0≤k<1,使得

则称T是k-严格伪压缩映射.显然,非扩张映射是0-严格伪压缩映射.通过迭代逼近方法,许多作者讨论了均衡问题(1)与某些非线性算子不动点问题的公共逼近解,例如文献[1-4].在文献[1]中,曾六川等建立了关于k-严格伪压缩映射的迭代格式

其中{an},{rn}是非负实数列且满足{an}⊂[a,β](a,β∈(k,1))和>0.曾六川等获得下面的结果:
定理C1[1]设C是H的非空闭凸子集,映射Φ:C×C→R满足(A1)-(A4)(见第二节),T:C→C是k-严格伪压缩映射且(T)∩EP(Φ) Ø.设x1∈C,{xn}和{un}迭代格式(3)产生的序列.若(3)的迭代参数an, rn满足条件:(i){an}⊂(a,β),a,β∈(x,1);(ii)>0.则{xn}和{un}分别弱收敛于P∈F(T)∩EP(Φ).
定理C2[1]设C是H的非空闭凸子集,映射Φ:C×C→R满足(A1)-(A4)(见第二节),T:C→C是k-严格伪压缩映射且F(T)∩EP(Φ) Ø.设x1∈C,{xn}和{un}是迭代格式(3)产生的序列.若迭代格式(3)的迭代参数an,rn满足下面的条件:(i),{an}⊂(a,β),a,β∈(k,1);:(ii)(xnF(T))∩EP(Φ))=0,其中
d(xnF(T))∩EP(Φ))表示xn到F(T))∩EP(F))的距离.
为了证明本文的结果,需要介绍下面的预备知识.
1 预备知识
设H表示实Hilbert空间,则对于任何λ∈[0,1]和∀x,y∈H有


则 (1)Tr是单值的;
(2)∀y∈H,有‖Tr(x)-Tr(y)‖2≤〈Tr(x)-Tr(y),x-y〉
(3)F(Tr)=EP(Φ)
(4)EP(Φ)是非空闭凸集.
引理1.4设∀x,y∈H,则‖x+y‖2≤‖y‖2+2〈x,x+y〉.
引理1.5[7]设{an}是非负实数列并满足
ax+1≤(1-an)an+anσn+yn,n≥0
若(i)an∈[0,1],Σan=∞,(ii),lim supσn≤0,(iii)yn≥0,Σyn<∞,则当n→∞,an→0.
引理1.6[8]设C是实H ilbert空间的闭凸子集,T:C→C是k-严格伪压缩映射,则I-T是半闭的,即当xn弱收敛于x和(I-T)xn强收敛于y时,x∈C和(I-T)x=y,其中I是恒等映射.
2 定理及其证明
定理2.1设是C实H ilbert空间H的非空闭凸子集,映射满足条件Φ:C×C→R满足条件(A1)-(A4), T:C→C是k-严格伪压缩映射(其中0≤k<1),EP(Φ)∩F(T)≠Ø,定义序列{xn}和{un}为:

其中v,x1∈C,σ∈(0,1-k),an∈(0,1),an,βn,rn满足下列条件:
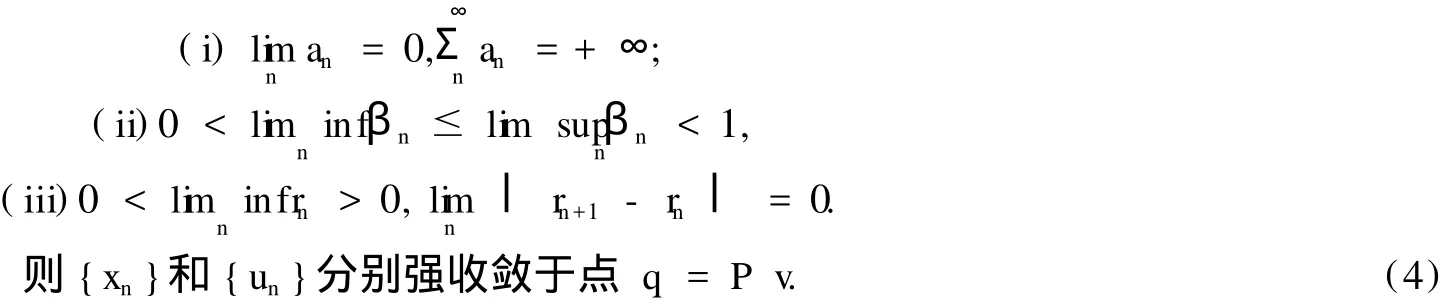
证明.首先证明{xn}有界.设u∈◊,由于T是k-严格伪压缩映射,因此从(4)式得到:

另一方面,从引理1.3知un=Tynxn,因此‖un-u‖≤‖Tynsn-Tyn‖≤‖xn-u‖,于是
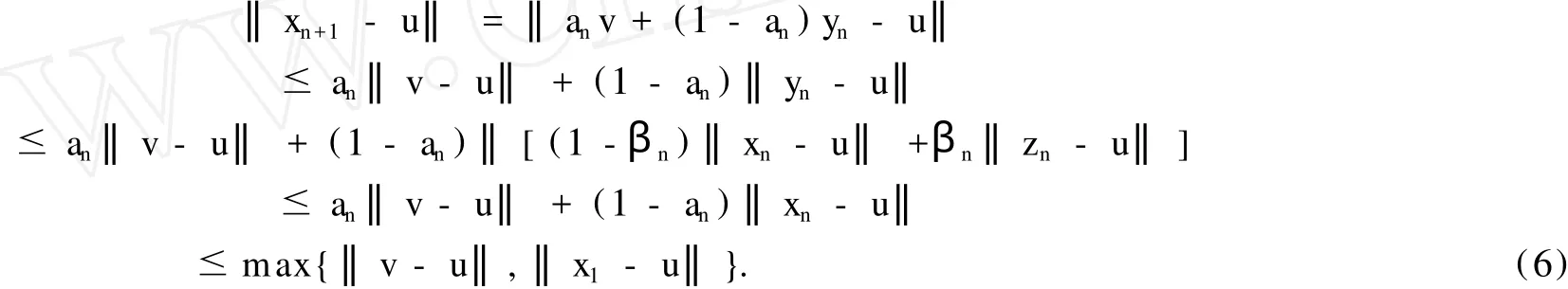
上述(6)式可用数学归纳法证明,这里略去.从(6)式可知{x}界.因此,{y}和{z}也有界.

由un=Trnxn和引理1.3得

和

在(9)取yn+1和在(10)取y=u可得

和


致 谢:
首先,衷心感谢大学生科技创新基金的支持.其次,在本文的撰写过程中,何振华老师作为我的指导老师,他严肃的科学态度,严谨的治学精神,精益求精的工作作风,深深地感染和激励着我.他给予我细心的指导和不懈的支持,在此衷心的感谢何老师.
〔1〕L.-C.Ceng,S.Al-Homidan,Q.H.Ansari,J.-C.Yao,An iterative scheme for equilibrium problems and fixed pointproblems of strict pseudo-contraction mappings[J],Journal of Computational and AppliedMathematics,2009,15:967-974
〔2〕A.Tada,W.Takahashi,Strong convergence theorem for an equilibrium problem and a nonexpansive mapping[J],Optim.Theory Appl.,133(2007)359-370.
〔3〕XiaolongQin,Shih-sen Chang,Yeol JeCho,Iterative methods for generalized equilibrium problems and fixed point problemswith applications[J],NonlinearAnalysis,doi:10.1016/j.nonr wa.2009.10.017.
〔4〕P.L.Combettes,S.A.Hirstoaga,Equilibrium programming in Hilbert space[J],Nonlinear convexAnal.6(2005)117-136.
〔5〕Tomonari Suzuki,Strong convergence theorems for infinite families of nonexpansive mappings in general Banach spaces[J],Fixed
book=8,ebook=194
O17
A
1008-9128(2010)04-0037-06
2010-05-21
红河学院大学生科技创新基金(SSTIF0936)。指导教师:何振华
黄丽月,女,红河学院数学学院06级数学与应用数学A班.

