平面管网水力计算及实现方法

□刘建红 □张新伟 □王文先

(黄河勘测规划设计有限公司)

平面管网水力计算及实现方法

□刘建红 □张新伟 □王文先

(黄河勘测规划设计有限公司)

水力计算是进行给水或配水管网技术经济比较的基础。环状管网水力计算的核心是联立求解连续性方程、能量方程和压降方程。阐述了平面环状管网水力计算原则，根据数学模型编制了基于Excel和V i sual Basi c计算或程序代码，并以实例进行了计算验证。

Exce；V i sual Basi c；平面管网；环状管网；水力计算

一、概述

给水或配水管网的费用(包括管道、阀门及附属设施)约占工程总投资的60%～80%，而且运行中消耗大量的能源，因此在方案设计阶段需要进行经济技术比较，而水力计算结果是进行比较的基础数据。本文在阐述管网水力计算原则的基础上，以实例探索了基于Excel和Visual Basic平台的计算方法。

二、环状管网水力计算原理

环状管网的水力计算是联立求解连续性方程、能量方程和压降方程。

连续性方程(节点方程)：任一节点，流向该节点的流量等于从该节点流出的流量,规定从节点流出的流量为正，流向节点的流量为负；

能量方程(环路方程)管网任一环路内，各管段水头损失之和等于零(实际计算时以计算精度控制)，即任两节点之间各管段的水头损失相等，并规定水流顺时针方向管段的水头损失为正，逆时针方向为负；

压降方程(管段方程)表示各管段流量和水头损失的关系。

设某环状管网的管段编号为i=1…im，环路编号为j=1…jm，结点编号为k=1…km，管段数与节点数关系为i=j+k-1。设各管段的流量和沿程水头损失分别为Qi、hfi，各结点的供水流量为qk。连续性方程和能量方程表达式为：

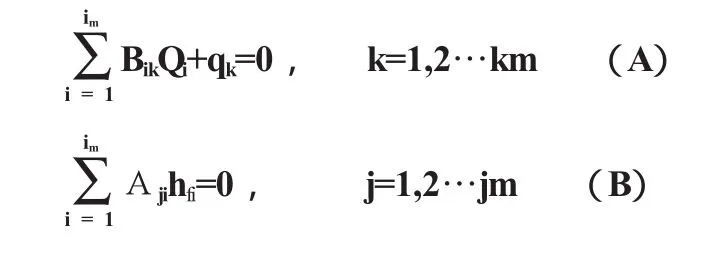
式中Aij、Bik为控制系数。

当管段i不在环路j中，则Aji=0；当环路j中管段i的流动方向为顺时针方向，Aji=1，否则Aji=-1；

当管段i与结点k无直接联结时，则Bik=0；当结点k处管段i的水流方向为流出结点，Bik=+1，否则Bik=-1。

对于截面为圆形管道，由达西公式及流速计算公式hf=λ，经变换整理经变换整理：

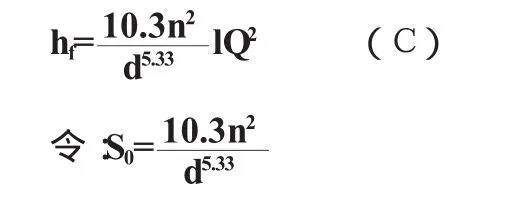
公式(D)即管段 i的压降方程。公式(C)、(D)中，n、d 及 l分别为管道的糙率、管径及长度。

式(A)、(B)、(D)可以组成由i+j+k=2i个独立的方程组成的方程组，可以求得2i个未知变量Qi及hfi。

在管网供水图上注明节点的流量后，根据供水情况，用箭头表示各管段的水流方向并进行流量分配，使其满足式(A)关系。根据管段流量及确定的流速选择管径，即可进行水力计算。

初步计算出的环路水头损失一般不能满足方程(B)，即环路水头损失闭合差不满足设定精度为设定精度，如0.001m)j=1,2…jm(E)

因此需要对初设流量进行修正，环路j的修正流量为ΔQj的计算式为

修正后各管段流量为(公共管段考虑相邻环的修正流量)：

如果流量修正后，仍不满足精度要求，则需要继续修正，直至满足方程(E)。

三、环状管网水力计算实现方法

（一）基于Excel平台计算方法

在图1所示的环状管网中，各管段的长度、管径见表1(数据行号：3，4行)，糙率均为0.0125，各结点的供水流量如图1示。

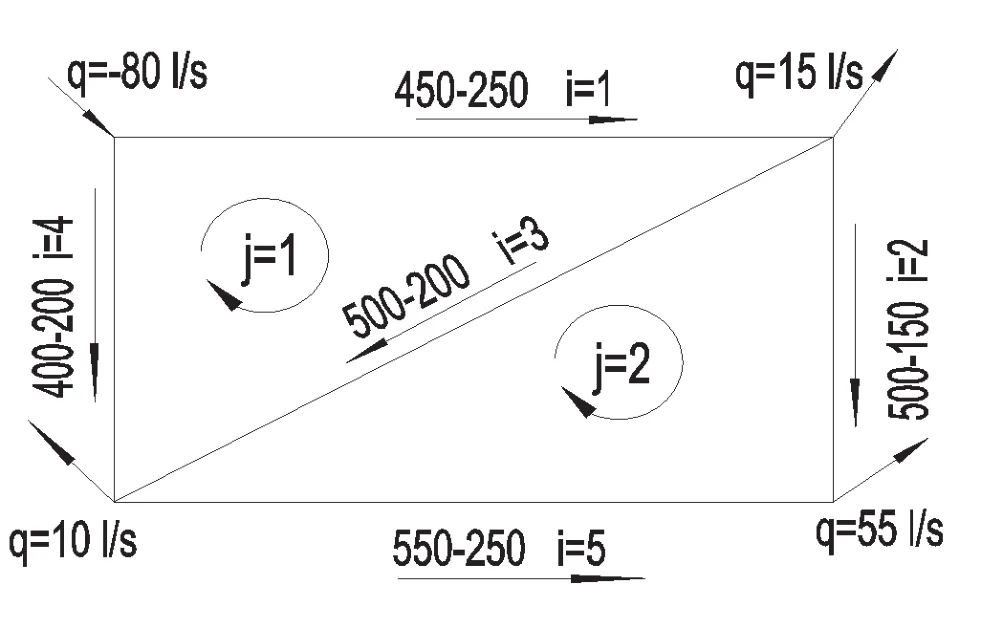
图1 环状管网（示例）

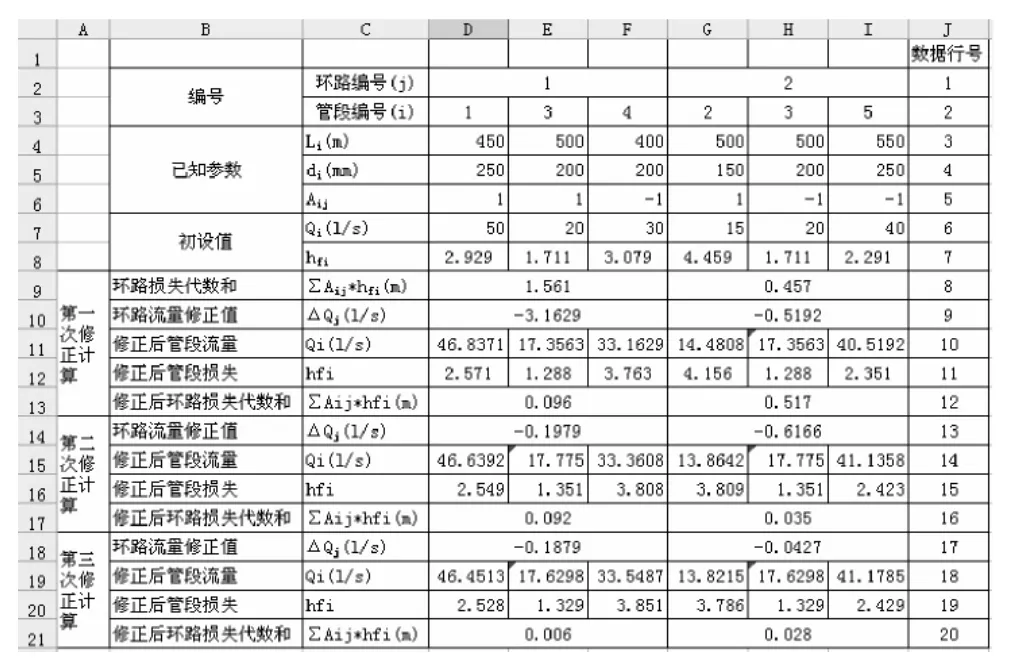
表1 Excel水力计算界面

各管段水流方向(如图)及流量大小Qi，并满足方程(B)，见表1(6行)。根据水流方向确定系数Aji，见表1(5行)。

计算代码设计如下(以第一环路第一次修正为例)：

1.根据方程(C)计算各管段沿程水头损失hfi，见表1(7行)；

2.根据方程(B)计算各环路的水头损失闭合差ΣAjihfi见表1(8 行)；

3.根据方程(F)计算各环路的修正流量为ΔQj，见表1(9行)；

4.根据方程(G)对各管段流量进行修正，见表1(10行)；

5.判断各环路水头损失闭合差是否满足精度要求。若不满足，重复1～4步计算，直至各环路水头损失闭合差满足精度要求。本算例经3次修正各环的闭合差已满足要求。

可见采用Excel进行管网的水力计算，界面清晰、计算过程明确，能达到计算的精度要求。但是，当管网环路增多时，计算代码设计繁琐，易于出错。

（二）基于Visual Basic计算方法

1.主要变量定义

2.程序代码

3.结果输出

输出结果以顺序方式存入名为endlist.txt文件，可以实现打印输出。

第1环路闭合差(m)：1.66893E-06

第2环路闭合差(m)：5.245209E-06

环路修正次数为(次)9。

第1段管路的流量(l/s)和损失(m)：46.42558 2.525598

第2段管路的流量(l/s)和损失(m)：13.78234 3.764497

第3段管路的流量(l/s)和损失(m)：17.64325 1.331356

第4段管路的流量(l/s)和损失(m)：33.57442 3.856953

第5段管路的流量(l/s)和损失(m)：41.21766 2.433135

四、结语

一是式(C)是由达西公式结合满宁公式推求的，对于混凝土或钢筋混凝土管材(糙率n为0.013或0.014)有良好的适用性。对于其他管材，应采用专业规范或手册推荐的水力坡降计算公式计算管路的水力损失，水力坡降与管路比阻关系。此外，为简化计算，没有计及管网的局部水力损失；二是采用Excel或Visual Basic编程均可达到所需的精度。但若实现大型管网的高精度、快速的计算必须采用类似于VB的具有循环和控制转向的编程语言。

2010-05-09

刘建红（1969-），女，重庆涪陵人，高级工程师，从事水电站及给排水设计。