ERP事件相关成分分解算法研究

尹 刚 刘铁军

(电子科技大学生命科学与技术学院，神经信息教育部重点实验室，成都 610054)

ERP事件相关成分分解算法研究

尹 刚 刘铁军*

(电子科技大学生命科学与技术学院，神经信息教育部重点实验室，成都 610054)

当单次实验记录中包含两个或多个事件时，以不同事件时间为参考得到的事件相关电位(ERP)将导致不同事件相关的ERP成分之间形成交叉干扰，从而影响对ERP成分的正确理解。为了恢复真实的事件相关成分，Zhang(1998)提出了一种两个事件成分分解的算法。本研究中首先分析该算法的特点，发现其对边界条件的选取非常敏感，采用周期性边界条件的计算结果明显好于非周期边界条件的计算结果，同时发现该算法对事件时间分布形状并不敏感，仿真结果显示采用高斯分布和均匀分布的事件时间能得到相类似的结果，但算法对事件时间分布的方差也较敏感，方差越大分解的效果越好。其次，扩展两个事件成分分解的算法到3个和多个事件成分的分解。最后应用多成分分解算法到真实实验数据(3事件——提示，刺激，反应)，结果显示，事件“提示”引起的ERP波形在提示后大约500 ms后回到基线水平，符合心理学过程，并且有助于心理学实验设计。

事件相关电位;刺激成分;反应成分;线性卷积;循环卷积

Abstract:If a single trial includes two or more events，the cross-contamination of these different events related components may mislead the explanation of ERP.In order to recover each event related component，Zhang(1998)proposed a method for two events related problem.In our work，the two event related components decomposition algorithm was evaluated at first.We found that the method was very sensitive to the convolution calculation，and the circular convolution was much better than the linear convolution in recovering the true event related component.For the event time distribution，the algorithm was insensitive to the shape of the distribution，with a similar result for both Gauss and Uniform，but sensitive to the variance of the distribution.Then we extended the method to the situation of three or more events involved in a single trial.The proposed method was applied to a true experiment data(three events;including cue，stimulus and response)，the results showed that the cue-component waveform turned out to be almost flat after cue-onset 500 ms，being reasonable and meaningful for experimental design and fit well with the physiological processing.

Key words:eventrelated potentials;stimuluscomponent;responsecomponent;linearconvolution;circular convolution

引言

通常事件相关电位(event related potential，ERP)可以通过迭加平均多次以特定事件作为时间参考的单次实验记录而得到，如果特定的事件是刺激，那么把迭加平均得到的 ERP叫做刺激对齐(stimulus-aligned)ERP，比如 P300［1-2］，N400［3］，如果迭加平均以反应作为事件时间参考，把迭加平均得到的ERP叫做反应对齐(response-aligned)ERP，如错误相关负电位(error-related negativity，ERN)［4-5］、单侧化准备电位(lateralized readiness potential，LRP)。然而，如果单次实验记录中既有刺激事件又有行为反应事件，那么以刺激时间为参考得到的叠加平均ERP，即包含由刺激引发的刺激成分又包含由行为反应引起的反应成分，反之亦然，这种交叉干扰将影响对ERP成分的理解。

在研究心理学过程中，由于刺激成分和反应成分的交叠导致了对一些认知过程的神经机制理解的分歧，例如，在研究反应抑制的过程中，关于 GO和 NOGO差异成分N2/P3是否来源于由于GO过程中的运动响应成分引起了广泛的争论［6-7］.与此相类似的，这种刺激成分和反应成分的交叠也存在于 LRP［8］和 ERN［4-5］的研究中。除此之外，在研究视觉空间注意时，一个外周或中心提示被使用，当要求被试做出行为反应时，那么单次的实验记录将包含提示、刺激和反应3个事件，因此拓展两成分分解算法到3个或多个事件成分算法是有必要的。

在本研究中，首先仿真研究了边界条件的选取和事件时间分布对两事件成分分解算法结果的影响，然后扩展算法到3个或多个事件成分分解。最后应用多事件成分分解算法到真实实验数据(实验中有3个事件参与)。

1 方法

1.1 两事件成分分解

假设有如下实验数据:

1)实验数据包含 N个单次‘trial’，每个单次‘trial’均有两个事件参与，即外部刺激和被试的行为反应，每个‘trial’中外部刺激出现的时间是一致的，而被试的行为反应时间是不一致的。

2)以刺激事件为参考时间的平均ERP(stimulus-aligned ERP)Fs(t)。

3)以被试行为反应时间为参考时间的平均ERP(response-aligned ERP)Fr(t)。

4)反应时的概率分布g(t)---相对于外部刺激出现的时间而言，所有单次‘trial’中被试行为反应时间的概率分布。下面将分析如何恢复真实的刺激成分(S-component)fs(t)和真实的反应成分(R-component)fr(t)。数学上，有两个方程［9］

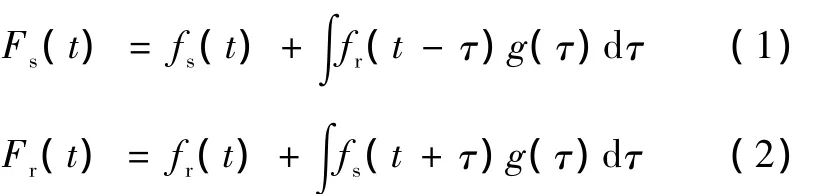
转化为卷积形式，得到

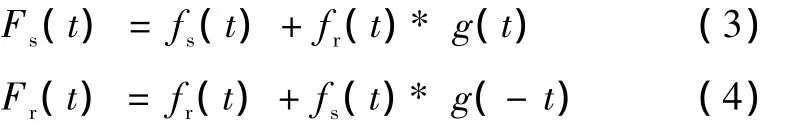
通过傅立叶变换，可得到唯一解

～代表频域信号。

1.2 边界条件

在计算卷积的时候或计算以不同事件时间为参考的迭加平均的时候，由于信号是有限长度，信号开始以及结束的部分数据点由于时移过程将丢失，通常有两种边界条件来处理这种问题，一种是周期边界条件—就是以周期条件弥补丢失的数据点，相对应的卷积计算就是循环卷积(circular convolution，CC)，另一种是非周期边界条件—就是以补零的方式弥补丢失的数据点，相对应的卷积计算就是线性卷积(linear convolution，LC)。

当采用周期边界条件的时候，卷积计算对应的就是循环卷积，对于时域卷积式 (3)和式(4)，可以转化为如下的时域矩阵方程

或

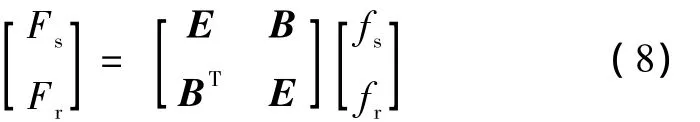
如果采用非周期边界条件，对应的卷积就是线性卷积，式(8)中的B将变为如下形式

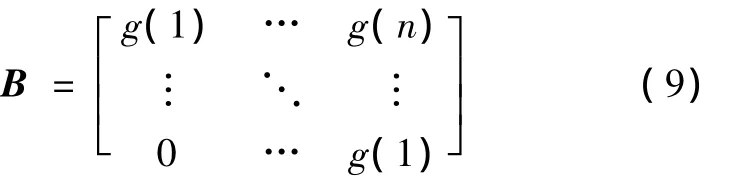
对于循环卷积，能得到式(8)的频域表达方式

然而，对于线性卷积，其计算只能在时域内进行。

1.3 3事件成分分解

1.3.1 3事件成分分解的基本思想

假设信号中包含3个不同的事件相关的成分，假定这3个成分分别为fc，fs，fr，假设这3个事件开始呈现的时间分别为tc，ts，tr并有如下关系 tc＜ts＜tr。当选择tc作为参考时间(所有‘trial’以 fc呈现的时间tc为基准对齐)，ts和 tr相对于 tc的概率分布分别定义为g1(t)，g2(t)(事件时间的概率分布和两事件情况类似，以其中一个事件时间为参考时间，另外事件时间相对于参考事件时间的概率分布)，当选择 ts作为参考时间(所有‘trial’以 fs呈现的时间ts为基准对齐)，tc和 tr相对于 ts的概率分布分别为g1(-t)，g3(t)，当选择 tr作为参考时间(所有‘trial’以 fr呈现的时间 tr为基准对齐)，tc和ts相对于 tr的概率分布分别为g2(-t)，g3(-t)。假设信号 Fc，Fs和 Fr是分别为以 tc，ts，tr作为参考时间时得到的迭加平均 ERP，fc，fs，fr与信号 Fc，Fs和 Fr的关系如下［10］

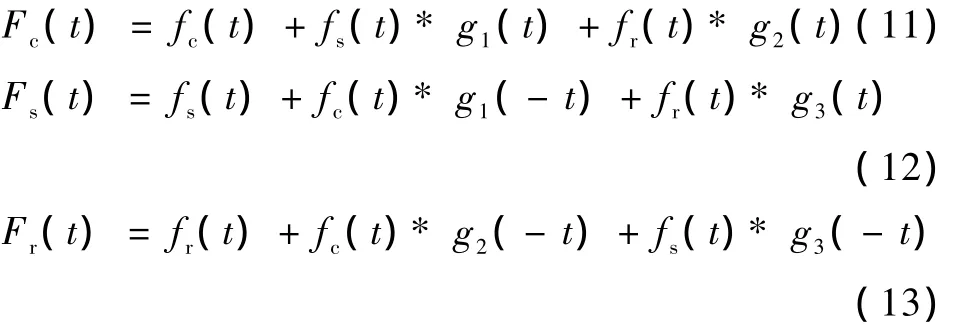
1.3.2 两种不同的边界条件

对于周期性的边界条件，此时的卷积计算为循环卷积，有

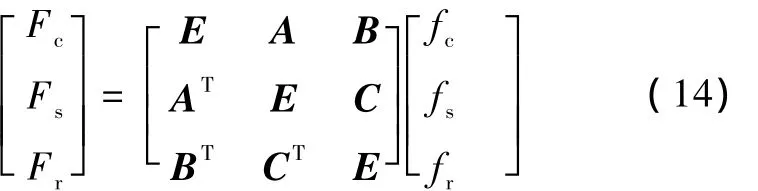
其中

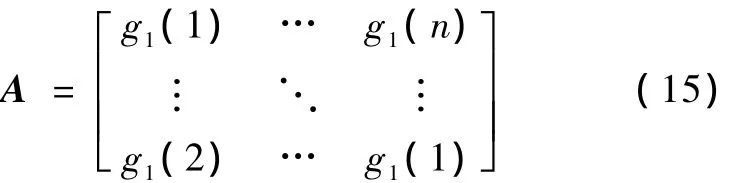
矩阵B、C和 A是类似的，矩阵中相应的元素变为g2、g3。对于非周期性的边界条件，此时的卷积计算为线性卷积，方程(14)中的A变为

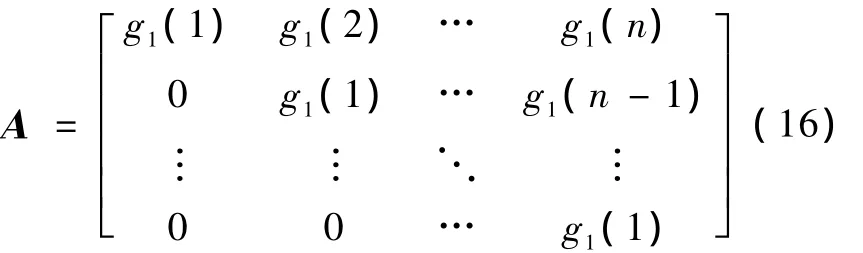
矩阵B、C和 A是类似的，B、C矩阵中相应的主对角线上的元素变为g2、g3，主对角线下的元素都为0对于循环卷积，式(14)在频域内的表达如下

而对于线性卷积，其计算只能在时域内进行。

1.4 多事件成分分解

当信号中包含多个不同事件的时候，可计算出以任意一个事件时间为参考时间其他事件时间相对于这个事件时间的分布，得到如下关系［10］

采用周期性边界条件的时候，Gi和 Ki和式(15)中A，B或C类似的，采用非周期边界条件的时候和式(16)中 A，B或C类似。对于周期性边界条件，式(18)在频域内的表达如下

1.5 实验设计

12个健康的大学在校学生参加了本研究的实验，其中5位为女性，他们的年龄在18到23岁之间，都是右利手，并且视力正常，都没有精神疾病病史。受试者均知情同意。

实验过程如图1所示，个人电脑产生刺激图像，黑色背景中间是固定的0.5°视角的‘+’。水平位置位于‘+’左右5°视角的两边的矩形框是1.5°×1.0°视角。加亮的矩形框(左边或右边)作为‘cue’，刺激是以等概率出现在左边或右边矩形框中的短线(靶刺激)(0.75°视角)或长线(1.0°视角)。被试被安排坐在黑暗的房间，坐在距离显示器50 cm的位置，要求被试注视屏幕中央的‘+’。

开始呈现两个矩形框分别位于中央固定‘+’左右两边，呈现时间为120 ms，在此之后的1 000 ms到1200 ms 的试验间隔(inter-trial interval，ISI)，其中一个矩形框外周被加亮(cue，提示)50 ms，然后加亮消失，紧接着一个100 ms到 300 ms的随机延后靶刺激呈现200 ms。‘cue’的呈现和靶刺激的呈现都以左右两边等概率的方式呈现。要求被试当看到靶刺激的时候尽可能快地做出按键反应，靶刺激出现在左视野用左手按“1”，靶刺激出现在右视野用右手按“4”。所有被试要求在正式实验开始之前先做10次练习。

图1 实验过程中的刺激序列的展示。Cue是左边或右边外周加亮的矩形框;靶刺激是矩形框内竖直短线;cue和刺激之间的时间间隔(SOA)是100 ms到300 ms的随机值。Fig.1 An example of the stimulus display sequences used in the this experiment.The cue is a brightening of an unfilled box centered on one of the two peripheral target locations;the target is a short vertical line in the box.Interval between cue and stimulus(SOA)is a randomly variant from 100 ms to 300 ms

2 仿真

仿真参数

(1)仿真信号和噪声

所有事件相关的成分 (fc，fs，fr)通过式(20)产生［11］。

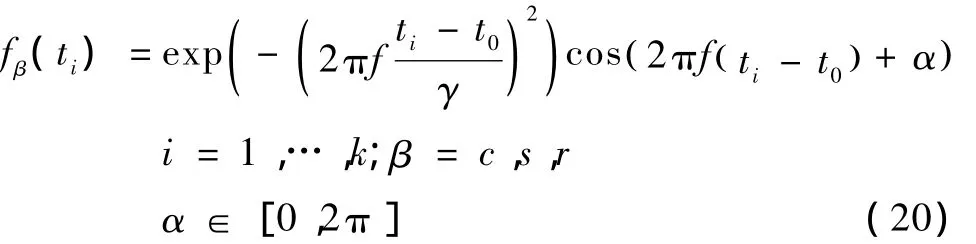
式中，ti=i*dt，dt=4 ms，k=400.对于 fc，fs，fr，γ分别为3，2.5，2。t0表示事件开始时间。高斯白噪声通过MATLAB产生。

(2)事件时间的分布.

两种事件时间分布被测试:高斯分布和均匀分布，其均值和方差将在下一节中具体给出。

(3)构建数据

在产生单次数据的时候直接通过式(20)得到。得到所有单次数据以后，在计算迭加平均时，分别以周期边界条件和非周期边界条件来计算按不同事件时间为参考的迭加平均信号。

(4)对结果的评估

采用两种评估方式:相对误差(relative error，RE)和 相关系数(correlation coefficient，Cor)，RE定义如下

这里 fs，fr仿真信号是重构信号

Cor定义如下

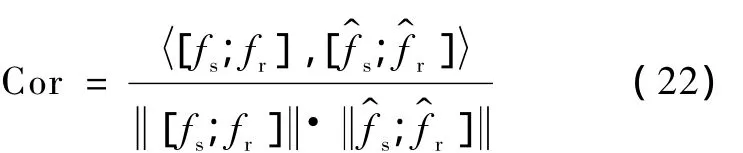
其中 〈·〉表示向量内积.

此外，信噪比SNR采用定义如下

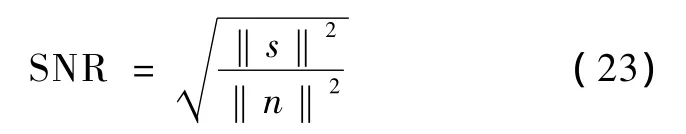
式中，s代表信号，n代表噪声。对于3事件成分分解，RE、Cor以及 SNR的定义和式 (21)～式(23)类似。

3 结果

3.1 仿真数据结果

3.1.1 两事件成分分解

假设以刺激事件时间作为事件参考，反应时的分布是高斯或均匀分布，其均值为200 ms，标准差为100 ms。对于5种不同的SNR条件，分别使用周期性边界条件和非周期性边界条件完成50次计算。α是0～2π内的一个随机数，对于 fs，f取3～4 Hz的随机值，对于fr，f取3～4 Hz的随机值。图2展示了计算结果。

从图2可以发现无论事件时间分布是高斯分布还是均匀分布，在5种不同的信噪比条件下，使用周期边界条件(CC)得到的分解结果比使用非周期边界条件(LC)得到的分解结果有更小的相对误差，有更大的相关系数，很明显使用周期边界条件(CC)比非周期边界条件(LC)能得到更鲁棒的分解结果。统计结果显示，5种信噪比条件下，两种边界条件下得到的RE以及Cor的均值都有显著性差异(P＜0.001)。上述结果表明使用周期性的边界条件(CC)能更真实的重构真实信号。

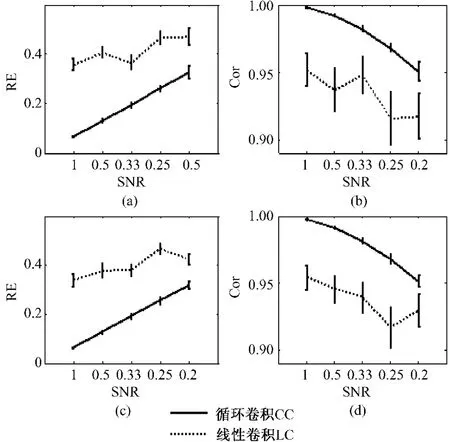
图2 在不同的信噪比(SNR)以及不同边界条件下两事件成分分解算法计算得到的相对误差(RE)以及相关系数(Cor).(a)和 (b)中事件时间分布为高斯分布，(c)和 (d)中事件时间分布为均匀分布Fig.2 The mean RE and Cor of for CC and LC under the difference SNR conditions，respectively，dot line:LC(linear convolution);solid line:CC(circular convolution).Error bar represented standard deviation of RE and Cor.(a)and(b):event time distribution is Gauss;(c)and(d):event time distribution is uniform

图3显示了一个两事件成分分解的例子，其参数为SNR=1，对 fs取 f=3.1，γ=2.5，α=3.16，对fr取f=3.62，γ=2，α=0.03.使用周期性边界条件(CC)几乎能完全恢复真实信号，而使用非周期边界条件得到的结果和真实的仿真信号有很大的差别。

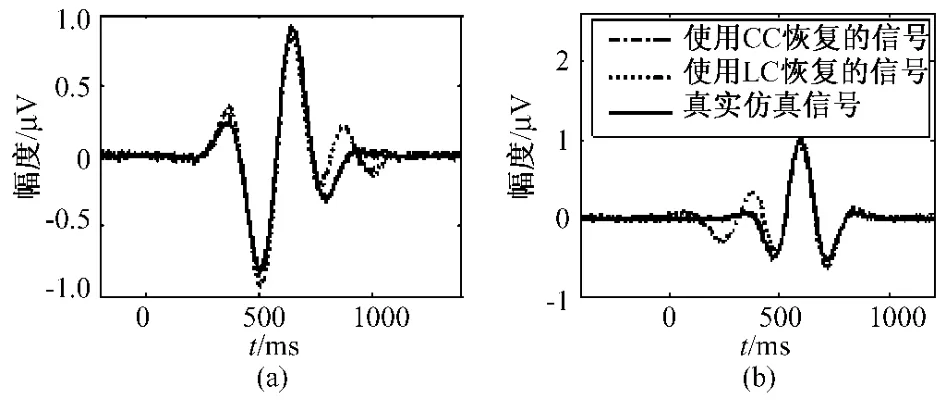
图3 两事件成分(刺激和反应)分解的仿真例子，CC表示循环卷积;LC表示线性卷积。(a)刺激事件对应的波形;(b)反应事件对应的波形Fig.3 Demonstration an illustrative of S-R decomposition.CC—circular convolution;LC—linear convolution;(a):waveforms corresponding to stimulus event;(b):waveforms corresponding to response event stimulus event

3.1.2 三事件成分的分解

不仿设3个事件分别为cue，stimulus，response，以cue出现的时间为参考时间，stimulus和response相对于cue时间的分布为高斯或均匀分布，其均值分别为250和300 ms，标准差都为100 ms，和两事件成分分解类似，使用两种边界条件在5种不同的信噪比条件下分别进行50次计算。α是0～2π 内的一个随机数，对于 fc，f，取 2.5～3 Hz的随机值，对于 fs，f取 3 ～4 Hz的随机值，对于 fr，f取3.5～4.5 Hz的随机值。结果如图4所示.

从图4中可以看出，和两事件成分分解结果非常类似，无论事件时间分布是高斯分布还是均匀分布，在5种不同的信噪比条件下，使用周期边界条件得到的分解结果比使用非周期边界条件得到的分解结果有更小的相对误差，有更大的相关系数(p＜0.001)，很明显在三事件成分分解算法中，使用周期边界条件也比非周期边界条件能得到更鲁棒的分解结果。图5显示了一个三事件成分分解的例子，其参数为SNR=1，对fc取f=2.66，γ=3，α=1.92，对 fs取 f=3.81，γ=2.5，α =2.33，对 fr取 f=3.96，γ=2，α=4.44.

3.1.3 事件时间分布对分解结果的影响

Zhang(1998)指出通常情况下只要事件时间有单峰分布，分解算法能得到很好的分解结果［10］。然而，事件时间的分布不一定具有单峰分布的特性，比如在研究视觉空间注意时使用的提示，基本上都是采用均匀分布。那么这里就产生了一个问题，是否事件时间的分布特性会影响分解算法的结果。在本节中，主要讨论关于事件时间分布的形状(高斯vs均匀)和分布的方差对分解结果的影响。由上两节的分析知道采用周期的边界条件要明显优于采用非周期边界条件，因此，本节中只考虑使用周期性的边界条件。相关的参数如下:SNR=0.33，对 fc取 f=3，γ=3，α =2/π，对 fs取 f=3.5，γ=2.5，α=π，对fr取f=4，γ=2，α=0.事件时间分布6种不同的标准差被分析，每种条件下50次计算。结果显示在图6中。

在图6中可以看到，随着事件时间分布标准差的增加，相对误差(RE)逐渐降低，相关系数(Cor)逐渐增加，这意味着大的事件时间分布标准差的分解结果比小的事件时间分布标准差的分解结果更为有效。同时统计结果显示高斯分布和均匀分布的结果没有显著性差异(P＞0.05)，这个结果说明分解结果不受事件时间分布的形状影响，而受到事件时间分布的标准差的影响，大的标准差能得到更好的分解效果。

图4 在不同的信噪比(SNR)以及不同边界条件下三事件成分分解算法计算得到的相对误差(RE)以及相关系数(Cor)，误差棒表示 RE或 Cor的标准差。(a)和(b)中事件时间分布为高斯分布，(c)和 (d)中事件时间分布为均匀分布Fig.4 The mean RE and Cor of three event related components decomposition using CC and LC under the difference SNR conditions，respectively，dot line:LC(linear convolution);solid line:CC (circular convolution).Error bar represented standard deviation of RE or Cor.(a)and(b):event time distribution is Gauss;(c)and(d):event time distribution is uniform

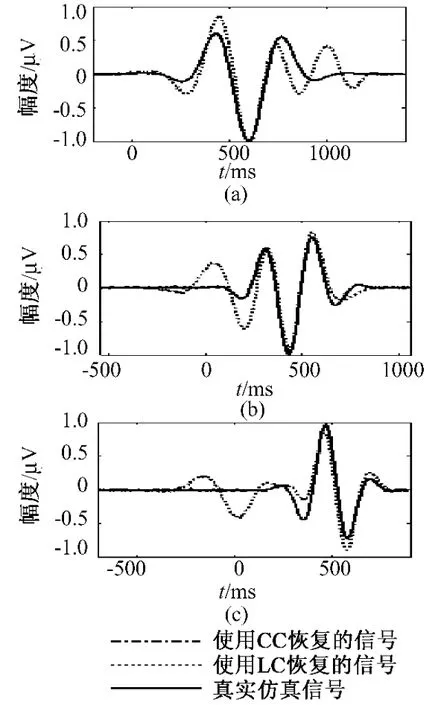
图5 使用两种不同边界条件下三事件成分(提示，刺激和反应)分解的仿真例子，CC表示循环卷积;LC表示线性卷积。(a)提示事件对应的波形;(b)刺激事件对应的波形;(c)反应事件对应的波形Fig.5 Demonstration an illustrative result of three components decomposition.CC—circular convolution;LC—linear convolution; (a): waveforms corresponding to Cue event;(b):waveforms corresponding toCueeventStimulusevent;(c)waveforms corresponding to Response event

3.2 真实实验数据结果

为了说明分解结果，首先仅选择一种条件的实验数据，‘cue’位于左视野，靶刺激位于左视野。选择其中的一个被试的PZ电极记录的数据，总共127次实验记录。数据采样率为250 Hz。分别按‘cue’、刺激、反应时间为事件参考能得到各自的迭加平均ERP(Fc，Fs和 Fr)。因为从仿真的结果知道采用周期边界条件的结果要明显好于采用非周期边界条件的结果，因此在计算中采用周期性的边界条件(CC)。

事件时间分布可以分别以不同的事件时间作为事件参考而得到，真实的事件相关的成分fc:提示成分(cue-component);fs:刺激成分(stimuluscomponent);fr:反应成分(response-component)分可以从式(14)中分别得到，结果显示在图7中。其次，对所有12个被试的PZ电极记录的数据分别进行三事件相关成分分解计算(采用周期性边界条件)，得到所有12个被试在 PZ电极上总平均 ERP(Fc，Fs和 Fr)以及总平均恢复出的事件相关成分(fc，fs和fr)。结果显示在图8中。从图8中可以看出对于‘Cue’成分，原始的叠加平均波形和恢复出的和‘Cue’相关的波形在时间段500～1 000 ms有较大差异;对于 stimulus’成分，原始的叠加平均波形和恢复出的和‘stimulus’相关的波形在时间段400～ 700 ms有较大差异;对于‘response’成分，原始的叠加平均波形和恢复出的和‘response’相关的波形在时间段0～200 ms有较大差异;表1是具体的统计结果。

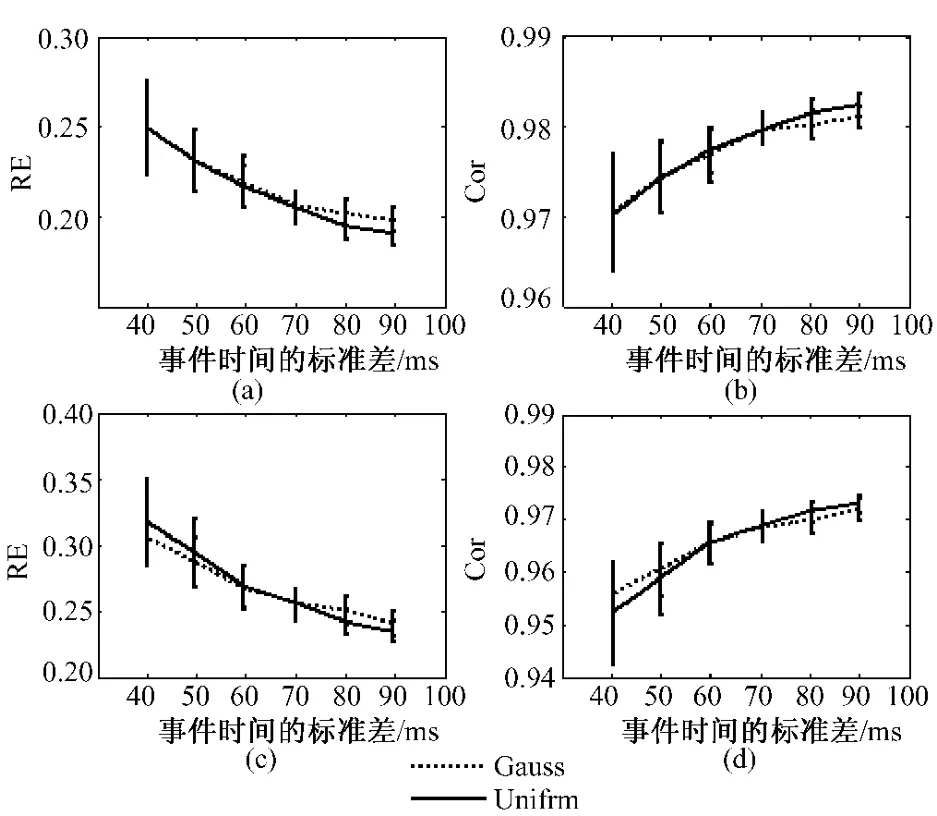
图6 不同事件时间分布条件下相对误差(RE)、相关系数(Cor)和事件时间分布(高斯分布 vs.均匀分布)的标准差之间的关系(周期边界条件)。(a):相对误差(RE)(两事件成分的分解);(b):相关系数(Cor)(两事件成分的分解);(c):相对误差(RE)(三事件成分的分解);(d):相关系数(Cor)(三事件成分的分解)。误差棒表示RE或Cor的标准差。Fig.6 The relationships between the RE，Cor and the standard deviation of difference event time distribution(Gauss vs.Uniform).(a):RE for two components decomposition;(b):Cor for two components decomposition;(c):RE for three components decomposition;(d):Cor for three components decomposition.Error bar represented standard deviation of RE or Cor

4 讨论

4.1 关于分解算法的讨论

4.1.1 扩展算法

两事件成分分解算法(S-R decomposition algorithm)是基于迭加平均ERP信号恢复真实的事件相关成分波形算法。但由于心理学实验设计过程中不可避免的有多于两个事件的参与，因此推广到三个或多个事件成分分解算法是有必要的。仿真结果显示(图3中的实线)两个或三个事件成分的分解算法能得到很好的效果。总的来说，无论参与的事件有多少个，算法的过程可以概括如下:以不同事件时间作为参考时间，采用周期性的边界条件(CC)可以得到以不同事件时间为参考的迭加平均ERP，同时计算任意一个事件时间相对于其余事件时间的分布，最终通过傅立叶变换或者时域矩阵方程(式(8)、(10)、(14)、(17)或式 (18)、(19))得到最终结果。

表1 原始叠加平均ERP波形和恢复事件相关波形在特定时间段上平均幅度的统计结果Tab.1 Result of statistic tests

4.1.2 边界条件

在计算以不同事件时间为参考的迭加平均ERP时，以及在对卷积进行计算的时候，由于信号长度有限，因此通常用周期性和补零的非周期性边界条件来处理，仿真的结果(图2和 图4)显示，边界条件的选取对分解结果有很大影响，采用周期性的边界条件明显好于采用非周期性边界条件，因此在实际计算中应该采用周期性的边界条件。

4.1.3 事件时间的分布

从图6的结果中可以看到，分解结果基本和事件时间分布的形状(高斯分布或均匀分布)无关而仅与事件时间分布的方差(标准差)有关。方差越大，分解的效果越好。考虑极端的情况，当事件时间分布趋于常数的时候，(w)将趋近于1，这种情况下不能完成分解。当然在实际情况中，事件时间分布有相对较大跨度(方差)的分布［10］，这使得能够应用分解算法得到真实的数据。

4.1.4 计算中的一些细节问题

在卷积计算中由于卷积核的截断可能引发波形失真，因此计算ERP的时间窗应该经可能的覆盖感兴趣的时间段。例如分段ERP数据的时候，应该尽可能的覆盖包含刺激开始的基线，以及最大反应的反应时后的一部分数据点，如果数据太短容易造成信号丢失现象。

另一方面，因为分解算法是基于平均ERP基础上进行的，而噪声总是存在于平均ERP中的，如果实验次数太少，势必导致平均ERP中噪声成分的增多，从而影响分解结果。非常明显，实验次数越多，ERP的信噪比就越高，分解的结果就越可靠。同时实验数据的预处理也是非常必要的，因为实验记录的EOG和 ECG等干扰成分将对分解结果造成影响。

图7 在PZ电极上直接迭加平均得到的 ERP(Fc，Fs和Fr)和恢复出的事件相关成分(fc，fs和 fr)。(a)以刺激时间为参考，cue时间和反应时间的分布。刺激开始时间是0 ms;(b)恢复出的cue成分(fc)波形和直接按cue时间迭加平均的波形(Fc)，cue出现的时间是0 ms;(c)恢复出的刺激成分(fs)波形和直接按刺激时间迭加平均的波形(Fs)，刺激出现的时间是0 ms;(d)恢复出的反应成分(fr)波形和直接按反应时间迭加平均的波形(Fr)，反应出现的时间是0 msFig.7 Recovery of cue-and stimulus-and responsecomponent waveforms at electrode PZ，denoted as fc，fsand frrespectively，the cue-aligned，stimulus-aligned and response-aligned ERP denoted as Fc，Fsand Frrespectively.(a)Event time distribution are given reference to stimulus onset，stimulus onset at 0 ms;(b)recovered the cue-component waveform and cue-aligned ERP waveform，cue onset at 0 ms;(c)recovered the stimulus-componentwaveform and stimulus-aligned ERP waveform，stimulus onset at 0 ms;(d)recovered the response-component waveform and response-aligned ERP waveform，response onset at 0 ms

4.2 关于实验数据的讨论

从图7和图8可以看到，重建的cue-component fc，stimulus-component fs和 response-component fr波形和直接按不同事件时间迭加平均的波形(Fc，Fs和Fr)有很大的不同，其原因是真实的事件相关成分在迭加的过程中相互窜扰。在这里也为三事件成分的假设提供了一个证据，因为在每次试验中得到的实验数据，事实上由不同事件引发的事件相关成分波形的一个线性迭加结果。

4.2.1 Fc与fc

在图7(b)以及图8中的‘Cue’，可发现一个很明显的现象，cue-component fc和按 cue时间迭加平均波形cue-aligned Fc，在300 ms以前的部分波形幅度大致是一致的，在500～1 000 ms之间却有很大的差异，其中fc在500～1000 ms之间几乎接近基线而Fc明显存在一个偏离基线的成分，从表1中的统计结果也可以看出，fc在500～1 000 ms之间的平均幅度为0.20 μV，几乎接近基线而Fc在这个时间段的平均幅度为2.13μV，明显地偏了离基线水平。按照视觉处理的神经机制，当‘cue’出现后大约500 ms内大脑将处理‘cue’信号，500 ms后将转换到处理刺激事件和反应事件，因此大约500 ms后的阶段大脑对‘cue’信号的处理基本完毕，此时相对于‘cue’作为时间参考而言，信号应该回到基线的水平，因此恢复出的cue-component fc能真实的反应出大脑对‘cue’的处理过程，而按‘cue’时间的直接迭加平均信号 cue-aligned Fc对于500～1000 ms内的信号很难解释，很明显这是因为Fc中交叉窜扰了刺激成分信号fs和反应成分信号fr，因此直接迭加平均ERP会影响对 ERP成分的解释。同时发现，因为‘cue’开始 500 ms后 cue-component fc基本回到基线水平，假如选择 SOA ＞500 ms，cue-component fc将不会影响到刺激迭加平均信号或反应迭加平均信号，这有助于心理学实验的设计。

4.2.2 Fs与fs

在图7(c)中，Fs和 fs的主要差异在刺激开始后 300～800 ms，对总平均数据而言，Fs和 fs的主要差异在刺激开始后 400～700ms(图 8中‘Stimulus’)，这段事件内 Fs的幅度明显大于 fs的幅度。由于平均反应时为(300±100)ms(总平均反应时(288±120)ms)，而刺激引起的P3成分的出现在刺激呈现后的大约300～500 ms，这使得刺激迭加平均波形Fs中交叉窜扰了反应成分信号fr，从而导致直接迭加平均信号Fs相对于恢复出的fs在时间段400～700 ms有较大幅度。

4.2.3 Fr与fr

图8 所有12个被试在 PZ电极上总平均ERP(Fc，Fs和Fr)以及总平均恢复出的事件相关成分(fc，fs和 fr)。(a)恢复出的cue成分(fc)波形和直接按 cue时间迭加平均的波形(Fc)，cue出现的时间是0 ms;(b)恢复出的刺激成分(fs)波形和直接按刺激时间迭加平均的波形(Fs)，刺激出现的时间是0 ms;(c)恢复出的反应成分(fr)波形和直接按反应时间迭加平均的波形(Fr)，反应出现的时间是0 msFig.8 Recoveryof cue-and stimulus-and responsecomponentwaveforms atelectrode PZ for all12 subjects，denoted as fc，fsand frrespectively，the cuealigned，stimulus-aligned and response-aligned ERP denoted as Fc，Fsand Frrespectively.(a)recovered the cue-component waveform and cue-aligned ERP waveform，cueonset at 0ms;(b)recoveredthe stimulus-component waveform and stimulus-aligned ERP waveform，stimulus onset at 0 ms;(c)recovered the response-component waveform and response-aligned ERP waveform，response onset at 0 ms

在图7(d)和图8中的‘Response’中，Fr和 fr的主要差异在反应开始后 0～200 ms，这段事件内Fr的幅度明显大于fr的幅度。这种差异的主要原因和上一节类似，同时，因为选择的电极位于大脑后顶叶，这个区域既是P3的产生区域，同时这个区域靠近与运动相关脑区，同时由于按键反应是一个运动过程，大脑的体传导导致了运动相关的成分和刺激相关的成分的交叠，而直接迭加平均波形不能反映这样的情况。

4.3 应用

因为事件成分分解算法能恢复出真实的事件相关成分，有助于更好地分析和理解一些心理学问题的神经机制，例如在研究返回抑制(IOR(inhibition of return))的神经机制以及响应抑制等问题的时候，由于总体的迭加平均ERP存在交叉串扰，造成了对此类问题认识的一些争议，所以此分解方法的应用有可能带来对这些问题更为深入的认识。

5 结论

通过对事件相关成分分解算法的理论研究和仿真计算，发现边界条件的选取直接影响到计算效果的好坏，采用周期性的边界条件明显好于采用非周期性的边界条件。同时由于事件时间的分布也影响分解结果，为此本仿真研究表明事件时间的分布形状(高斯分布和均匀分布)不会影响分解结果，但事件时间分布的方差(标准差)对分解结果有较大影响，方差越大分解效果越好。应用多事件成分分解算法到真实的实验数据中，结果能很好的吻合心理学过程，并为心理学实验的设计提供了新的参考。

(致谢:特别感谢 尧德中教授，张俊教授以及田银博士对本研究工作的帮助)。

［1］Squires NK，Squires KC，Hillyard SA.Two varieties of longlatency positive waves evoked by unpredictable auditory stimuli in man ［J］.Electroenceph Clin Neurophysiol，1975，38(4):387-401.

［2］Hillyard SA，Picton TW.Electrophysiology of congition［M］.Maryland:American Physiological Society，1987.519-584.

［3］KutasM，Hillyard SA.Event-related brain potentials to semanticallyinappropriate and surprisingly large words［J］.Biol Psychol，1980，11(2):99-116.

［4］Gehring WJ，Goss B，Coles MGH，et al.A neural system for error detection and compensation ［J］.Psycholog Sci，1993，4:385-390.

［5］Falkenstein M，Koshlykova NA，Kiroi VN，et al.Late ERP components in visualand auditory go/nogo tasks ［J］.Electroenceph Clin Neurophysiol，1995，96(1):36-43.

［6］Simson R，Vaughan HG，Ritter W.The scalp topography of potentials in auditory and visual go/nogo tasks［J］.Electroenceph Clin Neurophysiol，1977，43(6):864-875.

［7］Kok A.Effects of degradation of visual stimulation on components of the event-related potential(ERP)in go/nogo reaction tasks［J］.Biol Psychol，1986，23(1):21-38.

［8］Coles MGH.Modern mind-brain reading:Psychophysiology，physiology and cognition ［J］.Psychophysiol，1989，26(3):251-269.

［9］Zhang Jun.Decomposing stimulus and response component waveforms in ERP ［J］.Journal of Neuroscience Methods，1998，80(1):49-63.

［10］Yin Gang，Zhang Jun，Tian Yin，et al.A multi-component decomposition algorithm for event-related potentials［J］.Journal of Neuroscience Methods，2009，178(1):219-227.

［11］Yao Dezhong.A method to standardize a reference of scalp EEG recording to a point at infinity［J］.Physiol Meas，2001，22(4):693-711.

A Study of Event Related Components Decomposition Algorithm for Event-Related Potentials

YIN Gang LIU Tie-Jun*
(School of Life Science and Technology，University of Electronic Science and Technology of China，Chengdu 610054，China)

Q81;R338

A

0258-8021(2010)03-0363-10

10.3969/j.issn.0258-8021.2010.03.008

2009-11-20，

2010-02-22

国家自然科学基金资助项目(60736029);国家高技术研究发展(863)计划(2009AA02Z301)

*通讯作者。 E-mail:liutiejun@uestc.edu.cn