数字图像相关测量钢绞线的弹性模量❋

张 蕊,贺玲凤

(华南理工大学土木与交通学院,广东 广州 510640)

0 引 言

钢绞线广泛应用于预应力结构中,如铁路桥梁、公路桥梁、房屋建筑等,弹性模量是钢绞线的一个重要参数,因此对其准确测量具有重要意义.传统的测量方法有：①应变片法.大量的粘贴非常繁琐和耗时.由于钢绞线是由外层钢丝螺旋状紧包中心钢绞线扭结而成,应变片只能在顺着外层钢丝方向上粘贴,故实际测得的是沿着钢绞线的斜向应变,且采样点有限.②机械式引伸计法.在试样上安装引伸计,在线性阶段读取拉力机表盘和引伸计的若干数据,计算出弹性模量.这种方法测量单筋的弹性模量简单准确,但是用来测量钢绞线的弹性模量,由于其在拉伸过程中股中单丝的摩擦产生扭转、振动等,这就影响了测量质量.

数字图像相关(Digital Image Correlation,DIC)方法作为一种非接触、全场、无损光学测量方法,已被成功地应用于科学研究和工程实际中的许多领域[1-5],具有如下突出优点：① 对环境噪音不敏感.②可获得全场变形信息,与应变片法相比,操作简便.③ 非接触测量.可以测量到传统方法无法测量的部位.鉴于此,本文用 DIC方法测量了钢绞线的弹性模量.首先,对采集到的序列数字图像将第一幅作为参考图像,将不同载荷下的数字图像均与第一幅数字图像作相关运算,由此测量了钢绞线的全场位移;然后,用线性平面拟合已得到的位移场,得到样本测量范围内的平均应变;最后,用最小二乘线性回归拟合应力-应变曲线,从而确定钢绞线的弹性模量,并与传统的机械式引伸计测试结果比较,吻合较好.

1 数字图像相关的基本原理

数字图像相关方法[6]是先进的光电技术,数字图像处理技术及数值分析相结合的产物;以数字图像相关来测量物体在一定载荷作用下的位移与应变;用 CCD采集不同载荷下的图片;以数字图像相关方法处理变形前后被测物体表面随机分布的人工或自然散斑场的灰度信息,通常将变形前的数字图像称为“参考图像”,变形后的数字图像称为“变形后图像”,其基本原理如图 1所示.在参考图像中取以某待求点 P(x0,y0)为中心的(2M+1)×(2M+1)pixels大小的矩形参考图像子区,在变形后图像中通过一定的搜索方法按选定的相关函数来进行相关计算,获得相关系数取最小值的以 P′(x′0,y′0)为中心的目标图像子区.在利用数字图像进行实际计算时,通常将参考图像中的待计算区域划分成虚拟网格形式,通过计算每个网格节点的位移以得到全场的位移信息.相邻网格点之间的距离为计算步长.Tong[7]推荐使用标准化协方差相关函数

式中：f(x,y)是参考图像子区中坐标为(x,y)点的灰度;g(x′,y′)是目标图像子区中对应点(x′,y′)的灰度;fm,gm分别为参考图像和目标图像子区灰度的平均值.变形后坐标(x′,y′)与变形前坐标的关系如式(2).

式中：u,v分别为参考图像子区中心点在 x,y方向的位移;Δx,Δy为点 Q到子区中心点 P的位移.变形后图像子区如图 1所示.参考图像中的 P,Q点分别对应于变形后图像中的 P′,Q′点.Q′(x′,y′)点的表达式如式(2).

p包含 6个参数 u,ux,uy,v,vx,vy,当变形前后图像子区最为相似的时候,相关系数C(p)应取最小值.用 New ton-Raphson偏微分修正法和 Hessian矩阵优化 C(p)求得 C(p)的最小值,进而得到该图像子区中心点 P(x0,y0)的位移 u,v及导数 ux,uy,vx,vy;然后图像子区沿 x轴移动到下一图像子区,移动的像素数称为步长.计算出第2点 P(x1,y0)的位移,通过全场计算算出全场位移.在 N-R方法的实现中,为使相关系数的一阶和二阶导数在搜索区域内存在且连续,用双三次样条差值进行迭代处理.

图1 变形前后图像子区示意图Fig. 1 Schematic diag ram of refere nce and ta rg et( o r defo rmed) subsets

2 应变算法

在获得全场面内位移场分布后,传统的应变计算可以通过差分法获得[8],然而数值差分会放大位移场的噪声,微小的位移误差会导致较大的应变误差[9].考虑本次试验均匀拉伸样本,所以由 DIC算出的全场位移可拟合为平面.拟合的过程即包含了对位移场的平滑去噪.为了计算整个计算区域内的平均应变,对整个计算区域的位移场用方程(3)进行线性平面拟合.

式中：x,y为位移场中各数据点的坐标(以像素为单位).得到拟合多项式的系数 a0,…,b2后,计算区域内的平均应变按式(4)计算

由于拟合的过程即包含了噪声的去处,因此应变测量精度有所提高.

3 实验过程及结果

实验装置如图 2所示.CCD安放在三脚架上,其光轴垂直钢绞线轴线,并准确对其聚焦成像.光源可使用普通光源或冷光源.本实验中由于背景光较明亮,未使用特别光源.钢绞线的表面呈黑色,为给相关匹配提供特征,试样表面经过简单擦试,以形成随机分布的人工散斑模式.钢绞线公称直径为15.24 mm,强度级别为 1860 MPa,公称面积为 140 mm2.实验时钢绞线两端由试验机夹持.为了考察DIC方法的可靠性,在钢绞线中间段安装了引伸计,标距为 385 mm,由百分表测量标距内的变形.以40kN作为测试弹性模量的初始荷载,然后以等荷载增量的方式加载,荷载增量为 20kN.即在 F=40kN,60kN,…,160kN各级荷载下分别采集钢绞线的数字图像和读取百分表的数据.正式采集数据和图像前对钢绞线进行了预加载.

图2 数字图像相关原理图Fig.2 Schematic diagram of digital image correlation

图3 拍摄不同载荷下物体表面数字图像Fig.3 Digital images of the sample surface under different loads

本研究共对 3根钢绞线进行了试验,第1根钢绞线只测试了 1次,第2根和第3根试样分别测试了2次.即从 40kN起,以 20kN的增量逐步加载至 160kN,采集各级荷载下的数字图像和读取百分表的数据,然后卸载至 20kN,重复上述测试过程.

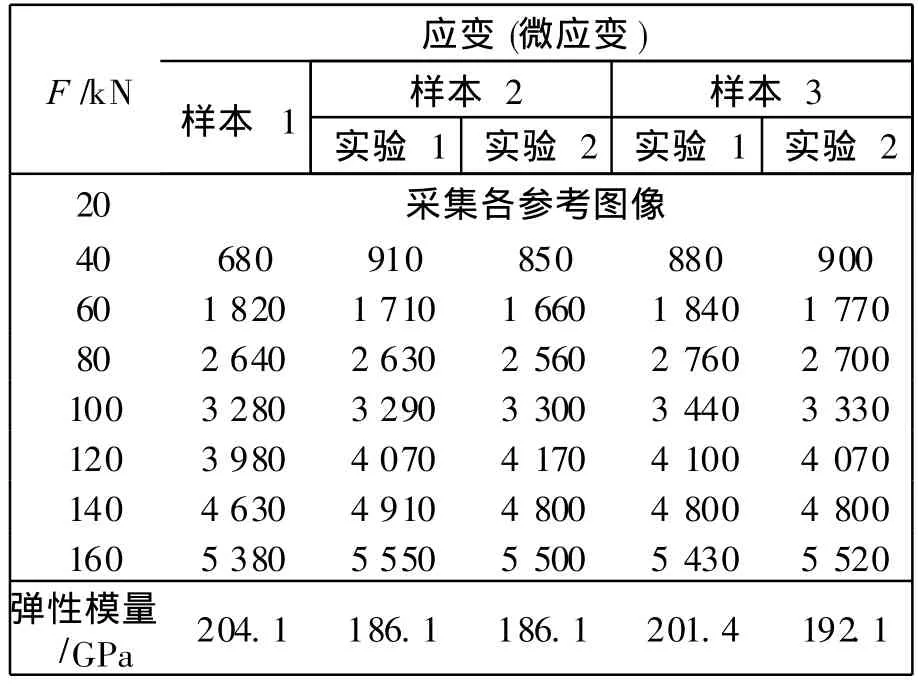
表1 用 DIC方法所得应变值Tab.1 Strain obtained from DIC method

图4 第1根钢绞线不同载荷下 V场位移的演化Fig.4 The V displacement fields distribution of the first strand wire under different loads

所采数字图像如图 3所示,分别为第1个试样在轴向荷载为 20kN,40kN,60kN时采集的数字图像.用第1节所述方法对变形前后两幅图像进行相关运算(各级载荷下的数字图像分别与第1幅数字图像进行相关运算),计算区域如图框内所示,图像子区大小为 61,步长为 10,求得全场位移.图4为 DIC计算结果,其具体数值见表 1.表 2为引伸计测试的原始数据.

图53根钢绞线应力-应变曲线Fig.5 Stress-strain curves of the three strand wires

4 试验结果分析

由 DIC方法所得钢绞线弹性模量的均值为 193.96 GPa,标准差为 8 GPa;由引伸计所得的均值为198.8 GPa,标准差为 6 GPa.DIC测量得到的标准差与机械式引伸计测量得到的均值、标准差相近,由此可见,二者吻合较好.Dowling[10]提议试验中用标准差系数评价弹性模量,即标准差与均值的比值约为 0.05;而 DIC方法测量结果的标准差系数为 0.04,小于 0.05.这也证实了 DIC方法的有效性,同时表明了 DIC方法的可重复性较好.由图 4可见,7幅图像的 V场位移整体趋势一致,正如所期望的由下至上位移逐渐增大,这是由于钢绞线上端加载受拉所致.值得注意的是,图 4(b)～(g)这 6幅 V场位移分布模式趋于一致,而相比之下(a)图位移场分布显得杂乱,中间部分位移排列没有清晰的顺序.因此,本文在应力-应变拟合时去掉第1点即(a)图.由于镜头畸变对图像边缘的影响较大,因此在计算时尽量选择了图像中间的区域.如图 3所示,计算区域避开了上下边缘.同时,由于 DIC方法的测量范围与引伸计的测量范围与测量位置不同,也导致了两者测量结果存在一定差异.由 DIC测试结果可见,同一样本在同一载荷下两次测得的应变并不完全一致,最大相差 110微应变,这是由于 DIC算法的随机误差所致.在等载荷加载的条件下,DIC测得的应变增量并不完全一致,同样是由于 DIC算法的随机误差所致,而引伸计法同样也存在测量误差导致的变形增量不完全一致性.

5 结 论

本文利用非接触式数字图像相关方法这一基于数字图像处理和数值计算的先进全场变形光学测量技术对钢绞线的弹性模量进行了测试,为考察 DIC方法测试结果的可靠性,与传统接触式引伸计测量方法进行了对比,二者吻合较好,但二者的应变误差的比较以及产生的原因仍需作进一步研究.总之,本文研究结果显示：DIC可用于工程中钢绞线弹性模量的测量.

[1]赵清澄.光测力学教程[M].北京：高等教育出版社,1996.

[2]潘兵,谢惠民,续伯钦,等.应用数字图像相关方法测量缺陷试样的全场变形[J].实验力学 ,2007,22(3-40)：379-384.Pan Bin,Xie Huimin,Xu Boqin,et al.Full-field deformation measurement of specimen with discontinuity using digital image correlation[J].Experimental Mechanics,2007,22(3-40)：379-384.(in Chinese)

[3]Huang Y H.Optical strain gauge vs.traditional strain gauges for concrete elasticity modulus determination[J].Optik-International Journal for Light and Electron Optics,2009,120(3)：2.

[4]Pan B,Xie H M,Hua T,et al.Measurement of coefficient of thermal expansion of films using digital image correlation method[J].Polymer Testing,2009,28：75-83.

[5]Sutton M A,Turner J L,Bruck H A,et al.Full-field representation of discretely sampled surface deformation for displacement and strain analysis[J].Exp.Mech.,1991,31(2)：168-77.

[6]Peters W H,Ranson W F.Digital imaging techniques in experimental stress analysis[J].Opt.Eng.,1982,21(3)：427-431.

[7]Tong W.An evaluation of digital image correlation criteria for strain mapping applicant[J].Strain,2005,41(4)：167-175.

[8]Zhang Dongsheng,Luo Miao,Arola D.Displacement/Strain measurements using an optical microscope and digital image corelation[J].Optical Engineering,2006,45(3)：33605.

[9]Pan B,Asundi A,Xie H M,et al.Digital image correlation using iterative least squares and pointwise least squares for displacement field and strain field measurements[J].Optics and Lasers in Engineering,2009,47(7-8)：865-874.

[10]Dowling N E.Mechanical Behavior of Materials[M].2nd ed.Prentice Hall,1998.