应用人工神经网络方法预测气井积液

栾国华何顺利舒绍屹胡景宏王晓梅

（1.中国石油大学石油工程教育部重点实验室,北京 102249；2.中国石油工程设计有限公司西南分公司,四川 成都 610017；3.中国地质大学能源学院,北京 100083；4.四川省泸州市龙马潭区碳黑厂井下作业公司,四川 泸州 646000）

应用人工神经网络方法预测气井积液

栾国华1何顺利1舒绍屹2胡景宏3王晓梅4

（1.中国石油大学石油工程教育部重点实验室,北京 102249；2.中国石油工程设计有限公司西南分公司,四川 成都 610017；3.中国地质大学能源学院,北京 100083；4.四川省泸州市龙马潭区碳黑厂井下作业公司,四川 泸州 646000）

气井井筒积液对天然气的开采影响极大，准确地计算气井临界流量对气井开发至关重要。气井携液临界流量理论计算模型主要有液滴模型和携液率模型，然而在实际计算过程中往往会出现计算结果偏差大、不能满足工程需要等问题。文中提出一种应用人工神经网络方法预测井筒积液的新模型，该模型充分利用了气井现有的生产测试数据，简化了大量复杂的机理研究，具有更广泛的实用性。生产井的计算结果表明，应用神经网络模型预测气井积液的成功率较高，可以用来判断气井积液。

神经网络；气井积液；液滴模型；持液率模型

1 气井携液模型

1.1 液滴模型

气井开始积液时，井筒内气体的最低流速称为气井携液临界流速，对应的流量称为气井携液临界流量。Turner在假设被高速气流携带的液滴是圆球形的前提下，导出了气井携液临界流量和产量计算公式，该模型适用于气液比非常高（GLR＞1 400）、流态为雾状流的产液气井［1］。其他各种高气液比的临界携液模型都是基于高速气流携带液滴的理论基础，将液滴的形状加以修正并重新界定气体曳力系数的 “椭球液滴模型”、“球帽形液滴模型”［2-5］。Turner液滴模型假设，排出气井积液所需的最低条件是使气流中的最大液滴能连续向上运动。根据最大液滴受力情况确定气井携液临界

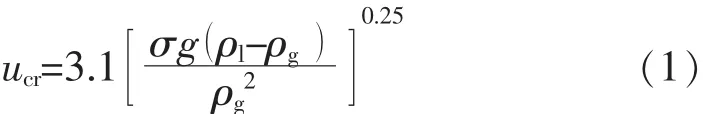
式中：ucr为气井携液临界流速，m·s-1；ρl为液体密度，kg·m-3；ρg为气体密度，kg·m-3；σ为气、液之间的界面张力，N·m-1；g为重力加速度，m·s-2。

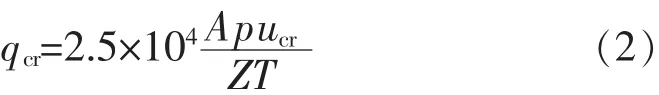
气井携液临界流量为流速，即气体对液滴的曳力等于液滴的沉降重力。因此，利用Turner液滴模型计算得到携液临界流速为

式中：qcr为气井携液临界流量，104m3·d-1；A为油管横截面积，m2；p为压力，MPa；T为温度，K；Z为气体偏差因子。

Turner的圆球液滴模型携液公式计算出的临界流速和最小携液产量相对较高；椭球液滴的有效迎流面积大，容易被天然气带出地面，由椭球液滴模型计算出的临界流速和最小携液产量相对圆球模型小得多；球帽液滴模型应用了最新的流体力学的成果，认为液滴呈球帽形的可能性最大，该模型的受力面积较李闽模型更大，计算出更小的临界流速和最小携液产量。

1.2 携液率模型

当井筒内气液比低于1 400时，井筒内流动的不再是雾状流体，不能采用液滴模型方法计算。文献［6］经过大量现场试验,得到了适用于低气液比气井两相流的压降预测关系式，即Hagedorn-Brown方法。

低气液比气井携液临界流量的确定原则为：利用Hagedorn-Brown计算井筒各段的理论持液率、实际持液率，如果各段的理论持液率都大于实际持液率，则气井在该产气量条件下能够正常携液生产；当理论持液率都小于实际持液率时，气井携液困难并开始积液，通过改变气井产气量找出气井正常携液的最小产气量，就是低气液比的携液临界流量［7］。

2 气井积液预测BP神经网络模型

2.1 人工神经网络基本原理

人工神经网络是近年来非常流行的一种系统建模方法，特别是其对非线性系统具有良好的逼进能力，以及并行性、容错性、自学习和自适应等性质，使其在系统建模、控制、信号处理、模式识别中得到广泛应用。

在众多类别的神经网络中，BP神经网络，也称误差反向传播神经网络，是一种能从样本集中有效地学习判别函数的系统。本文选用三层BP神经网络方法来设计构造气井井筒积液预测分类器［8-9］。

2.2 样本准备及参数预处理

选择气井实测生产数据为训练样本，其中输入参数有：产层深度、井口压力、产气量、产油量、产水量、气体相对密度、凝析油相对密度、油管尺寸、套管尺寸；输出参数是气井真实的生产状态，为实现神经网络数值计算，可把气井生产状态抽象为数值，“1”代表井底有积液，“0”代表井底无积液［10］。为避免由于样本过少可能导致网络外推能力不够，以及样本过多增加网络的训练负担，BP神经网络训练采用“交叉验证”方法，将所有样本分为训练样本、验证样本或测试样本。

由于不同气井的测试数据的精度和量纲可能不一致，在进行分类前，需对数据进行预处理；当各分量的物理意义相同且为同一量纲时，应在整个数据范围内确定最大值xmax和最小值xmin，进行统一变换处理。将输入输出数据变换为［0，1］区间的值常用以下变换式：

式中：xi为输入或输出数据；xmin为数据变化范围的最小值；xmax为数据变化范围的最大值。

2.3 神经网络结构设计

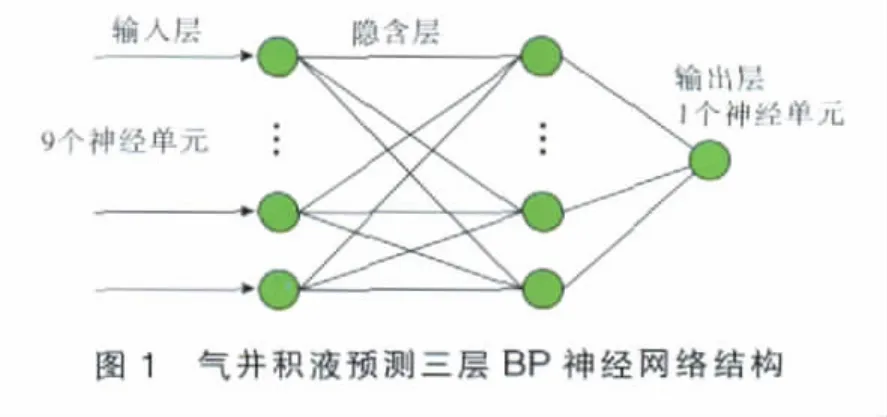
据上文所述，设计得到神经网络的输入层神经元数目个数为9，输出层为1。隐含层神经元数目与网络模型的好坏有直接关系，然而隐含层神经元数目选择不存在理想的解析式，往往需要根据设计者的经验和多次实验来确定。本文选用的最佳隐含层神经元数目nim的参考公式为：nim=(n+m)/2+a，其中m为输出单元神经元数，n为输入单元数，a为1～10的常数。最后得到气井积液预测三层BP神经网络结构（见图1）。

2.4 数据训练及学习

利用BP神经网络对归一化的输入样本进行学习与训练，BP网络的训练学习是一种有监督的学习，要求每一个输入模式矢量与表示所期望的输出模式矢量必须配对。一般来说，网络输出值yiactual与期望输出值yiexpect是不相等的。对于每一个输入的模式样本，其均方误差为Ek：

对于所有p个学习样本，网络的均方误差为E：

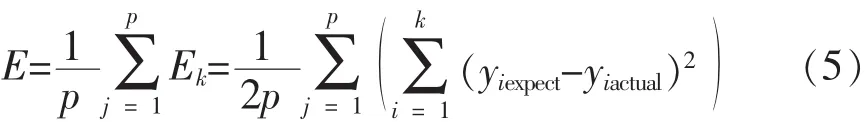
训练学习过程由2部分组成：1）网络内部的前向计算，2）误差的反向传播计算。其主要目的就是通过逐步调整网络的内部连接权按均方误差减小的方向进行，以达到指定的要求。网络内部连接权值是采用推广的规则完成的。采用MATLAB的神经网络工具箱进行编程计算，神经网络训练框图见图2。

由于神经网络输入和输出之间存在着非线性关系，在计算气井临界流量时采用试凑法。

计算原则为：1）设置相应的产气量为固定步长；2）假如判断气井为积液状态，则逐步增加当前产气量，然后重新归一化计算，直到判断结果为不积液为止，气井不积液时情况相反。

3 实例分析

选取具有代表性的某气田实测数据300组，归一化处理得到BP神经网络的训练样本参数200组、验证样本参数100组、测试样本参数15组（见表1）。

分别应用BP神经网络模型、理论计算模型(Turner模型+持液率模型)对测试样本进行计算，计算得到的临界流量结果见表2。

如表2所示，当气井处在临界积液状态时，即计算得到的携液临界流量与实际的产气量相接近时，应用理论模型对气井生产状态进行判断则会出现误差，相比之下，神经网络方法能够较好地判断气井是否处在临界积液状态下。

对于已经积液的气井或者远离积液危险的气井而言，理论模型的计算结果与神经网络模型的计算结果之间的差值很小，都能够用来对气井的生产状态进行判断。实际应用结果表明，神经网络模型具有广泛的适用性。

通过上述分析，可知理论模型适用于处在完全积液状态或完全无积液状态的生产气井；神经网络模型可用于任何条件下的气井生产状况的判断，并有较高的预测精度；在进行实际气井生产状态判断时，可以结合采用2种方法，采用相互验证、相互检验的方法，使得判断结果更加准确。

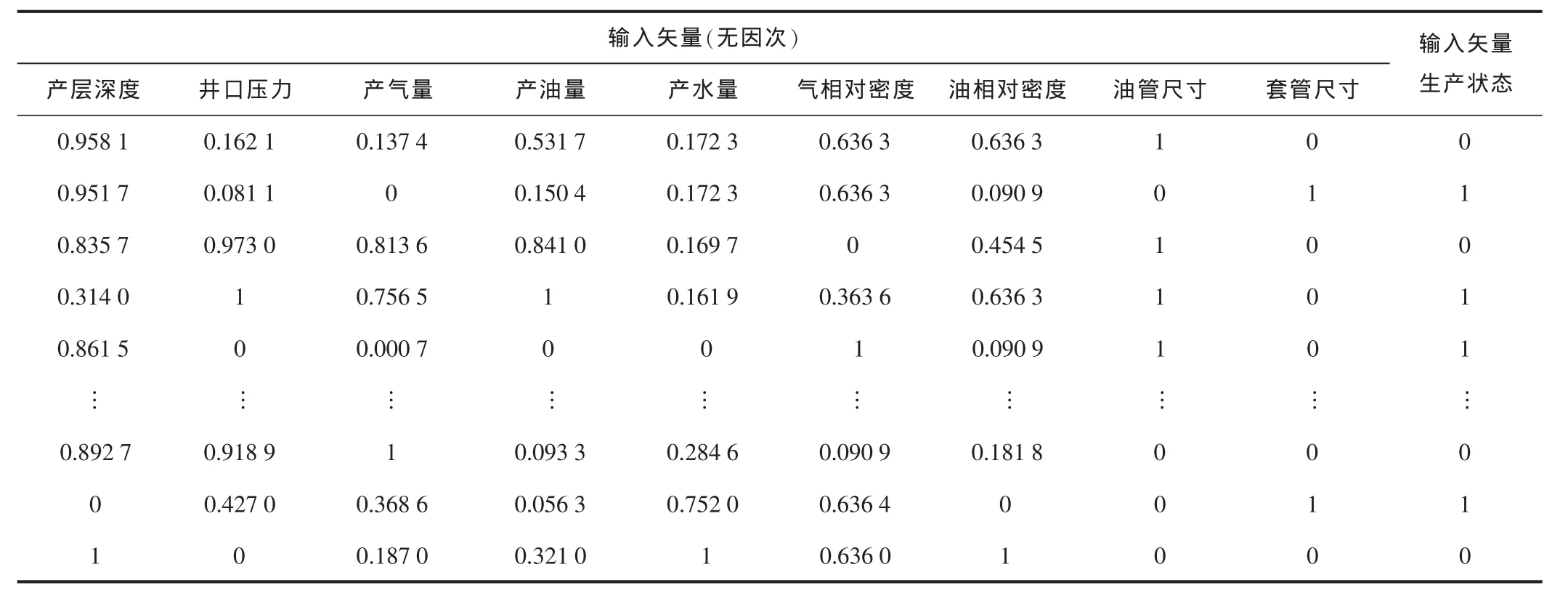
表1 归一化的BP神经网络训练、验证样本参数

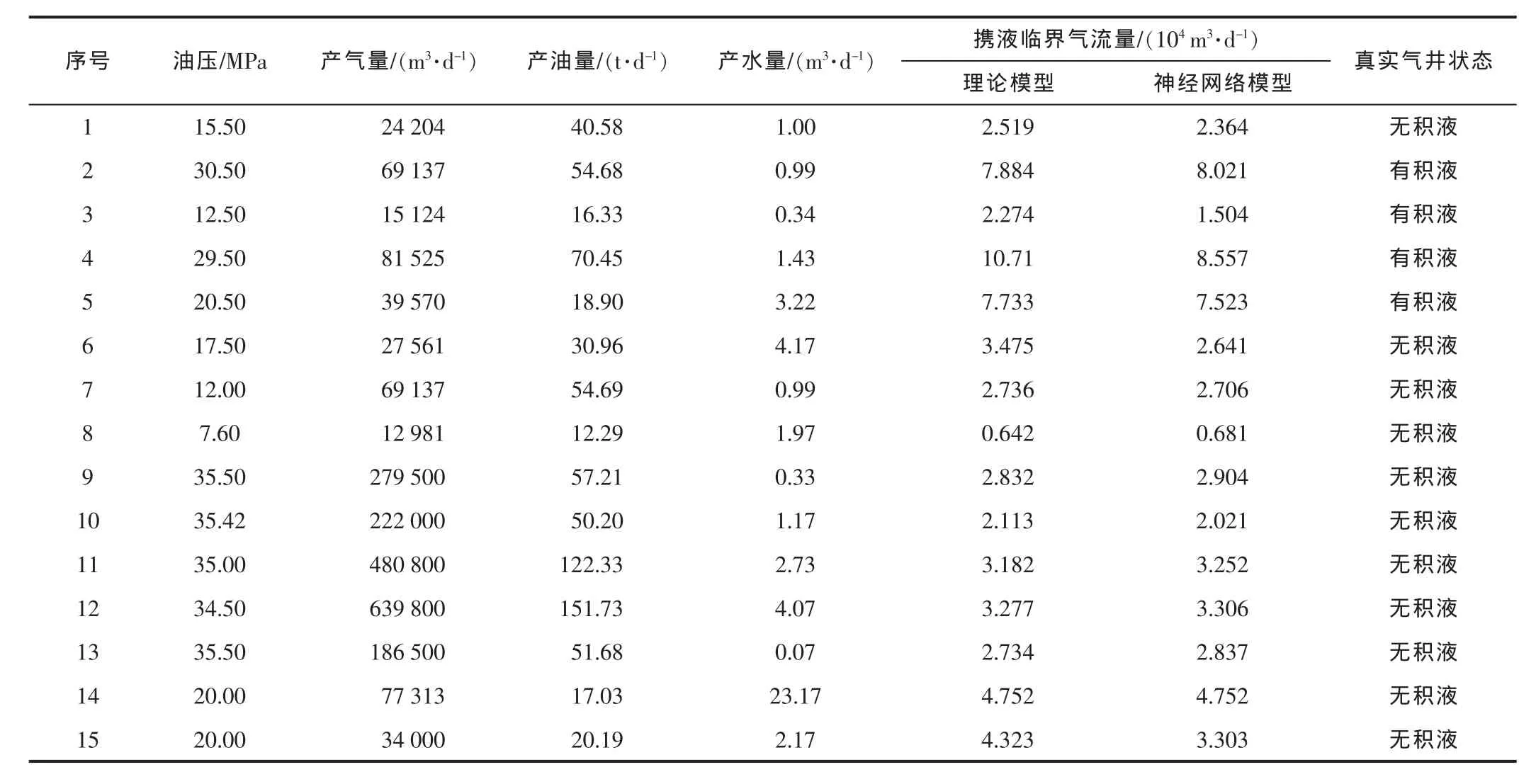
表2 2种模型计算结果对比

4 结论

1）总结了气井井筒积液的几种判断方法，着重分析了气井积液预判理论计算模型，给出了液滴模型的适用范围及使用效果。

2）提出应用人工神经网络方法预测气井井底积液的新方法，建立了气井井筒积液预测的BP神经网络模型，并给出具体的设计步骤。

3）应用BP神经网络模型对实际生产气井进行积液预测，得到的预测精度较高。

［1］ Turner R G，Hubbard M G，Dukler A E.Analysis and prediction of minimum flow rate for the continuous removeal of liquids from gas wells［J］.JPT，1969，21（11）：1475-1482.

［2］ Coleman S B，Clay H B，McCurdy D G，et al.A new look at predicting gas-well load-up［J］.JPT，1991，43（3）：329-333.

［3］ Li M，Li S L，Sun L T.New view on continuous-removal liquids from gas wells［A］.SPE 75455，2001.

［4］ 李闽，郭平，谭光天.气井携液新观点［J］.石油勘探与开发，2001，28（5）：105-106.

Li Min，Guo Ping，Tan Guangtian.New look on removing liquids from gas wells［J］.Petroleum Exploration and Development，2001，28（5）：105-106.

［5］ 王毅忠，刘庆文.计算气井最小携液临界流量的新方法［J］.大庆石油地质与开发开发，2007，26（6）：82-85.

WangYizhong，Liu Qingwen.A new method tocalculatethe minimum critical liquids carrying flow rate for gas wells［J］. Petroleum Geology& Oilfield Development in Daqing，2007，26（6）：82-85.

［6］ 李安，万邦烈，楼浩良.铅直气井两相管流研究现状综述［J］.石油钻采工艺，2000，22（4）：45-47.

Li An，Wan Banglie，Lou Haoliang.A Summary of present studies on gas liquid two-phase flow in vertical tubes［J］.Oil Drilling and Production Technology，2000，22（4）：45-47.

［7］ 吴志均，何顺利.低气液比携液临界流量的确定方法［J］.石油勘探与开发，2004，31（4）：108-111.

Wu Zhijun，He Shunli.Determination of the critical liquid carrying flow rate at low gas liquid ratio［J］.Petroleum Exploration and Development，2004，31（4）：108-111.

［8］ 张德丰.MATLAB神经网络应用设计［M］.北京：机械工业出版社，2009.

Zhang Defeng.MATLAB neural network application design［M］. Beijing：China Machine Press，2009.

［9］ 张际先.神经网络及其在工程中的应用［M］.北京:机械工业出版社，1996.

Zhang Jixian.Neural network and its application in engineering［M］.Beijing：China Machine Press，1996.

［10］Sayed E A.Prediction ofcritical gas flow rate for gas wells unloading［A］.SPE 78568，2002.

Using artificial neural network method to predict liquid loading in gas well

Luan Guohua1He Shunli1Shu Shaoyi2Hu Jinghong3Wang Xiaomei4
(1.MOE Key Laboratory for Petroleum Engineering in China University of Petroleum,Beijing 102249,China;2.Southwest Company,China Petroleum Engineering Co.Ltd.,PetroChina,Chengdu 610017,China;3.School of Energy Resources,China University of Geosciences,Beijing 100083,China;4.Longmatan District Carbon Black Company in Luzhou City,Sichuan Province, Luzhou 646000,China)

Liquid loading in gas well can pose a serious threat to the exploitation of natural gas.To accurately calculate the critical flow rate of gas well is vital to gas reservoir development.Currently,engineering technicians use the liquid drop model and liquid holdup model to calculate the critical flow rate for liquid loading in gas well.However,the above two old models have a significant shortcoming that the calculated result is far from the reality and can not meet the requirement of gas well development.This paper presents an artificial neural network model for predicting the minimum flow rate for continuous removal of liquids from the wellbore. The model is developed taking full advantage of the test data in gas wells,and the new model can also simplify the complex mechanism studies of liquid loading,which has a wider range of practical application.The new model has been used to calculate the actual production of gas well.The results show that the developed model can provide high accuracy in predicting liquid loading in gas well and can also determine whether there is liquid loading in gas well or not.

neural network,liquid loading in gas well,liquid drop model,liquid holdup model.

国家科技重大专项子课题“（特）低渗透油藏工程新理论与新方法”（2009ZX05009-004）资助

TE319

A

2009-12-18；改回日期：2010-07-12。

栾国华，男，1985年生，在读博士研究生，2009年毕业于西南石油大学，主要从事油气田开发方面的研究工作。E-mail：yimu851114@yahoo.com.cn。

（编辑 刘 丽）

1005-8907（2010）05-575-04

栾国华，何顺利，舒绍屹，等.应用人工神经网络方法预测气井积液［J］.断块油气田，2010，17（5）：575-578.

Luan Guohua，He Shunli，Shu Shaoyi，et al.Using artificial neural network method to predict liquid loading in gas well［J］.Fault-Block Oil&Gas Field，2010，17（5）：575-578.