经济集聚与城市经济增长——来自中国城市的经验证据

杨 扬,余壮雄,舒 元

(1.中山大学国际商学院,广东广州 519082;2.暨南大学产业经济研究院,广东广州 510634;3.中山大学岭南学院,广东广州 510275)

经济集聚与城市经济增长
——来自中国城市的经验证据

杨 扬1,余壮雄2,舒 元3

(1.中山大学国际商学院,广东广州 519082;2.暨南大学产业经济研究院,广东广州 510634;3.中山大学岭南学院,广东广州 510275)

本文利用我国 232个地级市 1999-2006年的数据,探究我国经济集聚与城市经济增长的关系,并试图考察在我国城市经济增长的过程中,Williamson假说是否成立。研究表明,在我国城市经济增长的过程中,该假说成立,即城市经济集聚与城市经济增长速度之间存在倒U型关系,在经济发展的初始阶段,经济集聚促进了城市的经济增长;而伴随经济增长,经济活动在城市的进一步集中将阻碍城市经济的增长。实证结果表明实际人均GDP水平 28283元为我国城市经济集聚与经济增长关系的临界值。

经济集聚;经济增长;Williamson假说

一、引 言

区域内的经济分工或者经济集聚是否可以促进经济增长,更进一步地说,随着时间推移,经济活动的地理位置将如何影响地区的经济增长,经济活动的地理位置与地区的经济增长之间关系如何?这是新经济地理学和城市经济学研究中的基本问题。[1-2]同时,该问题的研究对政府经济政策的制定,特别是在“促进经济整体发展,协调地区合理分工,缩小地区经济差距”的问题上具有重要的引导作用。目前,我国地区经济发展不平衡已经成为不争的事实,因此从集聚的视角研究我国经济分工与经济增长之间的关系具有重要的现实意义。而城市作为经济增长的发动机逐渐成为经济增长研究中最为重要的研究对象,因此本文将利用我国 232个地级以及地级以上城市 1999-2006年的数据,探究城市经济集聚对城市经济增长的影响[3]。

目前,已有许多模型在理论上证明了集聚对经济增长的正向促进作用,例如:Martin和Ottaviano认为经济集聚与经济增长之间存在“双向自我强化的机制”[4];Fujita和 Tisse强调,当给定了产业集聚的“外溢效应”时,“经济活动的空间集聚”将促进地区的经济增长[3]。而“经济活动的空间集聚”与“经济增长”之间并非简单的“正向促进”关系,它们之间的关系有可能受到其他经济因素的影响。

W illiamson认为,集聚对经济增长的作用与经济体所处的阶段有关,当经济体处于发展的初期阶段时,由于公共基础设施和交通基础设施的稀缺性,生产集聚将会提高资源的配置效率、使用效率,从而有效地提高生产效率,显著地促进经济增长[5]。而当经济发展到一定的阶段,由集聚所带来的“拥挤成本”将产生“负的外部性”,从而将降低生产效率;同时公共基础设施的兴建,以及通讯水平和交通基础设施的完善,将促使越来越多的生产活动转移到其他地区进行生产,因此当经济体处于较高的发展阶段时,“经济集聚”与“经济增长”之间的关系便不一定是正向促进的关系。Bertinelli和 Black通过模型论证了上述机制,模型中由集聚所产生的“正外部效应”主要体现在人才集聚所产生的人力资本对经济增长的促进[6]。

尽管国内外对经济集聚和经济增长关系的理论研究比较丰富,但由于研究数据的限制,对该问题的实证研究却相当缺乏[7-8]。Bairoch、Hohenberg和Lees从经济史的角度论证了这两者间的关系,研究结果支持两者的正向相关关系[9-10]。而问题相关的计量实证检验非常有限。Henderson以及 Marius和 Federica的研究,是运用规范计量方法探讨该问题最具说服力两篇的代表性文章[11-12]。Henderson运用 70个国家 1960-1990年的面板数据,使用差分 G MM的估计方法发现:当使用城市化水平指标衡量经济的集聚程度时,经济增长与经济集聚之间并不存在显著的相关关系;而当使用城市集中化指标(经济规模最大的几个城市占全国的经济比重)衡量经济集聚时,在经济发展水平较低的国家,经济集聚对经济增长有显著的促进作用[11]。

Marius和 Federica使用 105个国家 1960-2000年的数据,利用截面最小二乘回归和系统 G MM的估计方法得到了与 Henderson相同的结论[12,11],他们还测算出了集聚与经济增长关系的临界值约为人均GDP一万美元,即当经济体的人均 GDP小于1万美元时,集聚能够促进经济增长,而当经济体的人均GDP大于 1万美元时,集聚与经济增长为负向相关关系。

Henderson以及Marius和 Federica的实证研究都支持了前文所提到的W illiamson假说[11-12]:集聚在经济发展的初始阶段能够促进经济增长,当经济发展到某一阶段后集聚与经济增长为负向相关关系。在计量检验中,这种假说体现为经济增长对反映集聚的回归系数为正值,而经济增长对集聚与初始人均收入的交叉项回归系数为负值。

本文将利用我国 232个地级以及地级以上城市1999-2006年的数据,探究我国经济集聚与城市经济增长的关系,并试图考察在我国城市经济增长的过程中,W illiamson假说是否成立。

二、计量模型设定与估计方法

采用两种估计方法研究“经济集聚”与“经济增长”之间的关系,一种为使用“巴罗回归方程”的截面最小二乘的估计方法,另一种为采用标准MRW框架的动态面板差分 G MM和系统 G MM的估计方法。这两种方法,一种是从长期静态的角度考察“经济集聚”与“经济增长”之间的关系;另一种是从短期动态的角度对“经济集聚”与“经济增长”之间的关系进行研究。

(一)截面回归

使用“巴罗回归方程”对我国 232个地级及以上城市进行最小二乘估计,主要是为了考察经济初始状态以及某些解释变量时期内均值对 1999-2006年间的经济增长速度 (被解释变量)之间的长期关系。具体的截面回归方程如下:

其中,yip为各个城市在 1999-2006年,10年间的实际人均 GDP的增长速度,Yi0为各个城市初始的实际人均 GDP水平,代表了经济集聚的指标①关于经济集聚指标和控制变量集合的具体设定在以下数据说明中有详细的介绍。,为控制变量集,为回归残差。其中主要包括反映城市产业集聚的指标,该指标的平方项,以及城市产业集聚与城市实际人均 GDP的乘积交叉项。这里它的系数为本文的研究重点。

(二)面板回归

本文将在标准的MRW框架下,基于面板模型的分析框架考察经济增长与经济结构之间的短期动态关系。Mankiw、Romer和Weil基于新古典经济增长理论所发展的实证经济增长模型已成为实证经济增长文献的标准模型之一[13]。

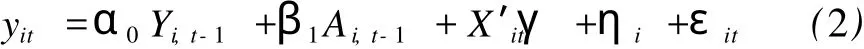
其中,yit表示地区的实际 GDP增长率,Yit表示地区实际 GDP的对数,其中,yi,t=Yi,t-Yi,t-1;Ai,t-1代表了经济集聚的指标,Xi,t为控制变量集,ηt为市别效应,εi,t是误差项,下标 i和 t各自代表城市和时间。Ai,t-1中主要包括反映城市产业集聚的指标 primacy(-1),该指标的平方项 primacy(-1)2,以及城市产业集聚与城市实际人均 GDP的对数乘积交叉项 primacy(-1)＊log〔y(-1)〕。

式(2)在宏观实证分析中已经成为一个标准模型,当样本 n很大、T有限时,普通的LSDV或ML估计会遇到偶然性参数 (Incidental Parameter)问题而无法获得参数的一致估计。为了避开偶然性参数问题,早期的研究采取的是对一阶差分后的模型进行IV估计或 G MM估计的方法。Arellano和Bond扩展了普通的 G MM估计[14],他们建议使用变量水平值的所有滞后项作为变量差分的工具变量以提高估计的有效性,这一方法也称为差分 G MM估计 (D IFG MM)。遗憾的是,后续的研究发现,差分 G MM估计在有限样本下存在较大的偏差,特别是当自相关系数比较接近 1时尤其严重。

Blundell和Bond的研究表明[15],差分 G MM估计的不良表现源于其存在的弱工具变量问题,他们建议在进行差分 G MM估计的同时使用另一组矩条件来估计参数,即使用变量的差分作为变量水平值的工具变量,这一方法也称为系统 G MM估计。Blundell和Bond的推导与模拟表明,系统 G MM估计能有效克服弱工具变量的问题,极大的改进差分G MM估计的有限样本表现,在降低偏差的同时提高了估计的精度。因此,本文的主要分析工具为系统G MM,在后面的实证中同时也给出了差分 G MM的估计结果,但研究结论以系统 G MM为准。

(三)面板回归中最优模型的选择与设定

由于代表经济集聚的指标集合中的 primacy(-1)和 primacy(-1)＊log〔y(-1)〕存在严重的共线性,不妨把两个变量合成 pr imacy(-1)＊log〔y(-1)〕-cr0,使用格点搜索方法从 log(y)的实际取值范围以一定的步长搜索,以确定 cr0的最优值,而其中cr0的最优值也即为W illiamson假说的临界值。

三、数据来源与数据说明

实证中所有的数据均来源于《中国城市统计年鉴》(1999-2006年)。其中实际 GDP分别按各个地级市的市辖区 GDP年增长率(以 1999年为基期)进行折算获得;人口是地级市的市辖区年末总人口数。人均 GDP的计算为各个城市的实际 GDP除以城市年末总人口。值得强调的是城市集聚指标 primacy的计算过程。在城市统计年鉴中,现行的城市统计设定了两个统计范畴:一个是“市辖区”,(即市辖区,包括城区和郊区);另一个是全市 (包括市辖区,下辖的县和县级市)。对于所有地级以及地级以上的城市,“全市”栏反映了整个市行政区域内的情况,而“市辖区”栏则反映了城市包括城区和郊区内的情况。利用市辖区的国内生产总值比上全市的国内生产总值,便得到了指标 pr imacy,该指标可以大致反映经济活动在城市中的集聚情况。值得强调的是,除了财政支出使用了“市辖区”的数据①由于在 2003年以前,各市的财政支出统计只包括市辖区的数据,因此在计算 gov指标时,采用了市辖区的财政支出/市辖区的国内生产总值。,其他的所有指标也均以“地区”或“全市”为统计口径。

而相关控制变量X的选取,我们使用每个城市第二产业以及第三产业占该市地区生产总值的分额s2i,t,s3i,t,代表城市内部的产业结构;使用每个城市第二产业 (第三产业)生产总值占所有城市第二产业(第三产业)生产总值的份额比例 I2i,t,T3i,t,代表城市间的产业分工。另外,使用财政支出占 GDP的比例gov代表城市中政府规模;使用市辖区的普通高等学校人数占市辖年末总人口的比例 hedu,市辖区的普通中学学生人数占市辖年末总人口的比例m edu以及市辖区的小学入学人数占市辖年末总人口的比例 pedu代表城市人力资本存量;在截面回归中,设虚拟变量policy1,其中经济特区和沿海开放城市取值为 1,其他城市为0;设虚拟变量policy2,其中副省级城市和直辖市取值为1,其他城市为0,该指标反映了改革开放初期中央的对不同城市的政策导向。另外,还专门以珠江三角城市群、长三角城市群以及环渤海经济圈的 47个城市为样本根据模型进行了估计②由于环渤海城市群中的锦州和滨州数据不全,因此排除在考察范围内。。表 1给出了本文主要研究变量初始年份和终止年份,即 1999年和2006年各个变量的描述性统计。从表 1可以看出,伴随经济的增长,与 1999年相比,2006年实际人均 G DP和城市内部经济集聚程度 pr imacy的均值以及最小值都有大幅度的增加。

表 1 主要研究变量的初始统计性描述(1999年和 2006年)

四、实证结果分析

(一)截面回归

通过表 2,发现截面回归的结果支持了W illiamson假说。因为,实际人均 GDP的增长率对 PR IMACY0的回归系数为正,而对初始集聚水平 PR IMACY0和初始实际人均 GDP的交叉项乘积系数为负值。这表明在某一临界点,城市经济集聚水平的增加将阻碍城市经济的增长。

表 2 经济增长与集聚度的截面回归(1999-2006年)

图1 格点搜索得到的[SSR,log(GDP)]组合

(二)面板回归

通过格点搜索确定了最优的实证方程形式,即当 CR0取值 10.25时,实证方程为最优。如图 1所示,图中的曲线表示 log(GDP)不同取值时所对应的残差平方和 SSR,当 SSR最小取值所对应的 log (GDP)为 CR0等于 10.25,而 CR0也即W illiamson假说的临界值。经过折合计算其对应的实际人均GDP水平约为 28283元。即以我国 232个地级市为研究对象,当人均 GDP水平小于 28283元时,经济集聚对经济增长有显著的促进作用;而当人均 GDP水平小于 28283元时,经济集聚与经济增长间呈现显著的负相关关系。

以系统 G MM的回归结果为准,结合表 3表 4我们发现经济增长速度与经济的集聚程度之间确实存在稳健的倒U型关系。在表 1中,我们将被解释变量“人均 GDP增长率”对一系列控制变量以及关注变量 primacy(-1)^2、primacy(-1)＊log〔gdp(-1)〕-cr0进行回归,回归结果表明 primacy(-1)^2与 pr imacy(-1)＊log〔gdp(-1)〕-cr0的系数显著为负。表 2则是去除表 1中不显著变量 s3、i2后的回归结果,结果表明 primacy(-1)^2与 primacy(-1)＊log〔gdp(-1)〕-cr0的系数同样显著为负,这与表 1所显示的回归结果吻合。在回归结果中,代表城市内部产业结构的控制变量 s2、代表城市产业分工的控制变量 i3以及代表城市教育水平的控制变量 hedu、medu、pedu与经济增长之间存在显著的正向关系,而代表政府行为的控制 gov与经济增长之间存在显著的负向关系。这表明在我国目前的城市经济发展阶段,经济增长速度较快的城市往往是产业结构中第二产业比重较高的城市以及产业分工中第三产业所占比重越高的城市;同时,政府干预较少、教育水平较高的城市增长速度也较高。

表 3 经济增长与集聚度的系统 G MM与差分 G MM估计 1(1999-2006年)

以上的回归结果支持了W illiamson假说,即在经济发展的初始阶段经济集聚对经济增长有显著的促进作用,而伴随经济发展,人均 GDP水平不断提高,当其超过临界值 cr0时,经济集聚与经济增长呈现显著的负相关关系。根据格点搜索的结果,实际人均 GDP水平 28283元为我国城市经济集聚与经济增长关系的临界值。可以从两方面结合解释这一经济现象,从集聚本身对经济增长的直接影响来看,已有非常多的文献从集聚的“拥挤效应”出发,论述了集聚程度的增加对经济增长的负面效应;而从集聚对经济增长的间接影响来看,除了“拥挤效应”对经济增长的直接影响,过度的经济集聚将会影响城市间资源的最优配置和产业分工的优化,从而阻碍了经济增长。根据表 1和表 2的实证结果,代表城市产业分工的控制变量 i3与经济增长之间存在显著的正向关系,即在我国目前的城市经济发展阶段,经济增长速度较快的城市往往是产业分工中第三产业所占比重越高的城市。

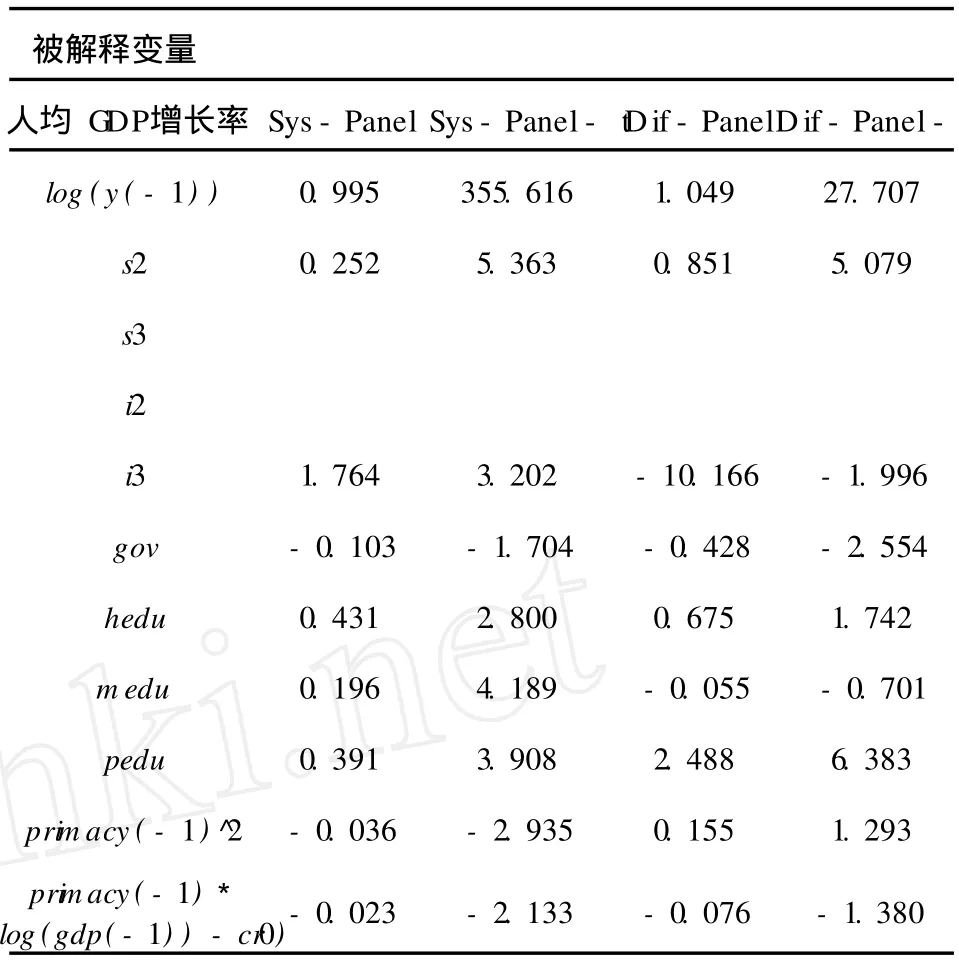
表 4 经济增长与集聚度的系统 G MM与差分 G MM估计 2(1999-2006年)

五、结 论

城市经济集聚与城市经济增长速度之间存在倒U型关系,即在城市经济发展的初始阶段,经济活动在城市内部某些区域的集聚为生产过程带来了“正外部性”,从而促进了城市的经济增长;而伴随经济增长,经济活动在城市的进一步集中将不利于城市经济的增长。这其中的原因一方面是由于集聚自身所带来的“负外部性”给经济活动带来了负面效应,另一方面从城市内经济分工的角度来看,生产活动的过度集中将不利于资源在城市内部的分配与整合,从而影响了最终的生产效率。

根据本文的实证研究,以我国 232个地级城市为研究对象,实际人均 GDP水平 28283元为我国城市经济集聚与经济增长关系的临界值。这对我国城市内部经济活动的合理分工起到了一定的指导意义,经济集聚能够促进某些发展阶段的城市增长;而伴随经济的增长,一味地鼓励经济活动在城市内部某些区域的集中将不利于经济的长期增长,而这个经济发展阶段的临界值大约相当于际人均 GDP水平 28283元的水平。该结论进一步表明,目前中央和各地政府为促进经济整体发展和缩小地区经济差距,所进行的协调地区合理分工,推进产业转移的政策是合理科学的。

[1] 梁琦.产业集聚论 [M].北京:商务印书馆,2004.

[2] (日)膝田昌久,(美)保罗·克鲁格曼.空间经济学城市、区域与国际贸易 [M].梁琦,主译.北京:中国人民大学出版社,2005.

[3] Fujita M,Tisse Jacques-Francois.Economics of agglomeration: cities, Industrial location,and regional growth[M].London:Cambridge University Press, 2002.

[4] Martin P,Ottaviano G.Growing locations:Industrial location in a model of endogenous growth[J].Journal of Public Economics,1999,73(1):85– 105.

[5] W illiamson J G.Regional Inequality and the prcessof national development:a description of the pattern[J].E-conomic Development and Cultural Change,1965,13 (1):3-45.

[6] Bertinelli L,Black D.Urbanization and growth[J]. Journal ofUrban Economics,2004,56(1):80– 96.

[7] 范剑勇.市场一体化、地区专业化与产业集聚趋势[J].中国社会科学,2004,6:39-51.

[8] 梁琦.中国工业的区位基尼系数—兼论外商直接投资对制造业集聚的影响 [J].统计研究,2003,9:21-25.

[9] Bairoch P.Economics andworld history:myths and paradoxes[M].Chicago:Chicago University Press,1993.

[10] Hohenberg P,Lees L H.The making of urban Europe [M].Chicago:Harvard University Press,1985.

[11] Henderson J V.The urbanization process and economic growth:the so-what question[J].Journal of Economic Growth,2003,8:47– 71.

[12] Brülhart M,Sbergami F.Agglomeration and growth: cross-country evidence[J].Journal of Urban Economics,2009,65:48-63.

[13] Mankiw N G,Romer D,Weil D N.A contribution to the empirics of economic growth[J].Quarterly Journal of Economics,1992,107:407-437.

[14] Arellano M,Bond S R.Some tests of specification for panel data:monte carlo evidence and an application to employment equations[J].Review of Economic Studies,1991,58:277-297.

[15] Blundell R,Bond S R. Initial conditions and moment restrictions in dynamic panel data models[J].Journal of Econometrics,1998,87:115-143.

责任编辑、校对:李斌泉

Agglomeration and Urban Econom ic Growth—Evidence from China C ities

YANG Yang1,YU Zhuang-xiong2,SHU Yuan3
(1.InternationalBusiness School,Sun Yat-sen University,Guangzhou 519082,China; 2.Institute of Industrial Economics,Jinan University,Guangzhou 510634,China; 3.LingNan College,Sun Yat-sen University,Guangzhou 510275,China)

Thispaper uses the data of China 232 prefecture-level cities through 1999-2006 to study the relationship between urban agglomeration and economic growth.Studies show that the W illiamson hypothesis is suitable for the economic growth process of China cities,with a U-inverted relationship between urban agglomeration and economic growth.Empirical results show that the level of real per capita GDP RMB 28,283 is the critical value of the relationship between urban agglomeration and economic growth.

Agglomeration;Urban economic growth;W illiamson Hypothesis

A 文章编号:1002-2848-2010(05)-0113-05

2010-05-06

本论文受中国博士后科学基金“基于专业化及多元化视角的中国城市产业分工研究”(20090460833)项目资金资助;受中山大学青年教师起步计划资金资助;受“建立宏观经济微观基础前沿问题研究:理性预期技术与转型经济”,全国优秀博士学位论文专项基金(200504)项目资助;受“‘试错法’改革的随机过程表述与有效需求管理”国家自然科学基金(70671110)资金资助;本论文受中山大学经济研究所资助。

杨扬(1982-),河南省洛阳市人,中山大学国际商学院讲师,中山大学公共管理入站博士后,研究方向:产业经济学,经济增长,公共经济学;余壮雄(1979-),广东省陆丰市人,暨南大学产业经济研究院,研究方向:计量经济学;舒元(1949-),上海市人,中山大学岭南学院院长,博士生导师,中山大学国际商学院院长,研究方向:经济增长,产业经济学,世界经济。