Mg2Si 的电子结构和热电输运性质的理论研究*

彭华王春雷 李吉超 王洪超 王美晓

(山东大学物理学院，晶体材料国家重点实验室，济南250100)

(2009年8月17日收到;2010年1月5日收到修改稿)

Mg2Si 的电子结构和热电输运性质的理论研究*

彭华†王春雷 李吉超 王洪超 王美晓

(山东大学物理学院，晶体材料国家重点实验室，济南250100)

(2009年8月17日收到;2010年1月5日收到修改稿)

利用全势线性缀加平面波法，对Mg2Si的几何结构和电子结构进行了计算，得到了稳定的晶格参数以及能带和电子态密度.能带结构表明，Mg2Si为间接带隙半导体，禁带宽度为0.20 eV.在此基础上利用玻尔兹曼输运理论和刚性带近似计算了材料的电导率、Seebeck系数和功率因子.结果表明，在温度为700K时p型和n型掺杂的Mg2Si功率因子达到最大时的最佳载流子浓度分别为7.749×1019cm－3和1.346×1020cm－3.结合实验热导参数，估算了700K时最高热电优值ZT可以达到0.93.通过对比不同温度下的输运系数发现，功率因子与弛豫时间之比的极大值随温度升高而增大，在中高温区使用材料的最佳掺杂浓度要高于低温区使用材料的最佳掺杂浓度.

Mg2Si，全势线性缀加平面波法，热电输运性质

PACC:6155H，7215，7125C，7210

1. 引言

热电材料是一类利用固体内部载流子运动实现热能和电能相互转换的功能材料.利用热电材料在进行发电和制冷过程中不需要使用传动部件，因此具有无噪声、无磨损等优点.由于近年来发展新型能源的需求，热电材料的研究已成为国际材料研究领域的热点之一［1—4］.目前应用较为广泛的热电材料主要有低温区制冷的Bi2Te3［5，6］、中温区发电的PbTe［7］以及高温区发电的SiGe［8］等传统热电材料.然而传统热电材料中含有Te，Pb等有害元素，并且原料价格昂贵，限制了其大规模的推广应用.这促使人们探寻经济且无毒环保的热电材料，其中半导体Mg2Si因具有良好的热稳定性、原材料来源广等特点，而且价格经济，已引起了人们的广泛关注.

由于本征的Mg2Si热电转换效率较低，因而人们采用掺杂、固溶等各种技术来提高Mg2Si的热电性.早期Kajikawa等［9］得到Ag掺杂的p型Mg2Si，样品在780K左右温度下功率因子S2σ(S为Seebeck系数，σ为电导率)达到0.4×10－3W/m·K2.最近Tani和Kido［10］采用等离子体火花烧结技术得到未掺杂的Mg2Si在700K时热电优值ZT为0.04左右，S2σ为0.25×10－3W/mK2.而掺杂量为0.5%的掺Sb的n型Mg2Si，S2σ最大值提高到3.4×10－3W/mK2，掺杂量为2%的样品在862 K时ZT值达到0.56，热电性能得到了极大提高.Zhang等［11，12］通过掺入Sb，La等元素来提高Mg2(SiSn)固溶体的热电性质，使这类材料的热电性能得到了进一步的提高，其中Sb掺杂的Mg2(SiSn)固溶体最大ZT值在783 K时约为0.7，La掺杂的样品750K下ZT值达到0.75.这些实验工作充分表明Mg2Si是一种非常有潜力的热电材料.

相对于材料的实验研究工作，有关Mg2Si热电性质的理论研究开展较少.早期Corkill和Cohen［13］采用第一性原理赝势方法计算6种ⅡA-Ⅳ化合物的结构、成键和电子结构，其中得到Mg2Si的禁带宽度为0.118 eV.Tani和Kido［14］采用第一性原理方法(CASTEP软件)结合线性响应方法研究了Mg2Si和Mg2Ge的晶格动力学特性，得到比热容和德拜温度随温度的变化关系.用同样的方法他们又计算了As，P，Sb等元素掺入Mg2Si的形成能和Mulliken电荷，发现这些掺杂元素都有很好的固溶性［15］.刘娜娜等［16］采用第一性原理方法(CASTEP软件)结合线性响应方法研究了Mg2Sn的电子结构和热力学性质，得到与实验值基本符合的热导率.Akasaka等［17］利用全势线性缀加平面波(FLAPW)方法(ABCAP软件)计算了n型掺杂和p型掺杂的Mg2Si的电子结构，并结合玻尔兹曼方程计算了它们的传输性质.文献［17］报道，本征和Bi掺杂的Mg2Si的Seebeck系数与实验结果较为符合，而Ag掺杂的p型样品的理论结果与实验符合不够理想.然而对于Mg2Si输运性质与掺杂浓度的关系以及体系的最佳掺杂量方面作者尚未见有系统研究的报道.本文利用FLAPW方法计算Mg2Si的几何和电子结构，然后结合玻尔兹曼输运方程计算Mg2Si的输运系数，并讨论了Mg2Si的输运系数随掺杂量的变化关系以及温度对输运性能的影响.

2. 模型与计算方法

Mg2Si具有反萤石型结构，空间群为Fm3m，晶体结构如图1所示.Si原子位于晶胞的面心和8个顶角的位置，Mg原子处在8个小立方体的中心，位于(0.25a0，0.25a0，0.25a0)处，其中a0为晶格常数.计算中采用一个Mg2Si晶胞模型，包含8个Mg原子和4个Si原子.对于电子结构的计算，我们利用了基于FLAPW计算方法的Wien2K软件包［18］，采用广义梯度近似(GGA)下的Perdew-Burke-Ernzerhof(PBE)交换关联势［19］，自洽求解Kohn-Sham方程.收敛参数RMTKmax的值设为8.0，其中RMT是糕模半径，Kmax是平面波展开式中最大的倒格子矢量.计算时Mg和Si原子的RMT取值都为0.13nm，自洽计算的能量收敛标准为1×10－5Ry.在结构优化和自洽计算中采用布里渊区10×10×10的k网格点.

热电输运系数是通过半经典的玻尔兹曼电输运方程和刚性带近似(RBA)计算得到［20—26］，其中使用了平滑的傅里叶变换以得到能带的解析形式.在计算输运性质中，对碰撞项作弛豫时间近似［20，27］.设某时刻载流子分布函数为f，而平衡状态的分布函数为f0，分布函数遵从费米-狄拉克分布.碰撞后的分布函数产生变化，有

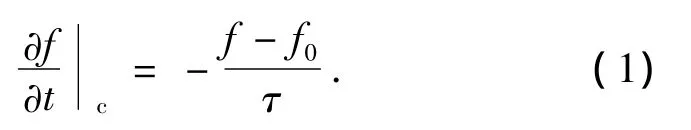
这里τ为弛豫时间，在计算中假定τ依然是温度和掺杂量的函数，但在温度和化学势一定时，弛豫时间τ和波矢k都与能量无关，这种近似计算所得结果与实验结果符合很好［21，24］.

图1 Mg2Si的晶体结构

RBA方法应用于输运计算是基于输运分布函数的基础上，输运分布函数为

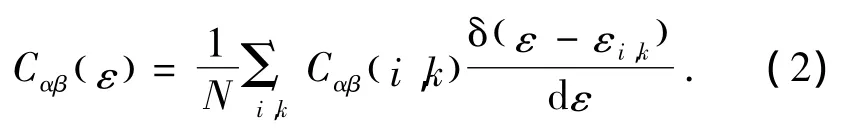
这里

其中α和β为张量指数，N为k点个数，ε(i，k)为能带的能量，i为能带指数，μ为化学势，v(k)为k空间中载流子的群速度，它是电子色散关系(能带)的梯度［28］.通过对输运分布张量积分得到输运系数，它是温度和化学势的函数，即

这里e和Ω分别为电子的电荷量和原胞的体积，T为绝对温度，σαβ为电导率张量.Seebeck系数张量表示为

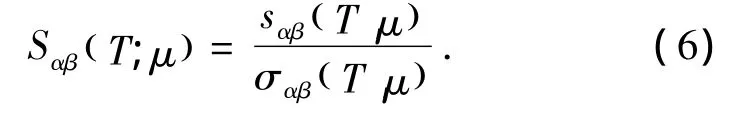
由于布里渊区的k网格点对输运性质的计算影响较大，为提高计算的精度，我们增加了k点的个数，计算了布里渊区中24000个k点的本征值.

3. 电子结构

经过GGA优化得到体系稳态时Mg2Si的晶胞体积约为0.2588nm3，因此得到Mg2Si的晶格常数为0.6373nm，计算结果与实验值［29］(0.6338nm)基本相同，说明我们选择的计算参量比较合适.在此基础上，采用GGA方法对稳定的晶格结构进行电子结构计算.

计算得到Mg2Si沿布里渊区高对称性方向的能带结构如图2所示，图中水平虚线为费米能级的位置，将费米能级选为能量零点，其他能量是以费米能级为参照标准的相对值.从能带图中可以看出，价带顶和导带底分别位于Γ(0，0，0)和X(0.5，0，0.5)点，说明Mg2Si为间接带隙半导体.得到的带隙为0.20 eV，与其他采用PBE交换势的计算结果相近［30］，但比实验上通过测量霍尔系数和电阻率得到的带隙值［31］0.78 eV要小，这是由于密度泛函理论会普遍低估带隙值所造成的.图3是Mg2Si的分波态密度，可以看出能量在9—－8 eV和－5—10 eV范围内，Mg原子和Si原子轨道都有一定的杂化.其中能量较小的范围(－9—－8 eV)的能态密度主要由Si原子的3s态电子提供，Si的3p态电子对－5—10 eV范围的态密度贡献较大.由于材料的电输运性质和载流子的类型主要由费米能级附近的电子结构决定，因此我们只关注费米能级附近的能态密度.从图3可以明显看出，Mg2Si价带顶附近的能态密度主要由Si的3p态电子和Mg的3p态电子贡献，靠近导带底的能态密度主要由Mg原子提供.

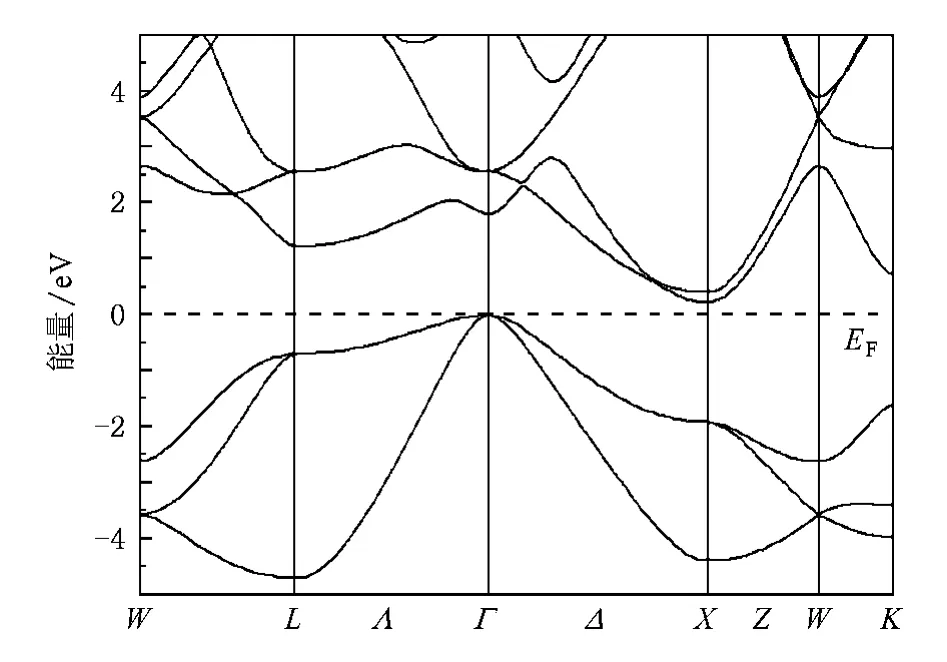
图2 Mg2Si的能带结构

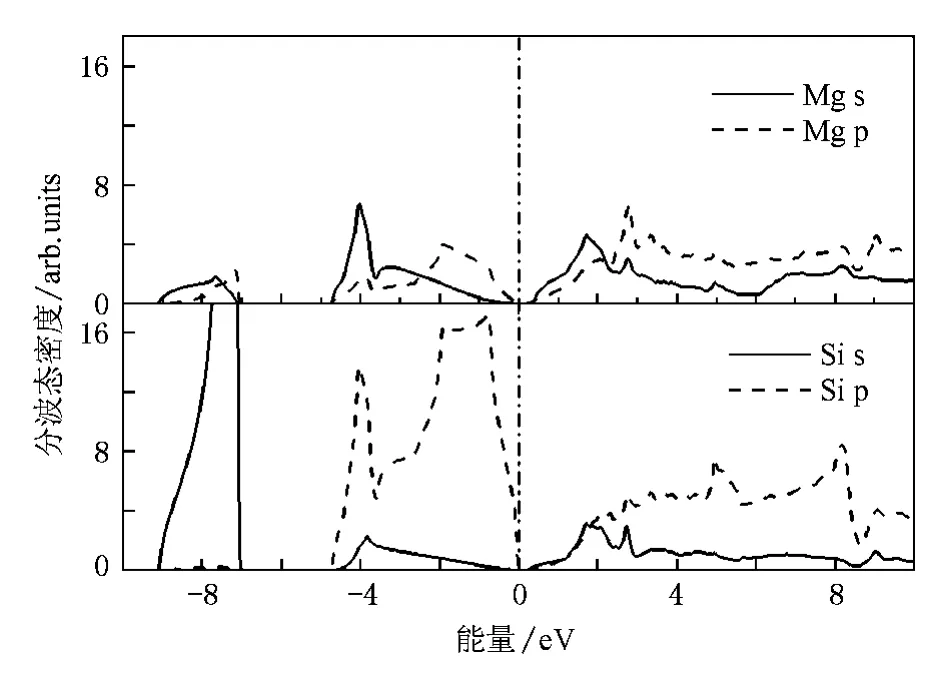
图3 Mg2Si的分波态密度

4. 输运性质

在FLAPW方法计算得到布里渊区k点本征值的基础上，采用玻尔兹曼输运方程计算了Mg2Si的热电输运系数.由于Mg2Si为适合中温区使用的热电材料，因此我们研究温度为700K时的输运系数随掺杂浓度的变化趋势.计算中我们忽略温度对能带的影响，通过费米能级的上下移动来模拟n型掺杂和p型掺杂，即采用RBA方法［18，24］.当n型掺杂时，费米能级向上移动，而p型掺杂时费米能级向下移动.图4给出了700K时掺入受主元素和施主元素后电导率与弛豫时间之比σ/τ随掺杂浓度n的变化.这里掺杂浓度n定义为单位原胞内掺入的电子或空穴数.从图4可以看出:随掺杂浓度n的增加σ/τ呈上升趋势，但p型掺杂的σ/τ值比n型掺杂的值要小.这主要是由于价带顶和导带底的能带曲率不同，即k空间中载流子的群速度不同.由于价带顶附近的色散曲线的曲率小于导带顶的曲率，从而导致(2)式中的n型掺杂的输运分布函数Cαβ值大于p型掺杂的Cαβ值，进而有n型掺杂的σ/τ值大于p型掺杂的σ/τ值.

为研究掺杂浓度对Seebeck系数的影响，我们分别给出了p型掺杂和n型掺杂的Seebeck系数随掺杂浓度的变化，如图5所示.从图5可以看出，随掺杂浓度的增大，所得到的p型掺杂和n型掺杂的Seebeck系数绝对值都是先增大后减小.这一趋势与Bi2Te3和CoSb3的理论计算结果［18］以及笼状Si结构的计算结果［23］趋势相同.由于本征的Mg2Si具有较低的载流子浓度，此时Seebeck系数值较大.当掺入受主或施主元素时，载流子浓度增加，费米能级移向价带或导带，导致Seebeck系数减小［22］.当费米能级探入价带或导带内，Seebeck系数趋于零.从图5可以看出，Seebeck系数最大值分别为232.73和249.63 μV·K－1，此时对应p型掺杂和n型掺杂浓度n分别是0.0046和0.00396，即平均一个原胞掺入受主元素提供0.0046个空穴，或者掺入施主元素引入0.00396个电子.换言之，p型掺杂和n型掺杂的掺杂量为0.46%和0.39%时是Seebeck系数最大时的掺杂浓度.

图4 σ/τ随掺杂浓度n的变化(a)p型掺杂，(b)n型掺杂

图5 Seebeck系数S随掺杂浓度n的变化(a)p型掺杂，(b)n型掺杂

温度为700K时的p型掺杂和n型掺杂的功率因子S2σ与弛豫时间τ之比S2σ/τ随掺杂浓度的变化关系如图6所示.从图6可以看出，p型掺杂和n型掺杂的功率因子随掺杂浓度的增加先增大后减小，最大Seebeck系数并不对应最大功率因子，S2σ/τ最大值的位置相对于Seebeck系数的峰值位置向两侧偏移，即获得功率因子最大值的最佳掺杂浓度比获得Seebeck系数最大值对应的掺杂浓度要大.在温度为700K时Mg2Si的p型掺杂和n型掺杂的最佳掺杂浓度n分别为0.0338和0.0588，对应材料内部的载流子浓度分别是7.749×1019cm－3和1.346×1020cm－3.此时，费米能级的位置相对于未掺杂时的费米能级分别向下移动了0.2168 eV和向上移动了0.4104 eV.对比图6(a)和(b)可以看出，n型掺杂的S2σ/τ值比p型掺杂的对应值大.由于n型掺杂和p型掺杂时载流子类型不同对弛豫时间τ造成的影响也不同，因此要对比不同掺杂类型的热电性能需要进一步计算弛豫时间的值.

为估计掺杂Mg2Si的ZT值，我们采用文献［32］实验测得未掺杂的Mg2Si晶体700K时的晶格热导率κl=4 W/mK.电子热导率通过Wiedemann-Franz定律κe=LσT计算得到，其中L为洛伦兹常数，L=2.45×10－8V2/K2.此外，采用文献［30］实验中掺杂Sb的Mg2Si载流子浓度为8.9×1019cm－3时的电导率σ=8.72×10－4Ωcm，同时采用计算得到的相同载流子浓度下的σ/τ=8.46×1019Ω－1ms－1，得出弛豫时间τ=2.1×10－14s.进而得到电导率随掺杂浓度的变化关系.假定弛豫时间不随掺杂量的变化而变化，由ZT=σS2T/(κl+LTσ)计算得到700K时最大ZT值可以达到0.93.因此，Mg2Si在优化载流子浓度后可以获得较高的ZT值.

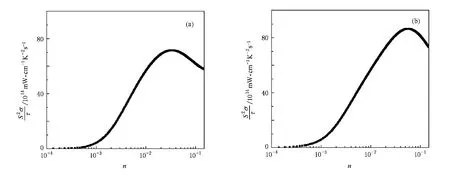
图6 S2σ/τ随掺杂浓度n的变化(a)p型掺杂，(b)n型掺杂

为研究输运系数和最佳掺杂量随温度的变化关系，我们估算了不同温度下的最佳掺杂浓度、最佳载流子浓度以及所对应的Seebeck系数和功率因子与弛豫时间的比值.表1给出了温度为300，500，700和900K时所对应的最佳掺杂浓度、最佳载流子浓度和相对应的Seebeck系数和功率因子的值.可以看出，在高温时，Mg2Si达到最大功率因子所需要的最佳掺杂浓度增加，p型掺杂的最佳载流子浓度在300K时为0.0087，而在900K时为0.0581.n型掺杂的最佳掺杂浓度在300K时为0.0383，而在900K时为0.0717.在最佳掺杂浓度时，n型掺杂和p型掺杂的Mg2Si的最大功率因子与弛豫时间的比值在高温时相对低温时要高.由表1给出不同掺杂类型的数值对比可以看出，p掺杂时的Seebeck系数比n掺杂的Seebeck系数大.对比不同掺杂类型的S2σ/τ的值可以看出，温度为300K时p型掺杂的最佳掺杂浓度对应的S2σ/τ值要比n型掺杂的S2σ/τ值大，而在温度为500，700，900K时n型掺杂的S2σ/τ值要比p型掺杂的S2σ/τ值大.

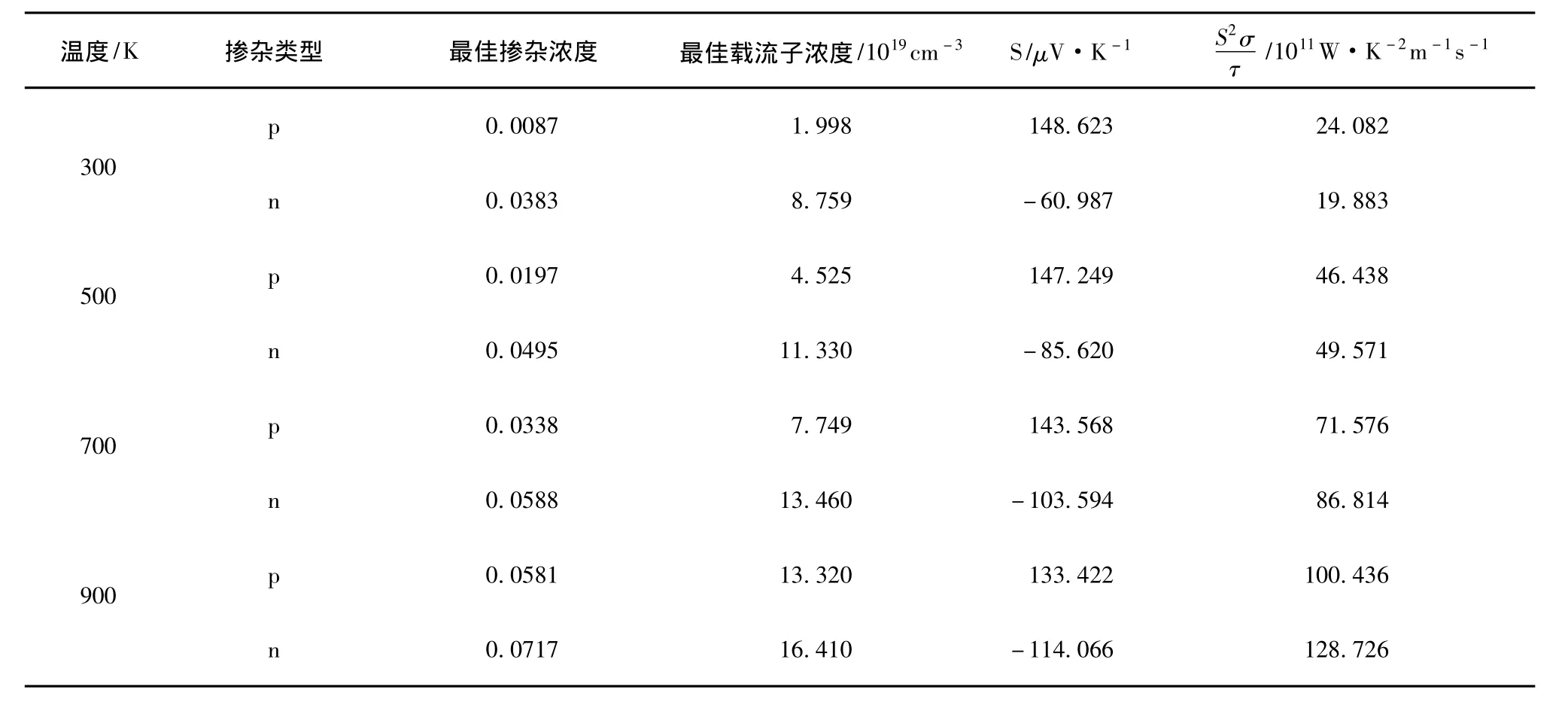
表1 估算Mg2Si的ZT值时所用参数

5. 结论

由第一性原理方法对Mg2Si的电子结构研究显示Mg2Si是间接带隙半导体，价带顶附近的能态密度主要由Si的3p态电子和Mg的3p态电子贡献，靠近导带底的能态密度主要来源于Mg原子.由玻尔兹曼输运理论和RBA所得到的传输性质表明，适度掺杂可以有效地提高Mg2Si的热电性能.本文给出了p型掺杂和n型掺杂的Mg2Si最佳掺杂浓度的值，以及最佳掺杂浓度时Seebeck系数随温度的变化.研究发现，在低温区(300K左右)p型掺杂的功率因子与弛豫时间的比值大于n型掺杂的相应值，而中高温区(700K左右)的情况却相反，n型掺杂的功率因子与弛豫时间的比值大于p型掺杂的相应值.结合实验的热导率参数，估算了典型温度(700K)时最大ZT值可以达到0.93.

［1］Liu W S，Zhang B P，Li J F，Zhang H L，Zhao L D 2008 Acta Phys.Sin.57 3791(in Chinese)［刘玮书、张波萍、李敬锋、张海龙、赵立东2008物理学报57 3791］

［2］Hochbaum A I，Chen P K，Delgado R D，Liang W J，Garnett E C，Najarian M，Majumdar A，Yang P D 2008 Nature 451 163

［3］Tang X F，Chen L D，Goto T，Hiraial T，Yuan R Z 2002 Acta Phys.Sin.51 2823(in Chinese)［唐新峰、陈立东、後藤孝、平井敏雄、袁润章2002物理学报51 2823］

［4］Cai K F，Yan C，He Z M，Cui J L，Stiewe C，Müller E，Li H 2009 J.Alloys Compd.469 499

［5］Goldsmid H J 1964 Thermoelectric Refrigeration(New York: Plenum)p37

［6］Jang J，Xu G J，Cui P，Chen L D 2006 Acta Phys.Sin.55 4849(in Chinese)［蒋俊、许高杰、崔平、陈立东2006物理学报55 4849］

［7］Tung Y W，Cohen M L 1969 Phys.Rev.180 823

［8］Heller M W，Nasby R D，Johnson R T 1976 J.Appl.Phys.47 4113

［9］Kajikawa T，Shida K，Shiraishi K，Ito K，Omori T，Hirai M，Shonan T 1998 Proceedings of the 17th International Conference on Thermoelectrics(Nagoya:IEEE)p362

［10］Tani J I，Kido H 2007 Intermetallics 15 1202

［11］Zhang Q，Yin H，Zhao X B，He J，Ji X H，Zhu T J，Tritt T M 2008 Phys.Stat.Sol.(a)205 1657

［12］Zhang Q，He J，Zhao X B，Zhang S N，Zhu T J，Yin H，Tritt T M 2008 J.Phys.D 41 185103

［13］Corkill J L，Cohen M L 1993 Phys.Rev.B 48 17138

［14］Tani J I，Kido H 2008 Comput.Mater.Sci.42 531

［15］Tani J I，Kido H 2008 Intermetallics 16 418

［16］Liu N N，Song R B，Sun H Y，Du D W 2008 Acta Phys.Sin. 57 7145(in Chinese)［刘娜娜、宋仁伯、孙翰英、杜大伟2008物理学报57 7145］

［17］Akasaka M，Iida T，Matsumoto A，Yamanaka K，Takanashi Y，Imai T，Hamada N 2008 J.Appl.Phys.104 013703

［18］Blaha P，Schwarz K，Madsen G K H，Kvasnicka D，Luitz J 2001 WIEN2K，An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties(Vienna:Technische Universitt Wien)

［19］Perdew J P，Burke K，Ernzerhof M 1996 Phys.Rev.Lett.77 3865

［20］Madsen G K H，Singh D J 2006 Comput.Phys.Commun.175 67

［21］Lykke L，Iversen B B，Madsen G K H 2006 Phys.Rev.B 73 195121

［22］Yang J，Li H M，Wu T，Zhang W Q，Chen L D，Yang J H 2008 Adv.Funct.Mater.18 2880

［23］Singh D J 2008 Phys.Rev.B 76 085110

［24］Wang W，Wang Z Y，Wang L L，Liu H J，Shi J，Li H，Tang X F 2009 J.Appl.Phys.105 013709

［25］Li J C，Wang C L，Wang M X，Peng H，Zhang R Z，Zhao M L，Liu J，Zhang J L，Mei L M 2009 J.Appl.Phys.105 043503

［26］Akasaka M，Iida T，Matsumoto A，Yamanaka K，Takanashi Y，Imai T，Noriaki H 2008 J.Appl.Phys.104 013703

［27］Feng D，Jin G J 2003 Condensed Matter Physics(Vol.1) (Beijing:Higher Education Press)p227(in Chinese)［冯端、金国钧2003凝聚态物理学(上卷)(北京:高等教育出版社)第227页］

［28］Scheidemantel T J，Ambrosch-Draxl C，Thonhauser T，Badding J V，Sofo J O 2003 Phys.Rev.B 68 125210

［29］Anastassakis E，Hawranek J P 1972 Phys.Rev.B 5 4003

［30］Kalarasse F，Bennecer B 2008 J.Phys.Chem.Solids 9 1775

［31］Morris R G，Redin R D，Danielson G C 1958 Phys.Rev.109 1909

［32］Akasaka M，Iida T，Nemoto T，Soga J，Sato J，Makino K，Fukano M，Takanashi Y 2007 J.Cryst.Growth 304 196

PACC:6155H，7215，7125C，7210

*Project supported by the State Key Development Program for Basic Research of China(Grant No.2007CB607504).

†E-mail:penghua@mail.sdu.edu.cn

Theoretical investigation of the electronic structure and thermoelectric transport property of Mg2Si*

Peng Hua†Wang Chun-Lei Li Ji-Chao Wang Hong-Chao Wang Mei-Xiao
(State Key Laboratory of Crystal Materials，School of Physics，Shandong University，Jinan250100，China)
(Received 17 August 2009;revised manuscript received 5 January 2010)

Full-potential linearized augmented plane wave method and Boltzmann transport properties have been used to investigate the crystal structure and electronic structure of Mg2Si.Electronic conductivity，Seebeck coefficient and power factor are calculated.Energy band structure shows that Mg2Si is an indirect semiconductor with energy band gap of about 0.20 eV.Transport properties versus the doping level have been calculated for the n type and p type doped materials at 700K.The optimal carrier concentration corresponding to the maxima of power factor are obtained，which are 7.749× 1019cm－3and 1.346×1020cm－3for the p-doping and n-doping respectively.Maximum ZT value of 0.93 has been estimated in combination with experimental data of thermal conductivity.From the transport properties at different temperatures，we found that the ratio of power factor to relaxation time is enhanced when the temperature increases. Optimum doping level of materials used in middle and high temperature range is higher than that of materials used in low temperature.

Mg2Si，full-potential linearized augmented plane wave method，thermoelectric transport property

book=261,ebook=261

*国家重点基础研究发展计划(批准号:2007CB607504)资助的课题.

†E-mail:penghua@mail.sdu.edu.cn