利用Gupta势结合遗传算法研究ConCu55－n(n=0—55)混合团簇的结构演化及基态能量*

鄂箫亮 段海明

(新疆大学物理科学与技术学院，乌鲁木齐830046)

(2009年9月13日收到;2009年12月3日收到修改稿)

利用Gupta势结合遗传算法研究ConCu55－n(n=0—55)混合团簇的结构演化及基态能量*

鄂箫亮 段海明†

(新疆大学物理科学与技术学院，乌鲁木齐830046)

(2009年9月13日收到;2009年12月3日收到修改稿)

采用半经验的Gupta多体势结合遗传算法对ConCu55－n(n=0—55)混合团簇的基态结构和能量进行了研究，发现这些混合团簇的基态结构是在Co55，Cu55单质团簇(Mackay二十面体)的基础之上发生的畸变;从n=0(Cu55)开始，Co原子从中心到表面，从棱到顶点依次、连续替换Cu原子;基态结构与键能较大键的数目及其平均键长有关; Co13Cu42具有最稳定的结构，13个Co原子全部位于团簇内部形成Mackay二十面体对整个团簇的稳定性有显著影响.

团簇，结构和能量，Gupta势，遗传算法

PACC:7115Q，3640B

1. 引言

团簇的几何结构决定着团簇的物理、化学性质，直接影响着纳米材料的应用与发展.在实验上很难测定含原子数较少的自由团簇的基态结构，因而通过理论计算获取其基态结构信息成为一种必不可少的手段.目前的理论计算方法主要有基于量子力学层次上的第一性原理、从头计算方法和应用势模型来处理多体问题的经验、半经验方法.前者的计算结果非常精确，但计算量极大，很难处理原子数较大的体系;后者可按其模拟方式的不同分为模拟退火［1］、分子动力学［2］、蒙特卡洛［3］和遗传算法等［4，5］.

Co，Cu团簇作为重要的催化剂早已引起了广泛的关注，科研工作者已对其相关性质进行了大量的研究［6—16］.随着计算条件的不断改善和应用的需求，对混合团簇的结构与物性的研究日益受到重视:Sondón等人为了研究Ni-Rh混合团簇的磁性，利用Gupta势结合分子动力学模拟计算了其基态结构［17］;Feng等人利用密度泛函理论计算了Cu-Ni小团簇的结构、稳定性和磁矩［18］;Wang等人也利用密度泛函理论计算了Cu-Au小团簇的结构和电子性质［19］.然而对于Co-Cu混合团簇的研究却很少，Co55，Cu55都具有稳定的二十面体结构，但对其混合团簇的研究仍是一个空白.

本文的主要目的是通过计算ConCu55－n(n=0—55)混合团簇的基态结构和能量得到总原子数为55时Co-Cu混合团簇的结构演化规律及其稳定性.采用改进的遗传算法和用于模拟过渡金属及其合金的半经验Gupta多体势［20］，所得结果可以为以后的实验以及更大数目混合团簇的研究提供一定的参考.

2. 计算方法

2.1. 遗传算法

遗传算法是一种模拟生物进化的全局最优化方法，主要由交配算子和变异算子构成.交配算子是根据群体中初始个体的能量计算相应的适配度，然后根据适配度选择交配所需的父母团簇，能量越低选择概率越大，最后用一个过质心的平面把父、母团簇分成两半，将父团簇的一半与母团簇的另一半组合成一个子团簇，要求该子团簇的总原子数与父母团簇相等;变异也是根据群体中团簇的适配度随机选取某个团簇，再随机选取该团簇的若干原子在任意方向移动固定的距离而得到子团簇;将得到的子团簇进行弛豫，再与群体中的团簇进行比较:若其能量与群体中的团簇都不相等且其能量比群体中能量最高者低则替换群体中能量最高者，反之则抛弃.每执行一次称为一代，遗传算法就是通过一代代的循环最终找到能量最低的结构.

混合团簇的情况比单质团簇复杂得多.交配时不但要保证团簇的总原子数不变，而且要保证团簇中每种原子的个数不变.即使它们的几何结构极其相近，但由于两种原子位置的不同，可能出现许多不同能量的团簇，通常两种原子数越接近这样的团簇越多.这大大增加了寻找基态结构的难度，若按照以上的算法常常会找不到基态结构.Darby等人计算的Cu21Au21混合团簇的基态能量为－136.554451 eV［21］，我们通过计算发现其基态能量应为－136.557809 eV.比较了两者的几何结构，发现几乎完全相同，其能量的差异在于团簇中Cu，Au原子的位置不同.因此，我们引入了交换算子，即根据适配度随机选取某个团簇，再随机选取该团簇中一个第一种原子和一个第二种原子，互换它们的位置，然后再选取再互换(不能选取以前选过的两个原子)，经过若干次互换后得到子团簇.在程序中，我们将交配、变异、交换三种算子并列，通过计算发现，选择这三种算子的概率分别为0.5，0.1，0.4时效率较高.

在计算中还发现，对于给定原子个数的团簇，能量较低的结构往往会集中于某些特定的几何构型上，为了提高计算效率，尽可能保持群体中团簇几何构型的多样性，在运行交换算子时，对子团簇进行弛豫后，不是替换群体中能量最高的团簇而是与所选团簇的能量进行比较，当子团簇的能量不等于群体中其他团簇的能量且比所选团簇低时，替换该团簇，否则抛弃.

2.2. Gupta多体势

用来描述过渡金属及其合金的Gupta多体相互作用势，其形式由成对的Born-Mayer排斥项和含多体效应的吸引项组成.后者取自紧束缚模型电子态密度的二次矩近似.这种势模型被广泛地用来模拟各种过渡金属体系，其形式是

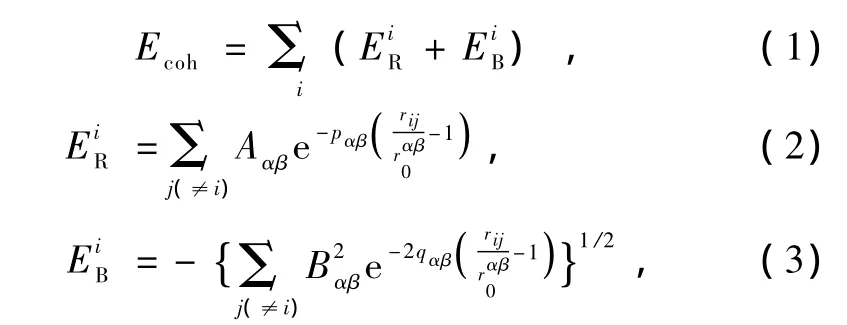
其中Ecoh，EiR，EiB分别代表体系的结合能、第i个原子受到其他原子的排斥能和吸引能，其中rij为原子间距，r0αβ是两类原子(α和β)间的特征长度，对于块体材料就以第一近邻距离表示，Aαβ是衡量原子间排斥强度的量，Bαβ是有效跳跃积分通常只与原子类别有关.

表1中列出了Co-Cu体系的参数A，p，q，B和r0的值［22］.这些参数是通过拟合块体材料的束缚能、晶格常数、体弹模量及弹性扭转常数而得到的.

表1 Co-Cu混合团簇的Gupta势参数

Cu晶体是fcc结构，Co晶体是hcp结构，Gupta势对其分别考虑到第五、九近邻原子［20］，对Co-Cu相互作用也考虑到第九近邻原子［22］.

3. 结果与讨论

3.1. 几何结构

Co55，Cu55团簇的基态处于稳定的Mackay二十面体结构，具有Ih对称性［10，11，21］，我们计算的结果也与其完全符合，ConCu55－n(n=0—55)混合团簇基态结构的形状与Co55，Cu55非常相似.为了精确的描述这些混合团簇与Co55，Cu55单质团簇之间的差异，可以引入相似函数S，

式中，R0为该团簇的几何中心为混合团簇中第n个原子到其几何中心的距离;r′n为所比单质团簇中相应原子到其几何中心的距离.混合团簇与所比单质团簇越相似，S值越趋近于1，反之则趋近于0.先前的一些文章也曾用它对混合团簇与其相应的单质团簇进行比较［23，24］.

图1是ConCu55－n(n=0—55)混合团簇基态结构随Co原子数增加与Co55，Cu55相比较的相似函数曲线图(S曲线)，从中可以看出S的值在0.9—1之间，说明这些混合团簇的基态结构是在Co55，Cu55单质团簇二十面体基础之上的畸变.通过比较发现，当n=13(Co13Cu42)时曲线出现了转折点，说明在这一点前后混合团簇基态结构的形状变化较大.这是由于Co原子位于团簇内部和表面时对团簇尺寸的影响不同而造成的，当Co原子位于团簇内部(n= 1—13)时对团簇尺寸的影响较大，S曲线比较陡;当Co原子位于团簇表面大多数位置时对团簇尺寸的影响较小，S曲线比较平滑;但随着n的不断增大，Co原子逐步占据表面所有位置，混合团簇尺寸迅速向Co55靠近，S曲线再次变陡.在这些混合团簇中，Co，Cu原子是混合还是分离的呢?为此，我们计算了这些混合团簇基态结构中两种原子质心之间的距离，用以判断每种组分下基态结构中两种原子的分布状况(混合、分离).通常来说质心间距越大两种原子越趋于分离状态，反之趋于混合状态;但在质心间距趋于零时可能出现两种情况:一是两种原子完全混合;二是出现二十面体典型的壳层结构［25］(一种原子占据内层，另一种原子占据外层，虽然质心重合但整个团簇处于完全分离状态).图2绘出了这些混合团簇基态结构中两种原子的质心间距随Co原子个数增加的变化曲线，从中可以看出随着Co原子数的增多质心间距呈波浪式变化.当Co原子数为1，13，43时，混合团簇中两种原子的质心间距等于零，Co原子数为27，28时质心间距非常小(约0.04).作为补充，我们又计算了这些团簇的原子径向分布，用棱(E)和顶点(V)来描述Mackay二十面体:在Cu55中，有一个中心、第一层有12个顶点(1V(12))、第二层有30个棱(2E(30))和12个顶点(2V(12)).图3绘出了Cu55，Co13Cu42，Co27Cu28，Co28Cu27，Co43Cu12，Co54Cu1团簇基态结构中两种原子的径向分布(按0.02统计，即两原子到质心距离相差小于0.02时，就认为这两个原子到质心的距离相同).虽然棱位置与顶点位置距中心的距离相差不大，但对混合团簇来说这两种位置上原子种类的不同对团簇的结构和能量有着很大的影响.

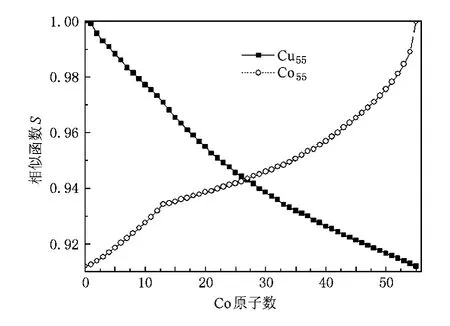
图1 ConCu55－n(n=0—55)混合团簇基态结构随Co原子数增加相似函数S的变化曲线

图2 ConCu55－n(n=0—55)混合团簇基态结构随Co原子数增加两种原子质心间距的变化曲线

在图1中，n=1—13时，S曲线较陡是因为Co原子占据中心和1 V位置;n=14—43时，S曲线较平缓是由于Co原子占据2E位置;当Co原子占据2 V位置(n>43)时，S曲线再次变陡.由于2E与2V位置距中心的距离相差不大，故没有出现明显的转折点.由此看出，Co原子占据中心，1V，2E，2V位置直接影响着团簇的尺寸.

图4是部分混合团簇的基态结构图，由图2、图3和图4可知Co13Cu42中13个Co原子占据团簇内部，形成Co13Mackay二十面体结构，42个Cu原子将其紧密包围起来，整个团簇呈分离状态;对于Co27Cu28Co28Cu27团簇，在13个Co原子占据团簇内部后，剩下的Co原子占据位于表层的棱位置.由于顶点和棱位置的交替出现，使得整个团簇处于混合状态;Co43Cu12中43个Co原子完全占据团簇内部和表层棱位置，12个Cu原子全部位于表层顶点位置，该团簇完全处于混合状态.

图3 Cu55，Co13Cu42，Co27Cu28，Co28Cu27，Co43Cu12，Co54Cu1团簇基态结构中Co，Cu原子的径向分布图

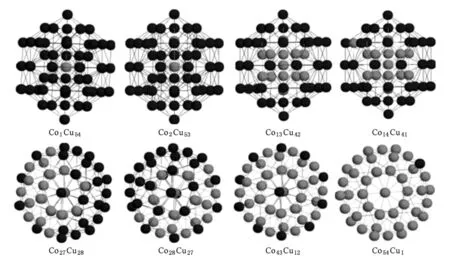
图4 Co1Cu54，Co2Cu53，Co13Cu42，Co14Cu41，Co27Cu28，Co28Cu27，Co43Cu12，Co54Cu1团簇的基态结构图，其中黑色代表Cu原子，灰色代表Co原子

通过上面的分析可以看出在ConCu55－n(n=0—55)混合团簇的基态结构中Co原子从内向外依次替换Cu原子，其中两种原子混合较少，分离较多.为了确保Co原子依次替换Cu原子的严密性，再次计算了每个混合团簇中每种原子的表体比.表体比函数S定义为

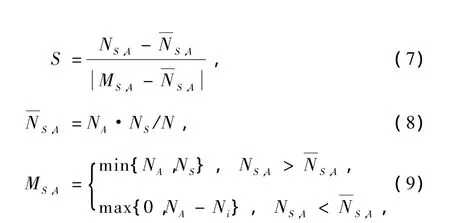
N是混合团簇中原子的总个数，NA为该团簇中A类原子总数，NS是该团簇中位于表面的原子总个数，NS，A表示位于混合团簇表面的A种原子的个数，该团簇内部的原子总个数Ni=N－NS.S的值在－1—1之间变化，S>0表示A种原子在团簇表面要比在内部多，S<0则相反.Zhang等也用这种方法分析过Cu-Au，Cu-Ag，Au-Ag混合团簇的相关性质［26］.

我们的计算结果显示在ConCu55－n(n=0—55)混合团簇基态结构中对于Co原子S值全部等于－1，Cu原子全部等于1，说明在ConCu55－n(n=0—55)混合团簇基态结构演变过程中Co原子将团簇内部的Cu原子全部替换后再替换表面的Cu原子，也就是说在演变过程中Co原子严格从内向外替换Cu原子.

那么对于那些等价的位置，在ConCu55－n(n= 0—55)混合团簇结构演化过程中Co原子是怎样替换Cu原子的呢?为了研究这一过程我们对这些团簇中基态和部分激发态结构的各种键数(Co—Co，Cu—Cu，Co—Cu)、键长(指平均键长)以及对称性进行了计算和分析.

以表1中的r0为参考，若rij≤1.2r0则认为这两个原子成键［27］(事实上，在二十面体结构中当取值为1.1r0到1.3r0时，所得结果完全相同).为比较键能的大小，计算了Co2，Cu2，Co1Cu1团簇的基态能量，分别为－3.150612 eV，－2.581510 eV，－2.801267 eV;这种方法虽然不能精确地描述这三种键能的大小，但可以粗略地比较它们的差异:Co-Co键能最大，Co-Cu次之，Cu-Cu最小.表2列出了在几种典型的组分下，混合团簇的各种键数、平均键长以及对称性.其中［1］表示基态，［2］，［3］，［4］是离基态能量较近的激发态.

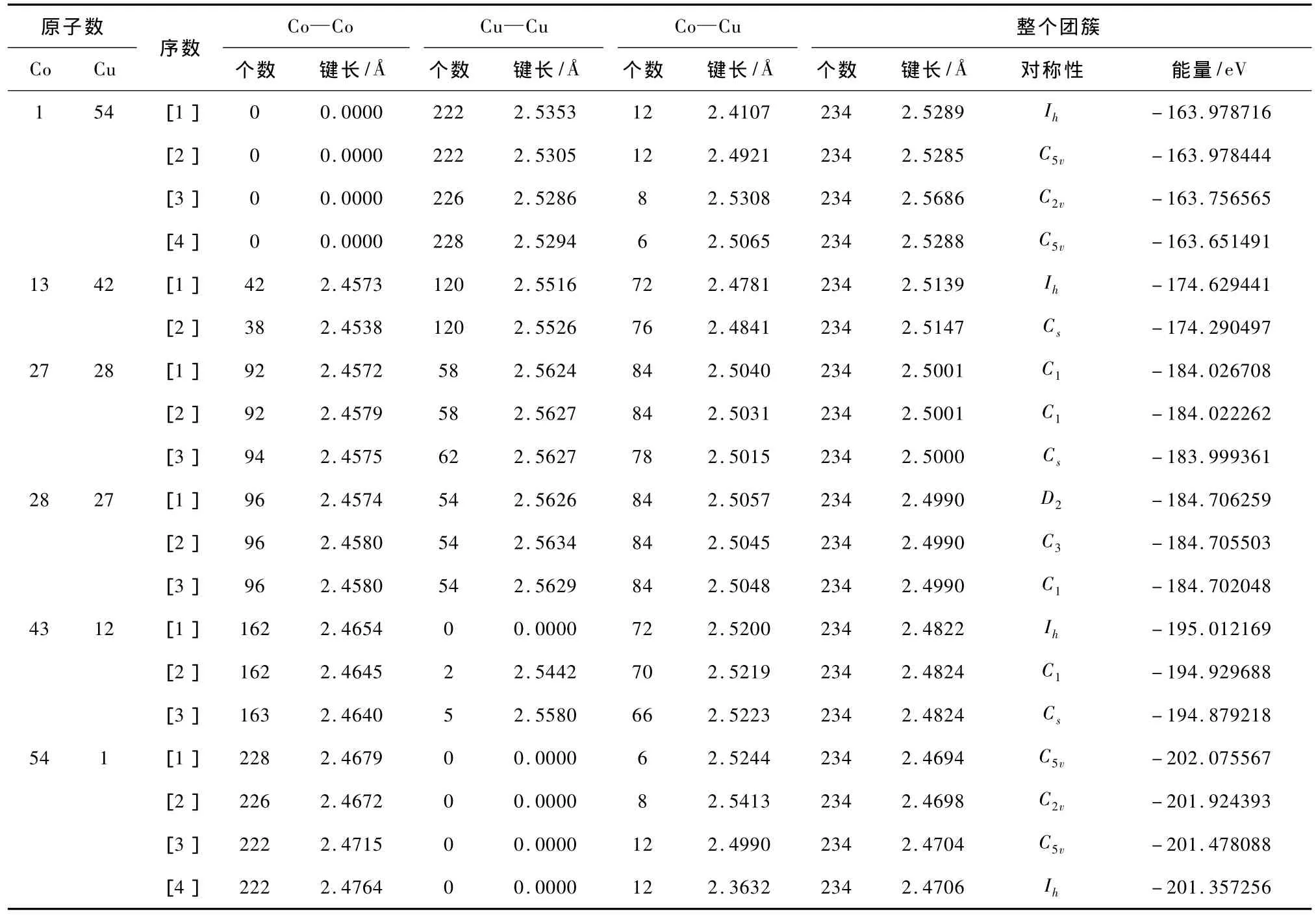
表2 Co1Cu54，Co13Cu42，Co27Cu28，Co28Cu27，Co43Cu12，Co54Cu1混合团簇基态及部分低激发态的各种键数、键长、对称性和能量

在Co1Cu54的基态结构中Co占据了中心位置，［2］，［3］，［4］中Co分别位于1V，2E，2V位置，拥有键能较大的Co-Cu键数最多的结构能量最低.很明显，在前两种结构中键能较大的Co—Cu键数是12，远大于后面的8和6，故前两种结构的能量低于后两种，［3］的能量也低于［4］.同时也发现前两个结构中团簇的各种键数相同，但［1］中键能较大的Co—Cu键的平均键长是2.4107，小于［2］中的2.4921，［1］的能量更低.

在组分Co13Cu42中，基态结构的13个Co原子位于团簇内部构成了具有Ih对称性的Mackay二十面体，42个Cu原子均匀覆盖在这个Mackay二十面体之上构成了具有Ih对称性的壳层结构.而［2］中的Co原子在没有完全替换位于1V位置上的Cu原子的情况下优先替换了第二壳层上的Cu原子从而极大的减少了键能最大的Co—Co键的数目，使整个团簇的能量升高.

Co27Cu28中有大量各种键数相同的结构，它们能量相差不足0.01 eV，但这微小的差异可能对研究这些团簇的性质产生一定的影响.在［1］和［2］中，都有13个Co原子位于内部，剩下的Co原子均位于2E位置.但仔细观察会发现位于2E位置上的Co原子的分布有所不同.［1］中2E位置上的Co原子连续分布，在最大化Co—Co键数的同时该键的平均键长也较短.同时我们还发现［3］的Co—Co键数是94多于前两种结构(92)，但其能量却比它们高.再观察能量次之的Co—Cu键，发现它的Co—Cu键比前两个团簇少了很多.可估算这两种键数分布的能差:ΔE≈2×3.15+4×2.58－6×2.80=－0.18 eV，故前两种结构的能量比第三种结构低.［3］在比［1］，［2］多两个Co—Co键和四个Cu—Cu键的同时，减少了6个Co—Cu键.换句话说，太多的能量最小的Cu—Cu键使得［3］不能拥有最低的能量.

Co28Cu27与Co27Cu28的分布相似，Co原子在替换完第一壳层上的Cu原子后再替换2E位置的Cu原子.由于在2E位置上Co原子分布的不同，Co28Cu27也有大量的各种键数相同、能量相差甚小的结构.前两种结构可以从Co—Co键的平均键长上看出［1］的能量较低.由于Co—Co键的平均键长相差很小，它们的能量也仅仅相差0.0008 eV.［2］与［3］相比，虽然Co—Co平均键长相同，但键能次之的Co—Cu键的平均键长却有差异，［2］稍小于［3］，因而其能量较低.

Co43Cu12的基态结构中，43个Co原子替换了团簇内部的13个Cu原子和2E位置上的30个Cu原子;［2］中有一个Co原子没有替换2E位置上的Cu原子反而替换了2V位置上的Cu原子;［3］是由于本应替换1V和2E位置上Cu原子的两个Co原子替换了2V位置上两个Cu原子而产生的.前两种结构的Co—Co键数虽然相同但［1］的Co—Cu键数比［2］多两个，［3］虽拥有最多数目的Co—Co键数(比前两个多一个)但其Co—Cu键数却比前两个团簇分别少6个和4个.

对于Co54Cu1，表2中相应的结构分别是指一个Cu原子位于2V，2E，1V及中心位置.基态结构拥有最多的Co—Co键数，它占优势的Co—Co键数完全可以弥补键能次之的Co—Cu键数的不足，虽然［4］拥有最高的Ih对称性但其较少的Co—Co键数决定着它不能成为基态.

通过计算发现:对于ConCu55－n(n=0—55)混合团簇，其基态结构主要由键能最大的Co—Co键数决定，同时还应考虑键能次之的Co—Cu键的数目;在各种键数相同的情况下Co—Co键的平均键长越短，其能量越低，若Co—Co键的平均键长也相同，则需对Co—Cu键的平均键长进行比较.这种方法没有精确的计算键能以及键之间的影响，但可以粗略的判断出两种结构能量的高低.

3.2. 能量及稳定性

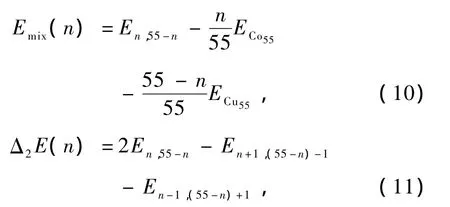
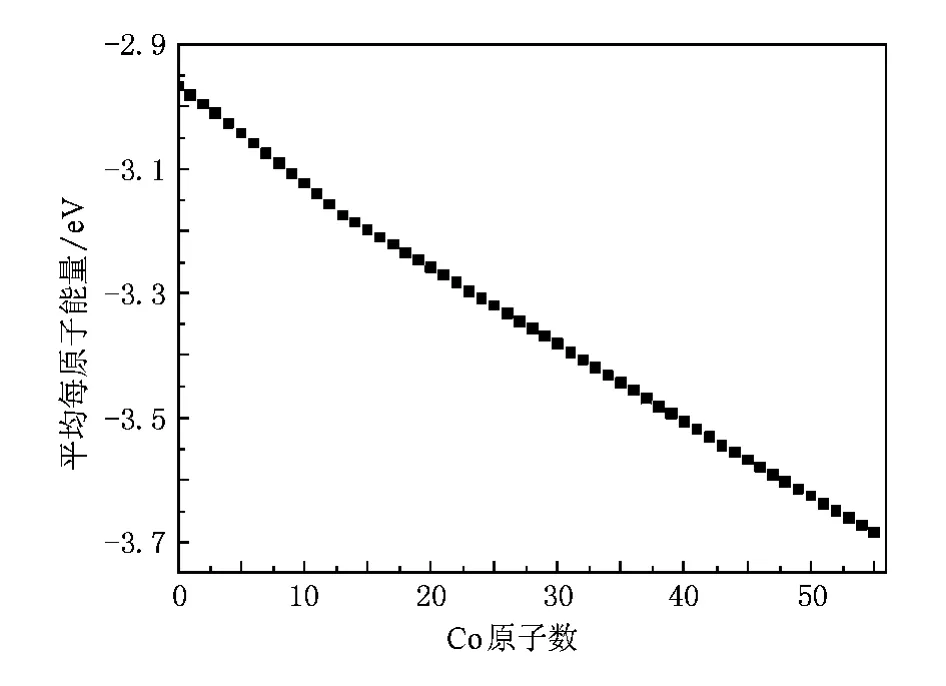
图5 ConCu55－n(n=0—55)混合团簇基态结构中平均每原子能量曲线

表3 ConCu55－n(n=0—55)混合团簇的基态能量和对称性

团簇的能量直接影响着团簇的稳定性，表3列出了ConCu55-n(n=0—55)混合团簇的基态能量和对称性，图5绘出了基态结构时平均每个原子的能量变化曲线.为了描述它们的稳定性，计算了这些混合团簇基态的混合能Emix(n)和二阶差分能Δ2E(n)，即Emix(n)越小说明该团簇的混合能越大，团簇越稳定，Δ2E(n)越小说明该团簇相对于邻近团簇而言越稳定.从图5中可以看出能量曲线在n等于13时发生明显的偏转.图6绘出了这些混合团簇基态结构的混合能、二阶差分能随Co原子数增加的变化曲线，可以看出混合能曲线呈V字形，二阶差分能除Co13Cu42外大体保持平衡，说明在ConCu55－n(n= 0—55)混合团簇中Co原子数在小于13和大于13时团簇的能量变化有很大的差异:Co原子数小于13时，Co原子位于团簇的内部，考虑到各种键之间的能差，尽可能同时使Co—Co，Co—Cu键的数目最大化、键长最小化的条件下Co原子替换相应位置的Cu原子.每当一个Co原子替换一个Cu原子时对整个团簇的能量影响很大(接近1 eV)，团簇的混合能迅速降低.当Co原子数等于13，即Co原子完全占据团簇内部时混合能和二阶差分能也达到了极值，团簇具有最稳定的结构.在Co原子数大于13以后Co原子替换一个Cu原子对整个团簇能量的影响明显减弱(约0.7 eV)，对混合能的影响也缓慢减小，直到Co原子数等于43.在这个过程中，Co原子在替换完内部的Cu原子后，依次、连续替换位于表面棱位置的Cu原子.Co原子数等于43时，Co原子恰好完全占据表面的棱位置，二阶差分能轻微向下突出，与邻近团簇相比其结构比较稳定，与此同时混合能也在此发生转变.Co原子大于43则替换位于表面顶点位置的Cu原子，虽然能量曲线(图5)没有明显的变化但混合能随Co原子数的增加迅速趋近于零.

图6 ConCu55－n(n=0—55)混合团簇基态结构的混合能(Emix)和二阶差分能(Δ2E)曲线

4. 结论

本文采用半经验的Gupta多体势结合遗传算法对ConCu55－n(n=0—55)混合团簇的基态结构及能量进行了研究和分析，结果显示:1)这些混合团簇的基态结构是在Co55，Cu55单质团簇的Mackay二十面体(Ih)结构基础之上发生的畸变.2)基态结构中两种原子基态质心间距呈波浪式变化，团簇中两种原子分离较多，混合较少.3)Co-Cu混合团簇的基态结构主要是由能量最大的Co—Co键数决定:基态结构应最大化Co—Co键数，同时也要考虑键能次之的Co-Cu键的数目，而且尽可能使这些键的平均键长最短;这些因素之间必须协调统一才能使整个团簇的能量最低.因此，从Cu55单质团簇开始，Co原子应该从中心到表面，从棱到顶点，依次、连续替换相应位置上的Cu原子.4)在这众多的混合团簇中Co13Cu42的稳定性最高，13个Co原子占据内部呈二十面体壳层结构，整个混合团簇完全处于分离状态.

感谢新疆大学物理科学与技术学院张蓓、陈楚老师的建议和讨论.

［1］Ruette F，González C 2002 Chem.Phys.Lett.359 428

［2］Wang J L，Zhao J J，Ding F，Shen W F，Lee H，Wang G H 2001 Solid State Commun.117 593

［3］Cheng D J，Huang S P，Wang W C 2006 Chem.Phys.330 423

［4］Deaven D M，Ho K M 1995 Phys.Rev.Lett.75 288

［5］Zeiri Y 1997 Comput.Phys.Commun.103 28

［6］Yang Q W，Zhu R Z 2005 Acta Phys.Sin.54 4245(in Chinese)［杨全文、朱如曾2005物理学报54 4245］

［7］Li G P，Zhang M L 2005 Acta Phys.Sin.54 2873(in Chinese)［李公平、张梅玲2005物理学报54 2873］

［8］Wang H Y，Li X B，Tang Y J，Chen X H，Wang C Y，Zhu Z H 2005 Acta Phys.Sin.54 3565(in Chinese)［王红艳、李喜波、唐永建、谌晓洪、王朝阳、朱正和2005物理学报54 3565］

［9］Wang Q L，Ge G X，Zhao W J，Lei X L，Yan Y L，Yang Z，Luo Y H 2007 Acta Phys.Sin.56 3219(in Chinese)［王清林、葛桂贤、赵文杰、雷雪玲、闫玉丽、杨致、罗有华2007物理学报56 3219］

［10］Grigoryan V G，Alamanova D，Springborg M 2006 Phys.Rev.B 73 115415

［11］Rodríguez-López J L，Aguilera-Granja F，Michaelian K，Vega A 2003 Phys.Rev.B 67 174413

［12］Ge Z G，Li G P，Pan X D 2008 Chin.Phys.B 17 3329

［13］Li G J，Wang Q，Li H T，Wang K，He J C 2008 Chin.Phys.B 17 3343

［14］Wu Z M，Wang X Q，Yang Y Y 2007 Chin.Phys.16 0405

［15］Ren F Z，Wang Y X，Zhang G B，Wei S K，Luo Y H 2009 Chin.Phys.B 18 1491

［16］Liu J T，Duan H M 2009 Acta Phys.Sin.58 4826(in Chinese)［刘建廷、段海明2009物理学报58 4826］

［17］Sondón T，Guevara J，Saúl A 2007 Phys.Rev.B 75 104426

［18］Feng C J，Xue Y H，Zhang X Y，Zhang X C 2009 Chin.Phys. B 18 1436

［19］Wang H Y，Li X B，Tang Y J，King R B，Schaefer H F 2007 Chin.Phys.16 1660

［20］Cleri F，Rosato V 1993 Phys.Rev.B 48 22

［21］Darby S，Mortimer-Jones T V，Johnston R L，Roberts C 2002 J. Chem.Phys.116 1536

［22］Mazzone G，Rosato V，Pintore M，Delogu F，Demontis P，Suffritti G B 1997 Phys.Rev.B 55 837

［23］Hristova E，Dong Y，Grigoryan V G，Springborg M 2008 J. Phys.Chem.A 112 7905

［24］Hristova E，Grigoryan V G，Springborg M 2008 J.Chem.Phys. 128 244513

［25］Cheng D，Huang S，Wang W 2006 Eur.Phys.J.D 39 41

［26］Zhang M，Fournier R 2006 J.Mol.Struct.762 49

［27］Hsu P J，Lai S K 2006 J.Chem.Phys.124 044711

PACC:7115Q，3640B

*Project supported by the National Natural Science Foundation of China(Grant No.10864005)，the Scientific Research Starting Foundation for Returned Overseas Chinese Scholars，Ministry of Education，China.

†Corresponding author.E-mail:dhm@xju.edu.cn

Study of the structure evolution and ground state energy of ConCu55－n(n=0—55)bimetallic clusters by using the Gupta potential combined with a genetic algorithm*

E Xiao-Liang Duan Hai-Ming†
(College of Physical Science and Technology，Xinjiang University，Urumqi830046，China)
(Received 13 September 2009;revised manuscript received 3 December 2009)

The ground-state structures and energies of the bimetallic clusters ConCu55－n(n=0—55)were obtained by using the semi-empirical Gupta potential combined with a genetic algorithm.The ground-state geometries of those bimetallic clusters can be characterized by the basicMackay icosahedron of the pure Co55(Cu55)cluster.Beginning with n=0(Cu55)，the Cu atom(s)is(are)replaced in order and continuously by the Co atom(s)from the center to the surface and from the edge to the vertex.The ground-state structure depends on the number of the Co—Co bonds which have the largest energy，the number of the Co-Cu bonds with large energy and the average bond length of those bonds.Co13Cu42is a magic cluster with an icosahedral core formed by 13 Co atoms，which plays a key role in the high stability of those bimetallic clusters.

clusters，structure and energy，Gupta potential，genetic algorithm

book=477,ebook=477

*国家自然科学基金(批准号:10864005)，教育部留学回国人员科研启动基金资助的课题.

†通讯联系人.E-mail:dhm@xju.edu.cn