Cs2NaMF6(M=Al，Ga):Cr3+络合分子体系局域结构和基态分裂的理论研究*

王利霞 邝小渝李慧芳 柴瑞鹏 王怀谦

(四川大学原子与分子物理研究所，成都610065)

(2009年12月14日收到;2010年1月17日收到修改稿)

Cs2NaMF6(M=Al，Ga):Cr3+络合分子体系局域结构和基态分裂的理论研究*

王利霞 邝小渝†李慧芳 柴瑞鹏 王怀谦

(四川大学原子与分子物理研究所，成都610065)

(2009年12月14日收到;2010年1月17日收到修改稿)

采用双自旋轨道耦合系数模型并结合完全能量矩阵的方法对Cs2NaMF6(M=Al，Ga):Cr3+体系中Cr3+离子的基态分裂和局域结构进行了研究.通过模拟光谱和EPR谱确定了Cr3+取代M3+形成的两种占位结构的畸变角，发现用双自旋轨道耦合系数模型与单自旋轨道耦合系数模型计算出的畸变角Δθ存在较大的差异.这表明在研究氟化物络合分子的能级精细结构和局域结构畸变时，配体F－离子对体系的自旋轨道耦合机理的影响是不可忽略的.同时，讨论了EPR参量D随夹角θ、平均参量ζ1以及偏离参量ζ2的变化规律.

Cs2NaMF6(M=Al，Ga):Cr3+体系，双自旋轨道耦合系数模型，完全能量矩阵

PACC:7170C，7630，7630F

1. 引言

Cs2NaMF6(M=Al，Ga)晶体具有六角钾冰晶石结构，在掺杂Cr3+离子后Cs2NaMF6(M=Al，Ga): Cr3+体系作为一类新型的固体激光材料而受到人们的广泛关注［1—7］.X射线与中子衍射等实验都证实在Cs2NaMF6(M=Al，Ga)体系中M3+离子存在两种不同的占位结构［8，9］，Cr3+离子掺入后将取代M3+离子形成(CrF6)3－络合团簇，其局域结构为D3d点群对称［1，10，11］.由于掺杂离子与被取代离子的半径存在一定的差异，因此处于Cs2NaMF6(M=Al，Ga): Cr3+体系中的(CrF6)3－络合团簇相对于原晶体中(MF6)3－团簇的晶体结构将会发生畸变.研究这种畸变的形成机理和大小是固体波谱学中一类基础性课题.目前对于过渡金属在固体中形成络合团簇所产生的光谱和局域结构畸变的研究主要采用高阶微扰和完全能量矩阵这两种方法，其中对于自旋轨道耦合相互作用的处理亦有单自旋轨道耦合系数和双自旋轨道耦合系数这两种物理模型.本文将在双自旋轨道耦合系数模型的基础上采用完全能量矩阵的方法对Cs2NaMF6(M=Al，Ga):Cr3+体系的光谱，基态零场分裂和局域结构展开系统的研究，并通过与单自旋轨道耦合系数模型计算结果的对比分析，将证实即使是对于像氟化物这样典型的离子型晶体而言，配体离子F－对于过渡金属中心离子的自旋轨道耦合作用机理的贡献依然是重要的，它将明显影响到局域晶格结构畸变角Δθ的计算结果.

2. 理论方法

2.1. 双自旋轨道耦合系数模型

Sugano等人指出:从d轨道强场基出发，在考虑到eg和t2g两个子轨道的差异以及它们与近邻配体之间形成的共价效应影响后，一般而言对处于络合物中的过渡金属离子d轨道内电子的自旋轨道耦合相互作用机理的描述需要引入两个不同的自旋轨道耦合系数ζ和ζ′，定义如下［12］:

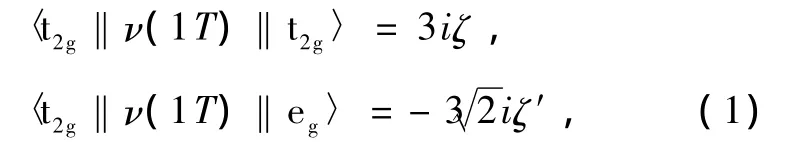
其中ζ和ζ′可表示为［12—14］

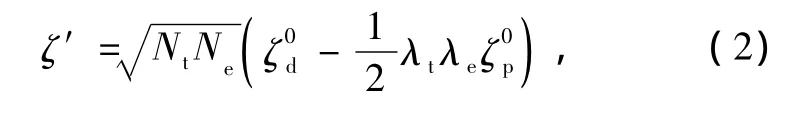
ζ0d和ζ0p分别是中心金属离子的d电子和配体的p电子的自旋轨道耦合系数.相应的分子轨道波函数为［15］

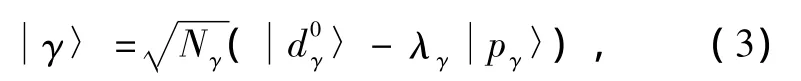
和归一化条件［15］

其中的群重叠积分Sdp(γ)可由径向波函数算出，fγ值用近似关系fγ≈(B/B0+C/C0)/2并利用光谱参量B，C的实验值确定;B0，C0是自由离子参量.对于F－离子ζ0p=220cm－1［15］，Cr3+离子ζ0d=273cm－1，B0=1030cm－1，C0=3850cm－1［16］.从(2)，(4)，(5)式中，可以算出Cs2NaMF6(M=Al，Ga):Cr3+体系中Cr3+离子分别处在两种不同占位情况下Nγ，λγ，ζ，ζ′参量的值.

2.2. d3组态离子的完全能量矩阵

对于d3组态离子的120个微观状态j(j=1，

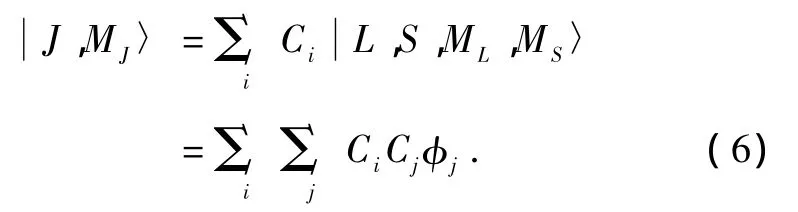
这里Ci，Cj是Clebsch-Gordon系数.描述三角晶体场中的dn组态离子的相互作用哈密顿量如下:

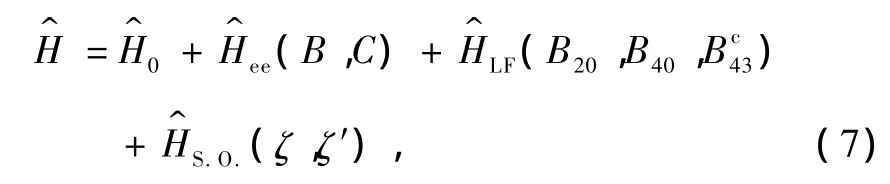
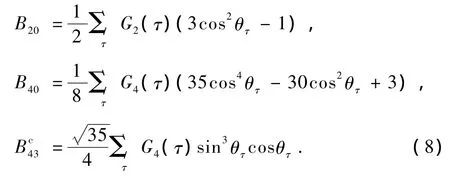
其中的晶体场强度参量G4(τ)由光谱确定.S.O.涉及ζ和ζ′两个参量［19］.为使物理图像清晰和方便分析对比，引入平均参量ζ1和偏离参量ζ2如下:

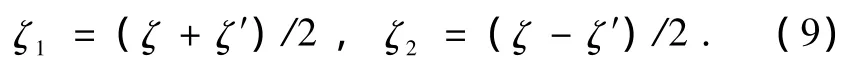
在ζ2=0的极限情况下，双自旋轨道耦合系数模型将自动退化成单自旋轨道耦合系数模型.因此，我们可以说双自旋轨道耦合系数模型是一种物理内涵更丰富的模型.

2.3. d3组态离子的EPR参量

描述三角晶体场中Cr3+离子4A2(S=3/2)基态EPR谱的自旋哈密顿量如下［20］:

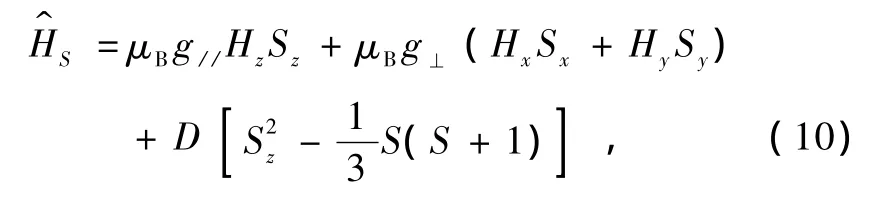
前两项代表外磁场的作用，第三项代表磁场为零时基态的能级结构，D是零场分裂参量.由(10)式可求得零磁场下基态4A2(S=3/2)的能级

相应的分裂能ΔE表示为

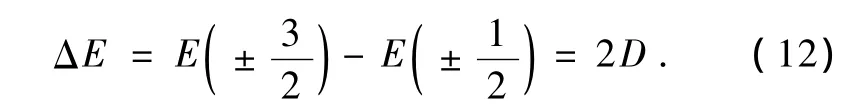
采用完全能量矩阵的对角化计算并结合(8)式和(12)式，可建立起络合分子局域结构参量与光谱和EPR谱之间的联系，并通过模拟光谱和EPR参量D来分析掺杂过渡金属络合分子局域结构畸变的规律.下面运用这一方法对氟化物Cs2NaMF6(M =Al，Ga):Cr3+体系进行具体的研究.

3. 计算与分析

3.1. Cs2NaMF6(M=Al，Ga):Cr3+体系局域晶格结构参量的计算

在Cs2NaMF6(M=Al，Ga)晶体中M3+离子存在两种不同的占位，记为M1和M2，M3+离子六个最邻近F－配体构成的八面体沿C3轴畸变形成D3d点群对称.对Cs2NaAlF6的M1占位，其Al—F键长R0和C3轴与Al—F键的夹角θ0分别为R0=1.820，θ0=55.0°，对M2占位R0=1.813，θ0=53.3°［1，21］;而对Cs2NaGaF6的M1占位R0=1.901，θ0= 55.2°，对M2占位R0=1.902，θ0=53.2°［1，10］.当体系掺入Cr3+离子后，Cr3+离子将取代原晶格中的M3+离子形成局域的(CrF6)3－团簇(如图1).由于掺入Cr3+离子半径不同于原晶格中的M3+离子，故(CrF6)3－团簇中的键长R和夹角θ都将发生畸变.即

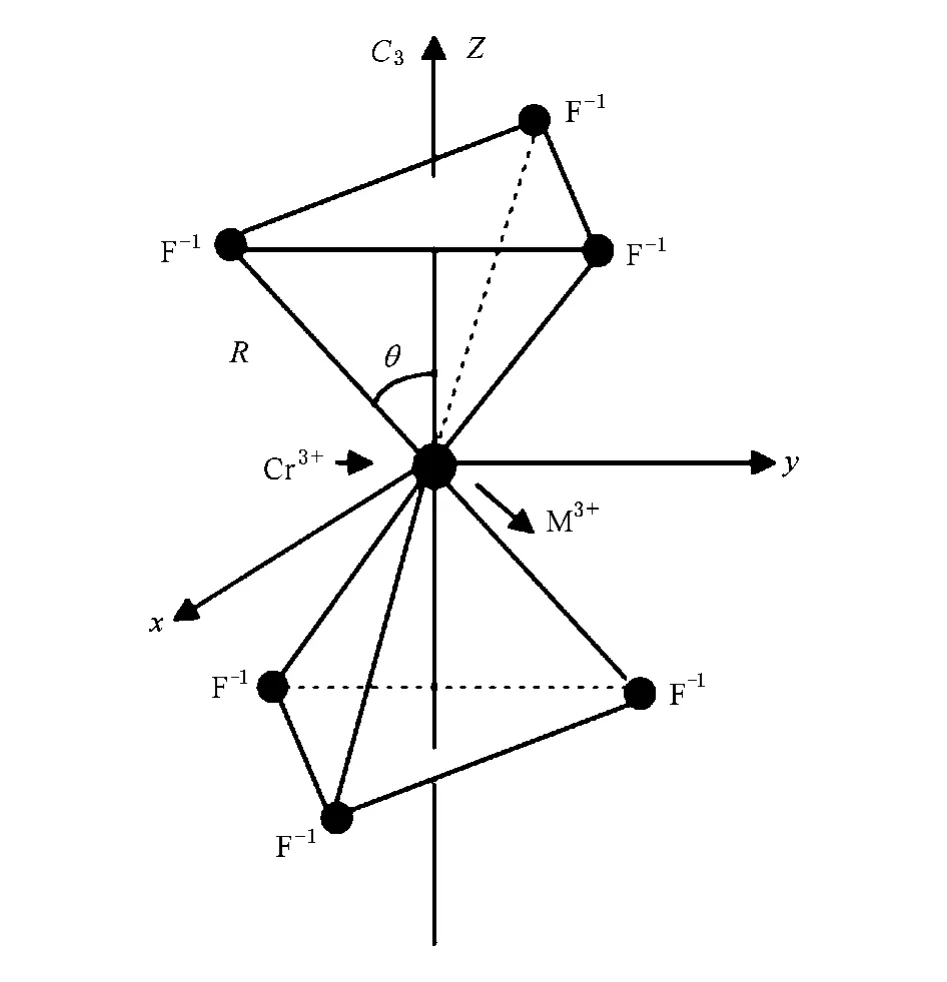
图1 Cs2NaMF6(M=Al，Ga):Cr3+体系中(CrF6)3－团簇的局域结构(R是Cr—F键长，θ是Cr—F键与C3轴之间的夹角)

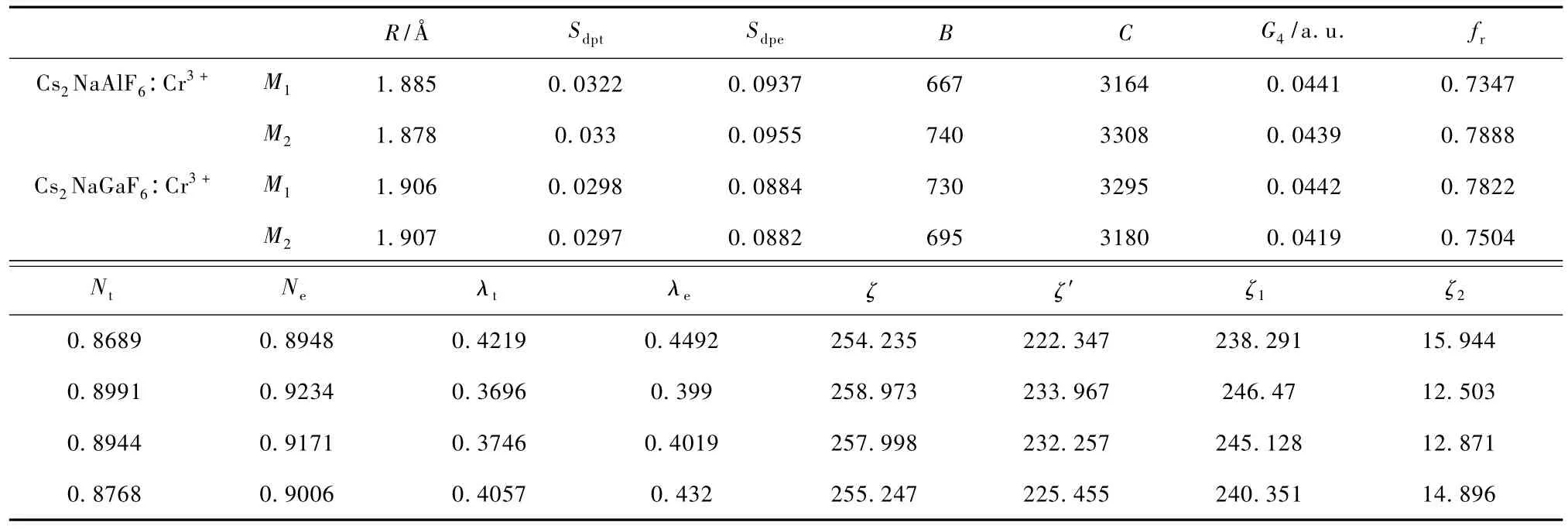
表1 Cs2NaMF6(M=Al，Ga):Cr3+体系的Cr—F键长，群重叠积分，Racah参量，归一化系数，轨道混合系数，自旋轨道耦合系数，平均参量和偏离参量(单位:cm－1)

表2 在T=20K，ζ=ζ′=0时，Cs2NaMF6(M=Al，Ga):Cr3+体系在M1和M2位置处的光谱(所有量均以cm－1为单位)

表3 由不同模型计算得到的Cs2NaMF6(M=Al，Ga):Cr3+体系的畸变角和EPR参量D

3.2. EPR参量D随键角θ的变化规律

根据前人及我们的前期工作可知EPR参量D非常敏感的依赖于晶体结构中的角度变量θ.已发表的单自旋轨道耦合系数模型的计算结果表明:当络合分子体系的对称性为严格Oh群时，亦即θ= θoh(θoh=arccos(1))时，相应的EPR参量D= 0，这意味着Cr3+离子的基态这时依然保持着四重简并度［28］.为展示出双自旋轨道耦合系数模型下Cr3+离子基态分裂参量D随θ角的变化规律，同时与单自旋轨道耦合系数模型的计算结果进行对比，在不失普遍性的前提下我们取Cs2NaAlF6:Cr3+的M1占位参量来描绘EPR参量D随θ的变化曲线.具体计算包括ζ2>0，ζ2=0，ζ2<0三种情况，θ角的取值范围为θ=θoh±6°，详细的结果如图2所示.单自旋轨道耦合系数模型对应于ζ2=0的曲线，该曲线在θ=θoh时D值严格为零，而此时对ζ2>0有D<0，对ζ2<0有D>0.三条曲线的交点大约在θp=56.7356°.对于(CrF6)3－团簇实际计算出的ζ2值属于ζ2>0的情况，且EPR参量D随θ的增大而减小，并在θ=θoh±1°范围内呈近似线性关系.由于Cs2NaMF6(M=Al，Ga):Cr3+体系中(CrF6)3－团簇的θ值都小于θp，故对于(CrF6)3－团簇采用双自旋轨道耦合系数模型计算出的夹角θ都将小于单自旋轨道耦合系数模型的计算结果.这一点在表3列出的两种模型计算结果的对比中得到了清楚的展现.

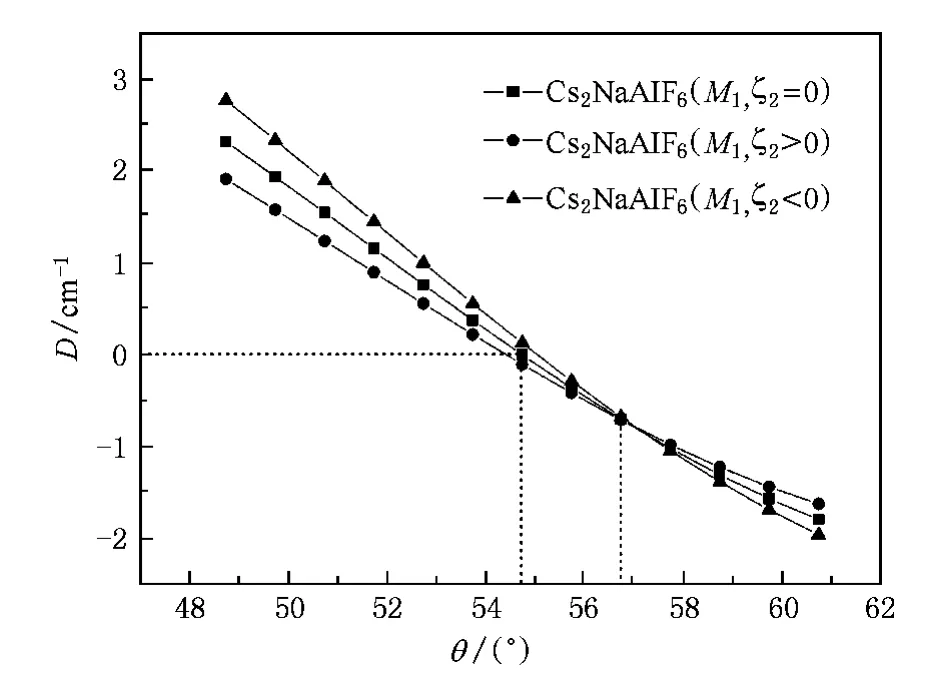
图2 在ζ2>0，ζ2=0，ζ2<0三种情况下Cs2NaAlF6:Cr3+的M1占位处EPR参量D随Cr—F键与C3轴之间夹角θ的变化关系曲线

3.3. EPR参量D随平均参量ζ1和偏离参量ζ2的变化规律

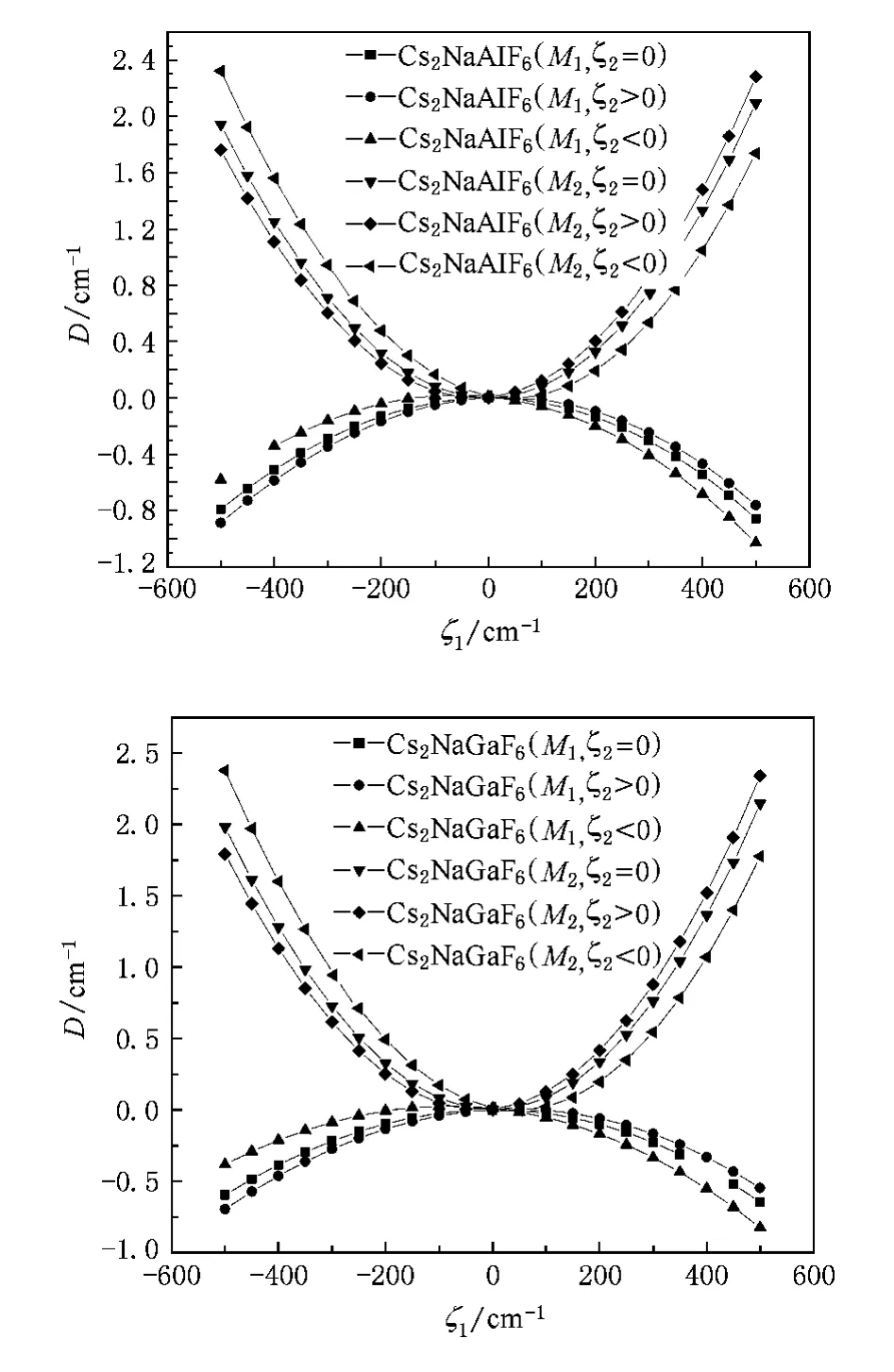
图3 在ζ2>0，ζ2=0，ζ2<0三种情况下Cs2NaMF6(M=Al，Ga):Cr3+体系的EPR参量D与平均参量ζ1的关系曲线

以3.1中定出的Cs2NaMF6(M=Al，Ga):Cr3+体系的参量为基础，通过完全对角化矩阵的计算来描绘EPR参量D随变量ζ1和ζ2的变化曲线. D(ζ1)曲线和D(ζ2)曲线分别针对M1和M2两种占位进行，具体结果绘于图3和图4.我们看到，D(ζ1)曲线并非严格的偶次方函数关系，对于M1占位D(ζ1)曲线开口向下，而对于M2占位D(ζ1)曲线开口向上.其物理原因可归因于M1占位的夹角θ大于正八面体时的夹角θoh，即θ(M1)>θoh，导致体系的EPR参量D<0，而M2占位正好相反，有θ(M2)<θoh，导致体系的EPR参量D>0.图3说明(CrF6)3－团簇的基态分裂D(ζ1)曲线开口方向与局域晶格结构的畸变方向之间存在着对应关系.图4的D(ζ2)曲线显示出EPR参量D随ζ2的增大而减小的趋势，在ζ2=－40—40cm－1的范围内，我们注意到D与ζ2呈近似线性关系.

图4 Cs2NaMF6(M=Al，Ga):Cr3+体系的EPR参量D与偏离参量ζ2的关系曲线

4. 结论

运用双自旋轨道耦合系数模型并结合对角化完全能量矩阵的方法，我们研究了Cs2NaMF6(M= Al，Ga):Cr3+体系的局域结构，EPR参量D随夹角θ以及平均参量ζ1和偏离参量ζ2的变化规律.我们发现对于Cs2NaMF6(M=Al，Ga):Cr3+体系中的(CrF6)3－团簇的局域晶格结构用双自旋轨道耦合系数模型与单自旋轨道耦合系数模型算出的畸变角Δθ存在较大的差异.这说明配体F－的自旋轨道耦合相互作用通过共价效应对Cs2NaMF6(M=Al，Ga):Cr3+体系中络合离子(CrF6)3－基态分裂的影响是不可忽略的.本文的分析方法可应用于其他的过渡金属络合分子体系.

［1］Vrielinck H，Loncke F，Callens F，Matthys P 2004 Phys.Rev. B 70 144111

［2］Agate B，Rafailov E U，Sibbett W，Saltiel S M，Battle P，Fry T，Noonan E 2003 Opt.Lett.28 1963

［3］Keller U 2003 Nature 424 831

［4］Sosman L P，Tavares Jr A D，Da Fonseca R J M，Abritta T，Khaidukov N M 2000 Solid State Commun.114 661

［5］Da Fonseca R J M，Tavares Jr A D，Silva P S，Abritta T，Khaidukov N M 1999 Solid State Commun.110 519

［6］Fargin E，Lestienne B，Dance J M 1990 Solid State Commun. 75 769

［7］Vrielinck H，Khaidukov N M，Callens F，Matthys P 2002 Radiat.Eff.Defects Solids 157 1155

［8］Pueyo L，Richardson J W 1977 J.Chem.Phys.67 3583

［9］Knox K 1960 Acta Cryst.13 507

［10］Bordallo H N，Wang X，Hanif K M，Strouse G F，Da Fonseca R J M，Sosman L P，Tavares Jr A D，2002 J.Phys.:Condens. Matter 14 12383

［11］Babel D，Haegele R，Pausewang G，Wall F 1973 Mater.Res. Bull.8 1371

［12］Sugano S，Tanabe Y，Kamimura H 1970 Multiplets of Transition Metal Ions in Crystals(New York:Academic)

［13］Curie D，Barthon C，B Canny 1974 J.Chem.Phys.61 3048

［14］Zhao M G，Xu J A，Bai G R，Xie H S 1983 Phys.Rev.B 27 1516

［15］Du M L，Rudowicz C 1992 Phys.Rev.B 46 8974

［16］Griffith J S 1964 Theory of Transition-Metal Ions(London: Cambridge University press)

［17］Slater J C 1960 Quantum Theory of Atomic Structure(New York: McGraw－Hill)

［18］Newman D J，Urban W 1975 Adv.Phys.24 793

［19］Li F Z，Zhou Y Y 1998 Acta Phys.Sin.47 472(in Chinese)［李福珍、周一阳1998物理学报47 472］

［20］Abragam A，Bleaney B 1970 Electron Paramagnetic Resonance of Transition Ions(New York:Oxford University Press)

［21］Bordallo H N，Henning R W，Sosman L P，Da Fonseca R J M，Tavares Jr A D，Hanif K M，Strouse G F 2001 J.Chem.Phys. 115 4300

［22］Zheng W C 1995 Phys.B 215 255

［23］Li Z M，Shuen W L 1996 J.Phys.Chem.Solids 57 1673

［24］Cao X Z，Song T Y，Wang X Q 1997 Inorganic Chemistry (Beijing:Higher Education Press)(in Chinese)［曹锡章、宋天佑、王杏乔1997无机化学(北京:高等教育出版社)］

［25］Clementi E，Raimondi D L 1963 J.Chem.Phys.38 2686

［26］Clementi E，Raimondi D L，Reinhardt W P 1967 J.Chem. Phys.47 1300

［27］Huang J L，Kuang X Y，Li Y 2008 Chem.Phys.Lett.458 227

［28］Wei Q，Yang Z Y，Wang C J，Xu Q M 2007 Acta Phys.Sin.56 507(in Chinese)［魏群、杨子元、王参军、许启明1997物理学报56 507］

PACC:7170C，7630，7630F

*Project supported by the National Natural Science Foundation of China(Grant Nos.10774103，10974138).

†Corresponding author.E-mail:scu_kuang@163.com

Theoretical study of local structure and ground-state splitting of Cs2NaMF6(M=Al，Ga):Cr3+complex molecule systems*

Wang Li-Xia Kuang Xiao-Yu†Li Hui-Fang Chai Rui-Peng Wang Huai-Qian
(Institute of Atomic and Molecular Physics，Sichuan University，Chengdu610065，China)
(Received 14 December 2009;revised manuscript received 17 January 2010)

Based on the two spin orbit coupling parameter model and the complete energy matrices for a d3configuration ion in a trigonal ligand field，the local structure and the ground-state splitting of Cr3+ion in Cs2NaMF6(M=Al，Ga):Cr3+systems have been studied.By simulating the EPR parameter D and the optical spectra，the distorted angles of two inequivalent sites formed by Cr3+replacing M3+are determined and the obvious difference of the distorted angles Δθ calculated by using two spin orbit coupling parameter model and single spin orbit coupling parameter model is found.Our results indicate that the influence of ligand F-can not be ignored with respect to spin orbit coupling mechanism when the energy level fine structure and local structure distortion of fluoride complex molecules are studied.Meanwhile，the dependence of EPR parameter D on angle θ，average parameter ζ1and divergent parameter ζ2is discussed，respectively.

Cs2NaMF6(M=Al，Ga):Cr3+systems，two spin orbit coupling parameter model，complete energy matrix

book=560,ebook=560

*国家自然科学基金(批准号:10774103，10974138)资助的课题.

†通讯联系人.E-mail:scu_kuang@163.com