山区急倾斜煤层开采上覆岩层弯曲挠度预计

李辉，梁冰，李刚，白云鹏，张春梅

(1.辽宁工程技术大学力学与工程学院，辽宁阜新 123000; 2.辽宁工程技术大学安全科学与工程学院，辽宁阜新 123000)

山区急倾斜煤层开采上覆岩层弯曲挠度预计

李辉1，梁冰1，李刚2，白云鹏1，张春梅1

(1.辽宁工程技术大学力学与工程学院，辽宁阜新 123000; 2.辽宁工程技术大学安全科学与工程学院，辽宁阜新 123000)

为了研究山区急倾斜煤层开采上覆岩层的弯曲变形规律，建立了上覆岩层弯曲变形的力学模型，运用弹性力学中的薄板弯曲理论，推导了上覆岩层弯曲挠度的预计公式，利用此公式对上覆岩层的弯曲挠度进行了计算。研究结果表明:(1)由于山区急倾斜煤层覆岩的线性荷载的作用，岩板的弯曲挠度曲线不再具有对称性，岩板弯曲挠度的最大值偏向于岩板倾斜的下山方向;(2)岩板弯曲挠度随着采深的增大而增大，岩板弯曲挠度最大值出现的位置逐渐由下山方向向采空区中点移动，但是最大挠度出现的位置不会越过采空区中点而位于倾斜岩板的上山方向;(3)岩板弯曲挠度随着山地倾角的增大而增大，岩板挠度最大值出现的位置距离采空区中点越来越远;(4)岩板弯曲挠度随着煤层倾角的增大而减小，岩板弯曲挠度最大值出现的位置距离采空区中点越来越远。

山区;急倾斜煤层;薄板弯曲理论;弯曲挠度;上覆岩层

0 引言

我国煤炭资源的分布十分广泛，平原、丘陵和山区的地下都蕴藏着丰富的煤炭资源，急倾斜煤炭储量占我国煤炭储量的15%～20%［1］，我国的西部矿区50%以上的矿井开采的是位于山区覆盖下的急倾斜煤层。山区急倾斜煤层开采上覆岩层的弯曲变形规律的研究，有利于我国西部矿区顶板的管理，对促进我国煤炭工业的发展和保证我国西部能源战略计划的实施具有重大的现实意义和深远的社会意义［2］。

1 挠度曲线不对称的原因分析

水平和近水平开采时，上覆岩层的弯曲挠度曲线具有对称性，且以通过采空区中点的铅垂线为对称轴。在山地条件下开采急倾斜煤层时，上覆岩层的弯曲挠度曲线不再具有对称性，造成这种不对称性的两个主要因素为:(1)山区地形所产生的不均匀荷载和倾斜岩层上方所产生的不均匀荷载;(2)由于岩层本身是倾斜的，所以作用在岩层上面的荷载又可分为沿着岩层法向方向的荷载和沿着岩层倾斜方向的荷载。

2 岩板弯曲变形力学模型的建立

水平煤层开采上覆岩层只受到竖向荷载和自重力的作用，采空区上方的岩层通过组合梁(板)将重力荷载传到两侧的支座上，形成岩体的平稳下沉。当附加应力超过岩石强度极限时，直接顶板便断裂而冒落，岩体将发生变形，产生位移。当跨落的岩体尺寸小于开采空间时，岩体可以在开采空间内自由移动，这部分岩体构成了水平煤层开采的跨落带，称为“下位岩层”。跨落带上方的岩层由于尺寸大于下落空间，这部分岩块会平稳地下沉，而且保持层状沿法向方向弯曲，形成整体移动带，称为“上位岩层”［1］。

对于急倾斜煤层开采引起的岩层移动，也可以把上覆岩层分为直接顶板、下位岩层和上位岩层，上位岩层易产生变形和整体弯曲，但同下位岩层相比，岩层的变形程度明显要小，属于小变形区，上位岩层的分层特征和整体性保持完好［1］。老顶位于直接顶之上。它一般在直接顶跨落后，长时期内都不易自行跨落，往往只发生缓慢变形、下沉［3］。本文研究的是老顶的弯曲挠度预计。

在弹性力学中，对梁、板、圆筒等的计算都有严格的要求和实用范围［4］。板的厚度t与板面最小尺寸之比在1/100～1/5的平面板可以定义为薄板，对于脆性较大的硬岩，将岩板定义为薄板的几何条件可以适当的放宽［5］。此外，岩板的挠度必然不大于煤层的开采厚度，而岩板的自身厚度又往往大于煤层开采的厚度，故岩板的挠度必然远小于自身厚度，这符合薄板弯曲小挠度理论的前提条件。因此，上位岩层(老顶)选择弹性力学中的薄板弯曲模式是可行的。建立山区急倾斜煤层开采的简化模型如图1。

图1 山区急倾斜煤层开采岩板受力图Fig.1 the free body diagram of rock plate of steeply-inclined seam mining in mountainous

在图1中，ABCD为所要研究的岩板(老顶)，楔形体GHIJKL为简化后的山地地形，楔形体ABCDEF为倾斜岩板ABCD上的岩体。长方体CDEF-GHIJ对岩板ABCD构成均匀分布的载荷q1，楔形体ABCDEF 和GHIJKL对岩板构成沿着岩板倾斜方向线性变化的不均匀荷载q2和q3。由于岩板ABCD具有一定的倾斜角度，所以q1、q2和q3在岩板ABCD上又分解为沿着岩板法线方向的横向载荷q11、q21和q31，以及沿着岩板倾斜方向的纵向荷载q12、q22和q32。横向荷载q11、q21和q31，对岩板的弯曲起着主要的作用，而纵向荷载q12、q22和q32单独作用时，岩板不会产生横向挠度，只有在横向荷载q11、q21和q31的作用下已经产生一定的挠度时，才对岩板的横向挠度有一个加大的作用。由前人的研究成果可知［6］，纵向荷载q12、q22和q32虽然对岩板的横向挠度有加大的作用，但是纵向荷载所产生的挠度很小，在精度要求不高的弯曲挠度预计中可以忽略。因此，本文在预计岩板的弯曲挠度时，只考虑了横向荷载q11、q21和q31的作用。

3 岩板弯曲挠度的理论计算

根据图1中给出的条件，运用材料力学中的斜截面上的应力公式［7］，求得横向荷载q11=Hγcos2θ;q21=hγ(y/b)cosθ;q31=h1γ(b－y/b)cos2θ，其中h= bsinθ，h1=bcosθtanφ

由弹性力学中的薄板弯曲理论可知［8］，薄板在只有横向荷载作用时的挠曲微分方程为:

式中:D为薄板的弯曲刚度，E是薄板的弹性模量，δ是薄板的厚度，μ是泊松比，ω是挠曲函数，q是薄板上所受的横向荷载。

运用薄板弯曲挠度的叠加理论，图1中岩板ABCD的总挠度可以看成是q11产生的挠度ω1、q21产生的挠度ω2和q31产生的挠度ω3的叠加。即ω总= ω1+ω2+ω3。

假定薄板的边界条件为四边简支，上述模型中，在横向荷载q11、q21和q31作用下，薄板的挠曲微分方程和边界条件可以表示如下:

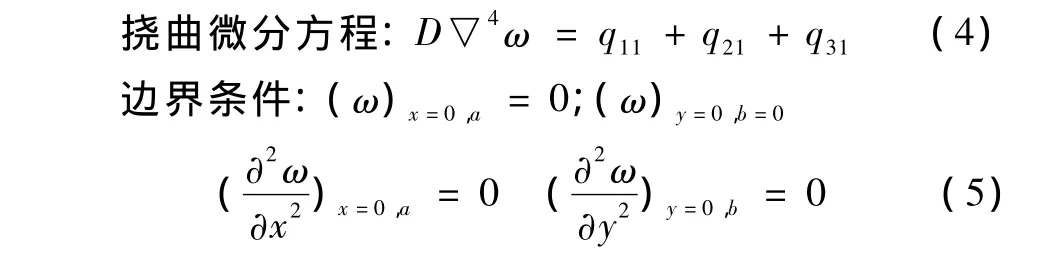
纳维把挠度ω的表达式取为如下的重三角级数，求得了重三角级数解，即:

其中，m和n是正整数，显然满足式(5)的所有边界条件。

把等式右边的q=q(x，y)展为重三角级数:

由傅里叶级数的系数展开公式得出:

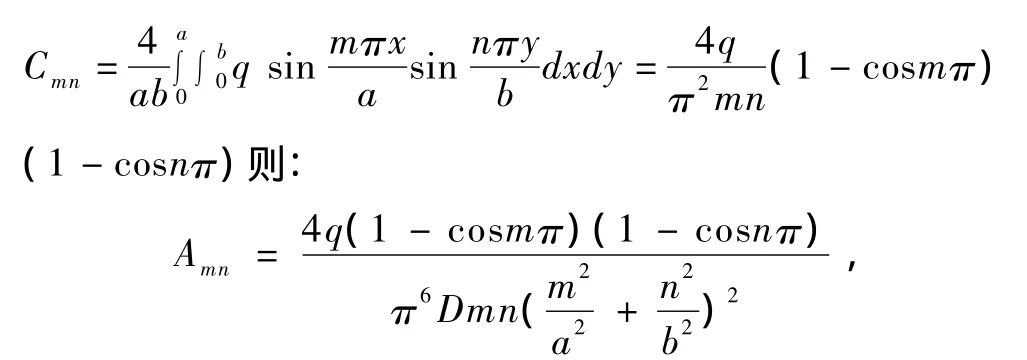
其中m和n是正整数。从而得到岩板的弯曲挠度计算公式为:

求ω对y的一阶偏导数，并使其等于0，可得到在x=a/2的直线上，将出现ω的最大值。

4 算例分析

某矿急倾斜工作面埋深100m，煤层倾角60°，工作面斜长120m，工作面宽80m，老顶厚度12m，山地倾斜方向与煤层倾斜方向一致，山地倾斜角度45°。即:H=100m，a=80m，b=120m，δ=12m，θ=60°，φ= 45°。取E=25×103MPa，γ=25kN/m3，μ=0.25，计算最大挠度弯曲时，取x=a/2。沿采空区中部，计算岩板的弯曲挠度时取m=1，n=1，2进行计算，计算数据如表1所示。

图2 岩板弯曲挠度曲线图Fig.2 Curves of bending deflection

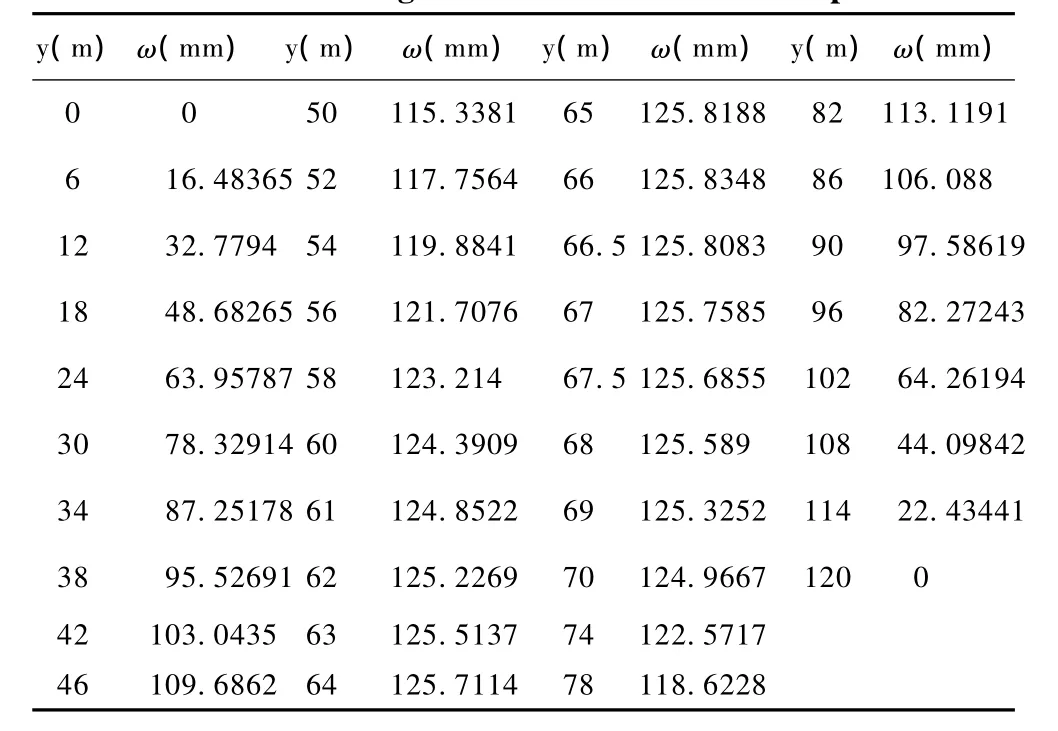
表1 倾斜岩板弯曲挠度值Table 1 Bending deflections of tilted rock plates

从表1中可以看出，y=60m时，ω=124.39mm，而弯曲挠度最大值出现的位置为y=66m处，最大弯曲挠度为125.83mm，并且y=70m处的弯曲挠度值仍然大于采空区中点的弯曲挠度值。

图3 采深不同时的岩板弯曲挠度曲线Fig.3 Curves of bending deflection in defferent mining depths

图4 山地的倾角不同时岩板的弯曲挠度曲线Fig.4 Curves of bending deflection in defferent inclination angles of mountainous area

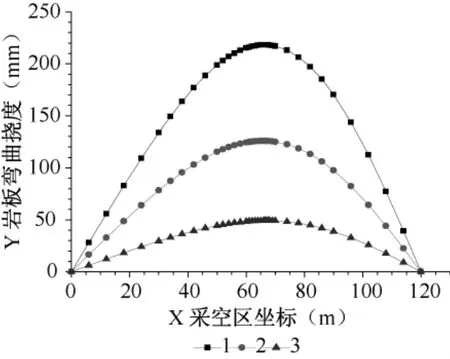
图5 煤层倾角不同时的岩板弯曲挠度曲线Fig.5 Curve of bending deflection in defferent inclination angles of coal seam

5 弯曲挠度的影响因素分析

图2可看出，由于山区急倾斜煤层覆岩的线性荷载的作用，岩板的弯曲挠度曲线不再具有对称性，岩板弯曲挠度的最大值偏向于岩板倾斜的下山方向。

5.1 采深的影响

从图3中可以看出，岩板弯曲挠度随着采深的增大而增大，岩板弯曲挠度最大值出现的位置逐渐由下山方向，向采空区中点移动，但是最大挠度出现的位置不会越过采空区中点而位于倾斜岩板的上山方向。

5.2 山地倾角的影响

从图4中可以看出，随着山地倾角的增大，岩板弯曲挠度逐渐增大，并且岩板挠度最大值出现的位置距离采空区中点越来越远，山地倾角为15°时，弯曲挠度最大值出现在65m处;山地倾角为75°时，弯曲挠度最大值出现在67m处。

5.3 煤层倾角的影响

从图5中可以看出，随着煤层倾角的增大，岩板弯曲挠度逐渐减小，岩板弯曲挠度最大值出现的位置距离采空区中点越来越远。

6 结论

本文运用薄板理论，推导出山区急倾斜煤层开采时，上覆岩层的弯曲挠度计算公式。计算出采深不同、山地倾角不同和煤层倾角不同时，上覆岩层的弯曲挠度，并且绘制出弯曲挠度曲线图。最后得出采深、山地倾角和煤层倾角对上覆岩层弯曲挠度的影响规律。文中得出的规律，对山区急倾斜煤层开采时顶板的控制和管理，有一定的参考价值。

［1］杨帆，麻凤海.急倾斜煤层采动覆岩移动模式及其应用［M］.北京:科学出版社，2007.

［2］胡友健，吴北平，戴华阳，等.山区地下开采影响下地表移动规律［J］.焦作工学院学报，1999，18(4):242－247.

［3］于福元，王文.采矿通论［M］.北京:中国华侨出版社，1996.

［4］黄贺.弹性薄板理论［M］.长沙:国防科技大学出版社，1992.

［5］苏仲杰.采动覆岩离层变形机理研究［D］.辽宁工程技术大学博士学位论文，2001

［6］尹志光，王登科，张卫中.(急)倾斜煤层深部开采覆岩变形力学模型及应用［J］.重庆大学学报，2006，29(2): 79－82.

［7］单祖辉.材料力学教程［M］.北京:高等教育出版社，2004.

［8］徐芝纶.弹性力学简明教程［M］.北京:高等教育出版社，2002.

Abstract:In order to research the deformation mechanism of overlying strata caused by steeply-inclined seam mining in mountainous area，a mechanical model was established.Based on the thin plate bending theory in the elastic mechanic，the prediction formula was derived.And the bending deformation of overlying strata was calculated by this formula.Result shows that the curve of bending deflection of rock plate was no longer symmetrical and the maximum value of bending deflection of overlying strata was in favor of the downhill direction of declining of rock plate because of the effect of linearly load of coal seam overlying strata caused by steeply-inclined seam mining in mountainous area; it increased with the rise of the mining depth，and the location of the maximum value of it moved gradually from the downhill direction to the midpoint of mined-out space，but the location did not overcome the midpoint and reached the raising direction of inclining rock beam;it increased with the rise of the mutation angle and the distance between the location of the maximum value and the midpoint of mind-out space becomed further and further;it reduced with the rise of the coal bed pitch，and the distance between the location of the maxim value of rock plate bending deflection and the midpoint of mind out space becomed further and further.

Key words:mountainous area;steeply-inclined coal seam;thin plate bending theory;bending deflection;overlying strata

Prediction on bending deflection of overlying strata caused by steeply-inclined coal seam mining in mountainous area

LI Hui1，LIANG Bing1，LI Gang2，BAI Yun-peng1，ZHANG Chun-mei1
(1.School of Mechanics and Engineering，Liaoning Technical University，Fuxin123000，China; 2.College of Safety Science and Engineering，Liaoning Technical University，Fuxin123000，China)

1003-8035(2010)03-0101-04

TD325

A

2010-03-17;

2010-04-06

国家自然科学基金资助项目(50874102);国家自然科学基金资助项目(50974070);国家自然科学基金(50804020);辽宁省博士启动基金(20081103)

李辉(1985—)，男，硕士，主要从事岩石力学和矿山灾害防治方面的研究。

E-mail:lh13464857601@126.com