伴随矩阵浅析
柳州城市职业学院 姜思佳 韦浩波
伴随矩阵浅析
柳州城市职业学院 姜思佳 韦浩波
本文主要通过对高职教学中伴随矩阵课程的定义做了补充:阶数为时;总结伴随矩阵的求法;并针对三角矩阵、正定矩阵、对称矩阵(包括正交矩阵)、单位阵等特殊矩阵求伴随矩阵进行了归纳总结。
伴随矩阵代数余子式初等变换
高职数学的教学中,伴随矩阵的定义注明只有n≥2阶矩阵才有伴随矩阵,文中讨论了n=1时伴随矩阵的定义。文中对求伴随矩阵的方法进行了总结,提出一种简单求法,并对特殊矩阵的伴随矩阵进行了归纳总结。
一、伴随矩阵的定义
一般教科书上伴随矩阵的定义如下

且注明只有n≥2阶矩阵才有伴随矩阵的概念,那么当n=1时,是否存在伴随矩阵呢?或者有什么样的伴随矩阵呢?我们提出如下伴随矩阵的概念:

证明 一阶方阵A的伴随矩阵定义为I1。(此处I1为一阶单位矩阵)理由如下:
设A=(k) k≠0
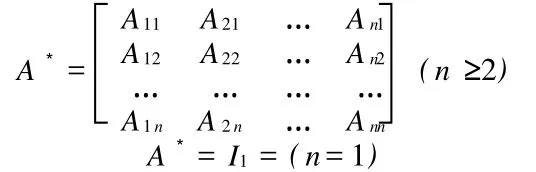
此处Aij为行列式|A|的元素aij的代数余子式(i= 1,2,3,…,n;j=1,2,3,…,n).现在我们来证明假设是否正确,即我们来证明
“n阶方阵A可逆的充分必要条件为其伴随矩阵A3可逆”是否成立?
(必要性)
1.7 菌种保存 从培养基中刮取少量新鲜菌丝转接到MEA斜面上,室温培养至菌丝覆盖整个斜面后,放入4℃冰箱保存,所有操作均在无菌环境中进行。该方法在保存过程中易出现培养基水分丧失、菌体失活,因此每隔半年须重新转接,只适合短期保存。
A可逆]A-1=存在,且|A|≠0由公式

|A3|=||A|·A-1|=|A|n-1≠0 故A3可逆。
(充分性)不妨用反证法。
若A3可逆,而A不可逆,则|A|=0,于是A·A3=|A|·I=0(零矩阵)

则与A3可逆矛盾,故A可逆。
进而对一阶方阵A:若A=(k) k≠0则相应的A3=I,而A不可逆。显然A3可逆,与上述问题二不一致。为解决上述矛盾,本文提出如下结论:
方阵的伴随矩阵定义为:A=(aij)n×n,n为正整数。

至此均得到合理的解释。 证毕
二、伴随矩阵求法
对于伴随矩阵,代数教材中介绍的普遍的算法是利用代数余子式(即伴随矩阵的元素)。对于n×n矩阵A,求其伴随矩阵A3,实际上归结为计算n2各n-1级行列式,随着矩阵阶数的增大,其计算量会迅速增大,利用矩阵的初等变换,求伴随矩阵则很容易,计算量相对很小。由矩阵的初等变换理论知,若n阶方阵A可逆,则可通过对其进行初等变换求A-1,即(A|I)~初等变换(I|A-1),具有此下面定理。
一些特殊矩阵的伴随矩阵的求法
1.三角矩阵的伴随矩阵的求法
设矩阵
2.对称矩阵求伴随矩阵
设对称矩阵为
3.单位矩阵求伴随矩阵。单位矩阵的性质和矩阵的构造我们可以容易的看出其伴随矩阵也为单位矩阵。
三、结束语
本文主要讨论伴随矩阵,对伴随矩阵的定义做了补充;总结了求伴随矩阵的一种简单方法;再就是针对一些特殊矩阵:三角矩阵、对称矩阵、单位阵等,根据它们的特殊构造对求伴随矩阵进行了归纳总结。对在高职学生掌握高等数学矩阵知识,使学生能深刻理解伴随矩阵的概念,对伴随矩阵的解法和用途细致了解,对进一步学习矩阵,以及在理论及实际应用上有十分重要意义。
[1]孟道骥.高等代数与解析几何第二版[M].北京:科学出版社,2007
[2]王航平.伴随矩阵的若干性质[J].中国计量学院学报,2004,15(3):0246~0249
[3]张禾瑞.高等代数第五版[M].北京:人民教育出版设,2007
[4]北大数学系代数与几何教研室前代数小组编.高等代数第三版[M].北京:高等教育出版社,2003
book=80,ebook=163

