带参数扰动的永磁同步电动机混沌系统的鲁棒自适应主动控制

李钟慎,傅桂元

(华侨大学机电及自动化学院,福建泉州362021)

带参数扰动的永磁同步电动机混沌系统的鲁棒自适应主动控制

李钟慎,傅桂元

(华侨大学机电及自动化学院,福建泉州362021)

基于自适应主动控制,提出一种鲁棒控制方法,通过估计不确定性系统参数的上、下界限,设计自适应主动控制器.同时,给出具体的理论推导及稳定性分析.该方法可以有效消除系统参数扰动的影响,从而实现使永磁同步电机各状态变量能被镇定到任意点,以及输出能渐近跟踪任意期望轨道.数值仿真结果验证了方法的有效性及鲁棒性.

永磁同步电动机;自适应主动控制;参数扰动;混沌控制;鲁棒性

永磁同步电动机(PM SM)在一定条件下将呈现出混沌特性,主要表现为转矩和转速的间歇振荡、控制性能的不稳定、系统不规则的电流噪声等[1-2].这对于永磁同步电动机稳定运行极为不利,甚至将引入整个驱动系统的损坏.因此,永磁同步电动机的混沌控制研究具有很大的实际意义.目前,实现对永磁同步电动机的混沌控制的方法,主要有自适应反步法[3]、主动反步法[4]、无源控制方法[5]、自适应动态面方法[6]、Lyapunov指数方法[7]、基于模糊控制的自适应滑模控制[8]、有限时间理论[9]和LaSalle不变集原理[10]等.但是,上述各方法中均没有考虑系统受到参数扰动或是外部不确定性因素的情况.在实际应用中,应避免受到各种干扰等不确定性因素的影响,因此,研究具有参数扰动不确定性的永磁同步电动机的混沌控制问题具有较大的实际应用价值.文[11]提出一种基于线性反馈方法实现对永磁同步电动机的镇定及跟踪控制,并且分析了系统存在模型误差及测量噪声情况下的鲁棒性.但该方法将永磁同步电动机混沌模型中的两个状态量(分别d,q轴电流)用自定义的两个状态变量来表示,显然在实际应用当中要受到很大的限制.本文设计基于自适应主动控制的自适应鲁棒控制器,实现对具有参数扰动的不确定性PM SM混沌系统的鲁棒控制.

1 永磁同步电动机的混沌模型

由文[1-2]可知,永磁同步电动机混沌系统的数学模型为

式(1)中:状态变量ω,i,i分别表示电动机的转子角速度、定子d,q的轴电流;～T,～u,～u分别为负载转

dqLqd矩、定子d,q的轴电压.这里,只考虑系统没有受到驱动负载的情况,即～u=～u=～T=0.此时,系统(1)

可以写成如下形式,即

由文[2]可知,当参数σ=5.46,γ=20时,系统(2)将呈现出混沌特性.然而,实际模型中的系统(2)的参数σ,γ将会受到各种环境因素的影响,因而含有各种不确定性.考虑被控系统(2)带有参数扰动情况时,其表述为

式(3)中:Δσ,Δγ分别表示系统参数的扰动项;变量y为系统(3)的输出量;u=[u1,u2,u3]T为系统的控制输入.控制目标首先是使带有参数扰动的被控系统(3)的各状态变量稳定到任一点,其次是使系统的输出能快速跟踪到期望轨道.

2 控制器的设计

2.1 镇定问题

假定被控永磁同步电动机的各状态变量的期望值为[ωr,iq,r,id,r],则系统的各状态误差分别为e1= ω-ωr,e2=iq,iq,r,e3=id,id,r.不失一般性,为了便于分析,取系统的状态原点作为各状态变量的期望值,即[ωr,iq,r,id,r]=[0,0,0].则系统动态误差方程为

系统的控制目标是使式(4)中的各状态变量满足

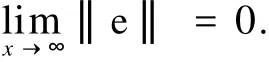
考虑带有扰动项的系统参数为时变,即σ(t)=σ+Δσ,γ(t)=γ+Δγ.假定σ(t)∈[σ,σ¯],γ(t)∈[γ, ¯γ].将被控系统(4)写成矩阵形式,则有

式(5)中:矩阵A为系统确定性参数;ΔA为系统参数扰动量;f(x)为系统的非线性向量函数,u为系统的控制向量组,其值分别如下

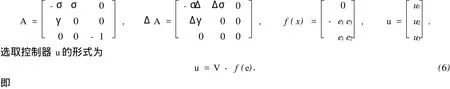
此时,系统(4)可以看成是一时变的线性系统.不失一般性地,可以假定V=Pe,其中P是一个3×3的矩阵.则式(7)可改为渐近趋于零.

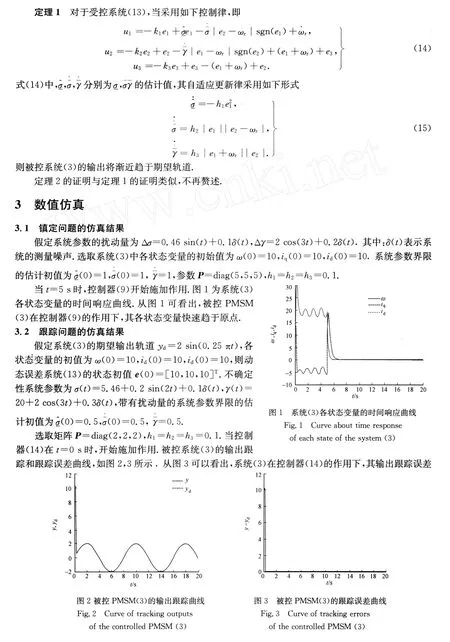
4 结束语

提出一种鲁棒控制方法,实现对具有参数扰动的不确定性PM SM混沌系统的镇定及跟踪.采用自适应主动控制,通过估计不确定性参数的上、下限,设计鲁棒控制器,有效消除了被控系统中参数扰动的影响,并给出了具体的设计步骤及理论推导.该方法适应性广,设计的控制器简单易行.

[1] L IZhong,PARK J B,ZHANGBo,et al.Bifurcations and chaos in a permanentmagnet synchronousmo to r[J].IEEE Trans Circ Sys(Ⅰ),2002,49(3):383-387.

[2] 张波,李忠,毛宗源.永磁同步电动机的混沌模型及其模糊建模[J].控制理论与应用,2002,19(6):841-844.

[3] GE Xiao-hui,HUANGJin.Chaos controlof permanentmagnet synchronousmotor[C]∥Proc of the 8th International Conf Electrical Machines and Systems.Nanjing:[s.n.],2005:484-488.

[4] 李钟慎,魏剑林,王永初.利用Backstepping方法的PMSM混沌运动的控制[J].华侨大学学报:自然科学版,2009, 30(3):253-256.

[5] Q IDong-lian,WANGJia-jun,ZHAO Guang-zhou.Passive control of permanent magnet synchronousmotor chaotic systems[J].J Zhejiang Univ Sci(A),2005,6(7):728-732.

[6] W EID Q,LUO X S,WANGB H,et al.Robust adap tive dynamic surface controlof chaos in permanentmagnet synchronousmoto r[J].Phys Lett(A),2007,363(1/2):71-77.

[7] ZRIB IM,OTEAFY A,SMAOU IN.Controlling chaos in the permanent magnet synchronous moto r[J].Chaos, Solitons and Fractals,2009,41(3):1266-1276.

[8] POURSAMAD A,MARKAZIA H D.Adap tive fuzzy sliding-mode control formulti-inputmulti-output chaotic system s[J].Chaos,Solitons and Fractals,2009,42(5):3100-3109.

[9] WEIDu-qu,ZHANGBo.Controlling chaos in permanent magnet synchronous moto r based on finite-time stability theo ry[J].Chinese Physics(B),2009,18(4):1399-1403.

[10] 韦笃取,罗晓曙,丘东元,等.基于LaSalle不变集定理自适应控制永磁同步电动机的混沌运动[J].物理学报, 2009,58(9):6026-6029.

[11] REN H,L IU D.Nonlinear feedback controlof chaos in permanentmagnet synchronousmoto r[J].IEEE Trans Circuits Syst(Ⅱ),2006,53(1):45-50.

Robust and Adaptive Active Control of the Chaotic System in Permanen t Magnet Synchronous M otor with Parameters Perturbation

L IZhong-shen,FU Gui-yuan
(College of Mechanical Engineering and Automation,Huaqiao University,Quanzhou 362021,China)

A robust controlmethod is p roposed and the bounds of the uncertain system parameters are estimated based on adap tive active control so that the adap tive active controller could be designed.Meanw hile,the detailed theo retical derivation and stability analysis is given.The controlmethod can effectively eliminate the influence of the system parameters perturbation,and each state of PMSM can be driven to any user-defined point and the outputs can asymp totically track any desired orbit.The resultsof numerical simulation have show n that the effectiveness and robustness of the p roposed control scheme.

permanentmagnet synchronousmotor;adap tive active control;parametersperturbation;chaotic control;robustness

TM 351.012;TP 273+.2;O 415.5

A

(责任编辑:陈志贤 英文审校:郑亚青)

1000-5013(2010)06-0615-05

2010-01-11

李钟慎(1971-),男,教授,主要从事最优控制、时滞系统的控制、抗饱和控制的研究.E-mail:lzscyw@hqu. edu.cn.

福建省自然科学基金计划资助项目(E0710018)