小波分析在土木工程抗震方面的应用

海军工程质量监督站 刘楚瑜

1、前言

小波变换是一种新的变换分析方法，它的主要特点是通过变换能够充分突出问题某些方面的特征。因此，小波变换在许多领域都得到了成功的应用，特别是小波变换的离散数字算法已被广泛用于许多问题的变换研究中。

从小波变换的数学理论来说，它是继Fourier变换之后纯数学和应用数学完美结合的又一光辉典范，享有“数学显微镜”的美称。从纯粹数学的角度来说，小波变换是调和分析（包括函数空间、广义函数、Fourier分析和抽象调和分析等）这一重要学科大半个世纪以来的工作结晶；从应用科学和技术科学的角度来说，小波变换又是计算机应用、信号处理、图像分析、非线性科学和工程技术近些年来在方法上的重大突破。

2、小波分析的基本理论

与傅利叶(Fourier)变换相比，小波分析中所用到的小波函数具有不唯一性，即小波函数Ψ(t)具有多样性。但小波分析在工程应用中，一个十分重要的问题就是最优小波基的选择问题，因为用不同的小波基分析同一个问题会产生不同的结果。目前主要是通过小波分析处理信号的结果与理论结果的误差来判定小波基的好坏，并由此限定小波基。但并不是随便一个函数都可以成为小波基函数，要满足非常严格的限制才能成为一个可用的小波函数，进而发展成一个好的小波变换函数。

考虑平方可积的实数函数空间L2(R)（即能量有限的信号空间），设Ψ(t)∈L2(R)，其傅利叶变换为，当满足(1)式允许条件(Admissible Condition)时，我们称为一个基本小波，或小波母函数(Mother Wavelet)。

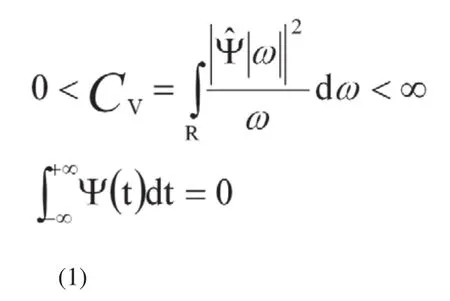
根据不同的标准，小波函数具有多样性，实际应用中应根据支撑长度、对称性、正侧性等标准选择合适的小波。常用的小波有：Haar小波、Daubechies(dbN)小波系、Biorthogonal(biorNr.Nd)小波系、Coiflet(coifN)小波系、SymletsA(symN)小波系、Morlet小波、Mexican Hat小波、Meyer小波、Battle-Lemarie小波等。

2.1 多分辨分析

1988年，Mallat在构造正交小波基时提出多分辨分析(Multi-Resolution Analysis)的概念，给出了离散正交二进小波变换的金字塔算法，即任何函数f(t)∈L2(R)都可以根据分辨率为2-N的f的低频部分（“近似部分”）和分辨率为2-j(1≤j≤N)下f的高频部分（“细节部分”）完全重构。多分辨分析只是对低频部分进一步分解，而高频部分则不予考虑。

分解具有关系：

f(t)=An+Dn+Dn-1+…+D2+D1，其中，f(t)代表信号，A代表低频近似部分(Approximations)，D代表高频细节部分(Details)，n代表分解层数。

2.2 小波包分析

多分辨分析可以对信号进行有效的时频分解，但由于其尺度是按二进制变化的，所以在高频频段其频率分辨率较差，而在低频频段其时间分辨率较差。小波包分析(Wavelet Packet Analysis)能够为信号提供一种更加精细的分析方法，它将频带进行多层次划分，对多分辨分析中没有细分的高频部分进一步分解，并能根据被分析信号的特征，自适应的选择相应的频带，使之与信号的频谱相匹配，从而提高了时频分辨率，因此，小波包分析具有更广泛的应用价值。

分解具有关系：

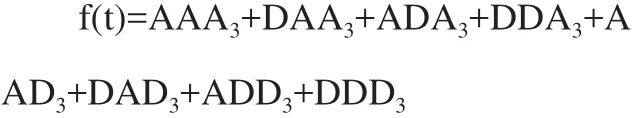
其中，f(t)代表信号，A代表低频近似部分，D代表高频细节部分，下标代表分解层数。

3、小波分析在抗震方面的应用

对地震动的了解主要是根据过去强震观测结果和震害现象去探求地面运动规律和地震动特性。描述地震动特性所用的数学工具以往是Fourier分析，其特性归结为三要素，即地震动的振幅、频谱和持时。三要素的得出是将Fourier分析应用于地震动研究的结果。Fourier分析的另一个名称是频谱分析。

对于地震动研究而言，Fourier分析有明显的不足多处，Fourier分析适合处理非常平稳的周期信号，对于具有很强非平稳特性的地震动加速度过程，Fourier分析无法得出时域和频域中地震动加速度过程的全貌和局部化结果，无法依据地震观测记录建立地震动加速度过程的解析表达式。强震观测记录分析表明，在不同时段上周期特性是不一样的，一般来说，开头部分，即是纵波部分，高频分量比较多；尾部，即振动衰减趋于零部分，低频分量比较多。振动最强烈的一段，即中间部分，中频分量比较多。目前地震工程中常用的频谱有三种，即Fourier谱，反应谱与功谱。地震记录的这种频谱组成随时间变化的特性，是前面三种频谱无法描述的。

小波分析作为处理非平稳信号的强有力工具，同样适合于用于处理地震动加速度过程，其理论覆盖了相当广泛的研究领域，它为多种独立开发的信号处理提供了统一的框架。小波分析方法不像Fourier分析方法那样把时域信号表示为若干精确的频率分量之和，小波变换提供了一种自适应的时—频局部化分析方法，它将时域信号表示为若干代表子频带特点的时域分量之和，这些时域分量正是小波变换所确定的。正是由于这种表示方式，小波分析方法才获得了在时—频局部化方面的成功和关于时—频局部化方面丰富多彩的应用。应用小波分析方法可在任意时段上对地震动加速度过程的频率成分和振幅进行调整，以反映地震动过程的频谱组成随时间的变化，对频谱和振幅进行精细描述。这为工程设计时，输入地震波的选择扩大了范围。我们可以制造一批频谱组成随时间变化不同，但反应谱相同的地震动样本，以满足建筑结构统计分析的需要，同时这对结构非线性地震反应分析和实验研究也是极为有用的。用小波分析方法可以直观具体地检测现有强震加速度记录中长周期成分的缺失状况，并以某种方式进行添补。

目前，模拟强地震动的方法以工程方法为主，现有工程方法合成地震动的最大缺陷是频率从头至尾不变。将小波分析方法用于强地震动模拟，能够克服现有工程方法的上述缺陷，并且为强地震动模拟提供一个灵活的“框架”。

TsoChienPan等将双线性结构在地震作用下的响应分别用窗口傅立叶变换(STFI)、连续小波变换(CWT)、和离散小波变换(DWT)进行分析，其目的是识别双线性结构地震响应的频率变化趋势和屈服、卸载时间。结果表明，CWT在时间和频率的分辨率上均优于STFT；CWT能反映出双线性结构振动频率变化的趋势，但DWT从低尺度上的小波系数出现突变点更好地反映出结构的屈服时间和卸载时间，Yoshihiro将系统(线性结构、双线性结构、Ramberg-Osgood系统)的切线刚度用尺度函数表示，通过测出系统在地震作用下的响应，用最小二乘法求出Pjk，从而得到S(t)来识别系统的非线性行为。JunIyama等基于能量输入的观点用小波变换对地震在不同频带的信号的时间历程进行了分析，提出了一种根据预想时一频特点模拟地面运动加速度的方法。

4、结论与展望

总之，小波变换被应用到抗震方面的研究尚较少。从研究方向来看，大多数都集中在某类简单结构上，不具有推广性；从研究理论上来看，很多文献都偏重于介绍故障信号的小波变换结果，而缺乏理论上的有力支持，真正实现小波分析与故障信号间关系的文献极少。小波变换作为一种新兴的时频分析手段，在处理结构测试数据时具有极大的优势，可以预见其在土木工程领域中特别是抗震方面有着广阔的发展空间和应用价值。