基于控制拉格朗日函数法的车载倒立摆的稳定性
杨 峻, 王 红
(1.安阳师范学院数学与统计学院 河南安阳455002;2.南开大学数学科学学院 天津300071)
基于控制拉格朗日函数法的车载倒立摆的稳定性
杨 峻1, 王 红2
(1.安阳师范学院数学与统计学院 河南安阳455002;2.南开大学数学科学学院 天津300071)
在自由系统拉格朗日函数基础上,通过更改其中动能函数的度量张量,构造了控制拉格朗日函数.说明了控制拉格朗日函数法在系统稳定性研究中的使用方法和步骤,并运用此方法研究了车载倒立摆的稳定性,得出了相关结论.
倒立摆;控制拉格朗日函数;动能;稳定性
0 引言
倒立摆是动力学和控制理论中的一个经典问题,被普遍认为是检验控制算法(如PID控制器、神经网络、模糊控制、遗传算法等)的基准.倒立摆的稳定性问题被广泛应用于航空航天、机械制造等相关领域[1].控制拉格朗日函数法是研究欧拉-拉格朗日运动方程所能描述的众多物理系统稳定性的有效方法.这种方法的指导原则是寻求一种闭环系统的控制律,然后用线性化等方法确定平衡的稳定性[2].
本文首先介绍控制拉格朗日函数法,然后运用这个方法来研究车载倒立摆的稳定性.
1 控制拉格朗日函数法
控制拉格朗日函数法是在力学系统的自由拉格朗日函数(即系统的动能减去势能)[3-5]基础上,靠修改系统动能来构造一个新的函数,它能够描述闭环系统动力学,称为控制拉格朗日函数.
假设系统所在的位形空间为Q,且具有形式Q=S×G,其中G是一个李群,用直接控制G中变量的方法来控制S中的变量.假定G在Q上有变化时,拉氏函数保持不变,这里的变化只在G上发生.在下面给出的例子中,拉氏函数的不变特性等同于它在G变量中是循环的.因此,得出了自由系统的守恒定律.在我们的构造方法中,仍要保持拉氏函数不变的特性,故而会带来一个改进的守恒定律.
Q的切空间[6]可被分成水平和垂直两大部分.对于Q上一点q处Q的每一切向量vq,可写出唯一分解式vq=Ho rvq+Vervq,使得垂直部分是G的切向量,水平部分则由式(1)唯一定义,

其中,vq和wq是任意切向量.这种对向量的分解可直观地看作是分成了两块,一块是按对称性或群方向上的(垂直部分),另一块是按外形或内部方向上的(水平部分).例如,在一个振动分子中,这种分解相当于分子的自旋和振动模式.
对式(1)作一个修改,势能保持不变,修改包含3方面内容:1)选取一个不同的水平空间,记作Horτ;2)一个作用在水平向量上的度量变换g→gσ;3)一个作用在垂直向量上的度量变换g→gρ.控制拉氏函数等于修改后的动能减去势能,Lτ,σ,ρ=[gσ(Ho rτvq,Ho rτwq)+gρ(Verτvq,Verτwq)]-V(q),其中,V是势能.与这个拉氏函数对应的方程是闭环系统方程,这些方程中出现的与控制变量对应的新条件将作为控制输入.
以ξQ表示对应于李代数元素ξ的极小生成元,新的水平空间由形如Horτvq-[τ(v)]Q(q)的向量组成,其中τ是消去了垂直向量的1形式[6].
在车载倒立摆的实例中,可以取gρ=g(即ρ不必要出现),引入一个标量σ,只用gσ去修改群方向上的原始度量g,这样,控制拉氏函数具有形式
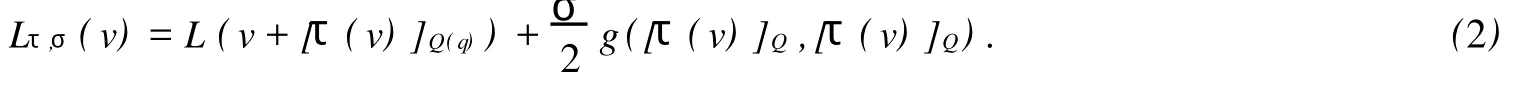
概括起来,一般的做法是:
a)从一个具有拉氏函数和对称群G的力学系统开始,其中拉氏函数具有动能减势能的形式(在下面的车摆系统的例子中,对称群指的是水平方向).
b)写出自由系统的运动方程.
c)引入τ,σ,ρ,给出控制拉氏函数.
d)写出与控制拉氏函数相应的运动方程,在方程的对称变量中迅速得到控制律u.
e)选取τ,σ,ρ,使得受控的原始系统的欧拉-拉格朗日方程(即带控制输入的含有拉氏函数L的欧拉-拉格朗日方程)与针对控制拉氏函数Lτ,σ,ρ的欧拉-拉格朗日方程相匹配.用欧拉-拉格朗日方程消去加速度来确定反馈控制律u,这样,反馈控制律有可能只依赖于速度.
f)自由选取τ,σ,ρ,用线性化方法或能量-动力法来确定平衡的稳定性.
2 车载倒立摆的稳定性
现将上述思想应用于车载倒立摆系统,并讨论该系统的稳定性.首先给出车摆系统的拉氏函数,设s表示S轴上小车的位置,θ表示摆与垂直方向的夹角,l为摆长,M,m分别是小车和摆锤的质量,g为重力加速度,如图1所示.这里,位形空间Q=G×S=R×S1,R表示车的坐标s,S1表示摆角θ.速度的相空间TQ坐标为(s,θ,˙s,˙θ).

图1 车载倒立摆系统的运动Fig.1 Motion of inverted pendulum on a cart
相对于实验标架的车速是˙s,相对于实验标架的摆速是向量
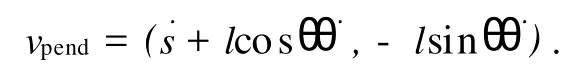
系统的动能恰为车和摆动能的总和,

拉氏函数是动能减去势能,于是有

其中,势能V=m g l cosθ.为方便起见,将拉氏函数改写为

其中,α=m l2,β=m l,γ=M+m,D=-m g l均为常数,注意有αγ-β2>0.
关于s和θ的动量分别是ps=γ˙s+βcosθ˙θ与pθ=α˙θ+βcosθ˙s.
相对平衡状态定义为θ=0,˙θ=0,˙s=0.由于D<0,故是不稳定的.
逐步形成以凤山古镇、白云古洞、云雾山、窟窿山等自然景观与郭小川故居、丰宁剪纸,丰宁布糊画等人文景观相结合的乡村旅游发展节点,重点发展乡村旅游体验、休闲农业旅游产品,规划项目形态为旅游民俗村与休闲农庄等基础配套设施,重点挖掘乡村文化,形成文化底蕴,使丰宁东北乡村旅游稳步发展。
由于s是一个循环变量,故包含作用于小车的控制力u(没有直接的力作用到摆上)的车摆系统的运动方程为

下面根据前述方法,通过修改自由车摆系统拉氏函数的动能,来构造控制拉氏函数.
最一般的s不变水平1形式为τ=κ(θ)dθ,σ是一个标量,利用式(2),有
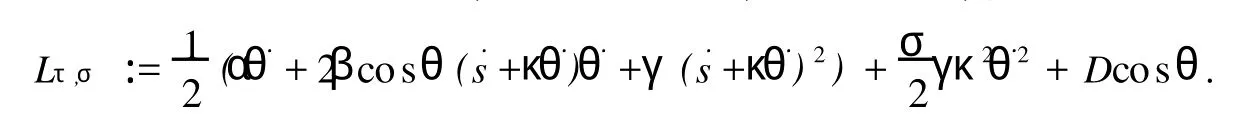
因为变量s仍是循环的,按照前述步骤,靠观察守恒律的变化来寻找反馈控制量.联系新的拉氏函数Lτ,σ,有守恒律

对于动量ps,有

这样,当控制力加于小车时,确定出了(5)式的条件.
仍利用控制拉氏函数,象(4)式一样,计算得到θ的方程为

下一步要选取κ和σ,使包含控制拉氏函数的方程(6)能匹配被控小车的θ方程(3).根据(5)式给出的控制律,被控小车的θ方程为
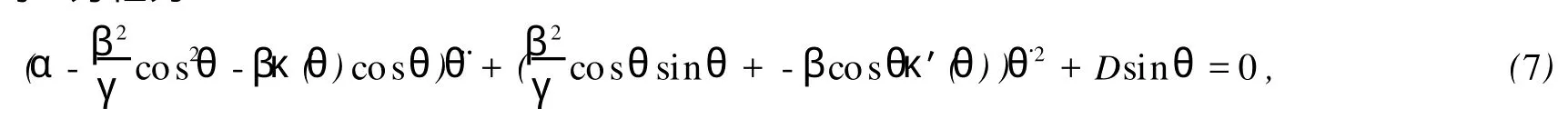
比较方程(6)和(7),有σγ[κ(θ)]2=-βκ(θ)cosθ.由于σ为常量,令κ(θ)=κcosθ,其中,κ是一常数(故σ= -β/γκ).
接下来代换(5)式中θ¨及κ(θ),得到非线性控制律

考察闭环系统的线性化情形,会发现当

对于车摆系统(3),当κ满足(9)式时,便得出系统稳定化的反馈控制律(8).
简单的计算表明,ζ的分母不为零,因为θ满足sin2θ 这种方法的优点是:首先,系统的稳定性完全可以在力学的背景下完成,可以用能量的观点来理解;其次,尽管稳定性是依靠控制外力实现的,但仍保留有系统机械能的一种延伸,可以把它理解为关于力学系统和控制外力的一种联合能量. [1] 郭晓丽,方建印.Lyapunov稳定性逆定理的另一种证明[J].郑州大学学报:理学版,2004,36(2):22-24. [2] 宋军烈,肖军,徐心和.倒立摆系统的Lagrange方程建模与模糊控制[J].东北大学学报:自然科学版,2002,23(4): 333-336. [3] 高为炳.运动稳定性基础[M].北京:高等教育出版社,1987. [4] 秦元勋,王联,王慕秋.运动稳定性理论与应用[M].北京:科学出版社,1981. [5] 沈惠川,李书民.经典力学[M].合肥:中国科学技术大学出版社,2006. [6] 陈省身,陈维桓.微分几何讲义[M].北京:北京大学出版社,2001. Stabilization of the Inverted Pendulum on a Cart by the Method of Controlled Lagrangian YANG Jun1, WANG Hong2 A controlled Lagrangian by modifying the metric tensor of Lagrangian for the uncontrolled system is constructed.The methods and step s of using controlled Lagrangian fo r the research of system stabilization are introduced.Then the stabilization of the inverted pendulum on a cart is studied by this app roach.And relevant conclusions are draw n. inverted pendulum;controlled Lagrangian;kinetic energy;stabilization O 302 A 1671-6841(2010)03-0051-03 2009-12-31 国家自然科学基金资助项目,编号10171081;2005年天津市自然科学基金资助项目. 杨峻(1973-),男,讲师,硕士,主要从事应用数学研究,E-mail:yumoym@163.com.
(1.School of M athem atics and Statistics,Anyang Norm al University,A nyang 455002,China; 2.School of M athem atical Sciences,N ankai University,Tianjin 300071,China)
——《势能》

