一类极大平面图4-着色布尔方程组
贾永旺, 白莲花, 乌力吉
(内蒙古工业大学理学院 内蒙古呼和浩特010051)
一类极大平面图4-着色布尔方程组
贾永旺, 白莲花, 乌力吉
(内蒙古工业大学理学院 内蒙古呼和浩特010051)
对极大平面图的4-着色布尔方程组进行研究,得到了该布尔方程组的5条性质,并且给出了求极大平面图4-着色全部解的一个算法.
平面图;极大平面图;4-着色;布尔方程组
0 引言
图的着色问题具有重要意义,是图论的主要研究内容之一.图的着色问题的研究起源于著名的4色猜想,即,每张地图是否可以用4种颜色对国家进行着色,使得相邻的国家着不同的颜色.1977年文献[1]通过计算机得到4色猜想证明,然而这一证明并没有给出具体4-着色方法.目前,介绍求极大平面图4-着色全部解的报道还很少见,对于给定平面图应该怎样去着色,仍然没有一种行之有效的办法.文献[2-4]将极大平面图的4色问题转化为简单布尔方程组的求解问题,为研究4色问题开辟了一条新的途径,文献[5-9]对此问题也作了研究.
我们对这类方程组进行了探讨,得到了它的5条重要性质,为求解该类问题打下了理论基础.最后给出了求极大平面图4-着色解的一个算法,该算法与以往的带有穷举性质的算法不同,它不需要试探步,得到的都是正常4-着色解,从而提高了效率,同时它求出来的还是全部解.在本文中,凡不加以说明的名词术语和符号,均采用文献[3]中的规定.
1 基本概念
定义1[2]在一个圈中添加一个新的顶点,并将新顶点与圈上所有顶点以边连接后所得的图称为轮图.新边称为轮图的辐,记为Wn.
在Wn中可对应n个不同的同构于K4-e的子图,在每个子图上定义一个布尔变量xi(1≤i≤n),用其表示K4-e中对应的二度顶点着色时颜色的异同(1表异色,0表同色,下同).设G是极大平面图,设∏1,∏2,…,∏n是G的同构于K4-e的子图全体集,对每个∏i,如前定义一个变量xi,G的正常4-着色全体集C与n维布尔向量空间Vn的一个子集一一对应,在n维布尔向量空间或1,i=1,2,…,n}上定义了一个布尔函数

我们已有求Fn(x1,x2,…,xn)的递推公式,其中,表示xi的逆元(下同):
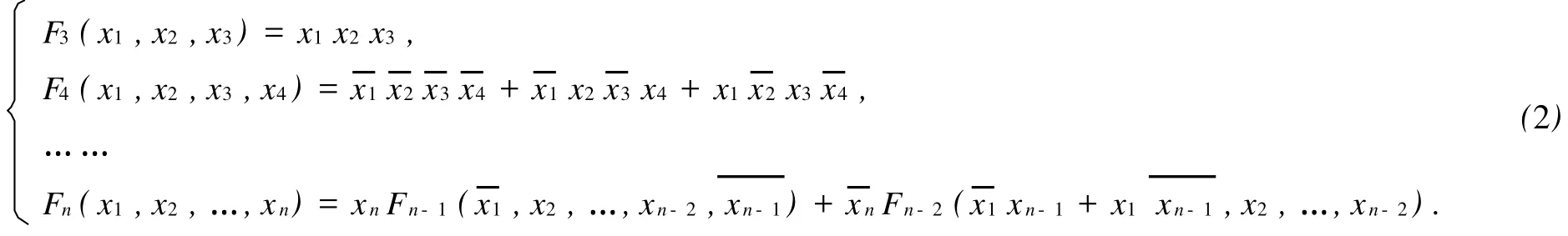
设G的内部顶点全体之集为{v1,v2,…,vk},对每个vi(i=1,2,…,k),得到一个轮图Wi=G[vi∪N(vi)],这里N(vi)={u|viu∈E(G)}.由Wi又可以定义一个布尔函数Fi,这样,就得到了布尔方程组我们称其为G的4-着色布尔方程组,其中,上标表示方程的编号,下标表示方程中含有变量的个数.

引理1[2]任一极大平面图G可4-着色问题当且仅当布尔方程组(3)有解,进一步地,(3)的每个解向量都对应着G的一个正常4-着色,反之亦然.
2 主要结果
设G是极大平面图,其顶点集为{v1,v2,…,vn},对其4-着色布尔方程组进行了研究,得到了它的5条性质,并且给出了极大平面图4-着色全部解的算法.
定义2把有n个布尔变量x1,x2,…,xn排成的序列看成是首尾相连的环状序列,则由其中xk(1≤k≤n)处断开,得到新的序列xk+1,xk+2,…,x1,x2,…,xk的过程,称为序列关于xk的一个轮换,新序列记为xk+1,…,xn,…,xk.本文中,当不会发生混淆时,将采用该记号.
2.1 布尔方程组的性质
定理1对序列x1,x2,…,xn进行一个轮换后,布尔函数(1)的值不变,即

证明采用数学归纳法证明.
当n=3时,显然有F3(x1,x2,x3)=F3(x2,x3,x1)=F3(x3,x1,x2)=x1x2x3;
当n=4时也可以类似验证命题成立.假设n 下证当n=m时命题成立. 再由(2)式可知,一方面等式的左端 另一方面,求证等式右端 上面公式左右两端都等于4项的和,根据归纳假设可知,这4项分别对应相等.所以当n=m时,命题也成立.综上,命题成立. 定理2公式中函数具有性质 证明 定理3布尔函数(1)都可递归展开成一个析取主范式. 证明采用数学归纳法证明. 当n=3,4时展开式中的每一项恰好是布尔函数(1)的一个极小项,结论显然成立. 假设命题在n 推论1对序列x1,x2,…,xn进行一个轮换后,布尔函数(1)的主范式不变. 定理4在布尔方程组(3)中,每个变量xi(1≤i≤n)至多在两个方程中出现;另外,如果某两个方程中含有公共变量个数多于一个,则这几个变量相等. 证明从略(根据布尔变量的引入方式易得). 定理5如果在(3)中第i个和第j个方程含有一个公共变量xk,那么…,xn)=1的充分必要条件是.其中, 如果在上述表达式中,xk+1,xk+2,…,xn,x1,x2,…,xk-1某一变量没有出现,则其他变量依次递进. 2.2.1 算法思想 2.2.2 算法步骤 步骤1)读入表示极大平面图的布尔方程组(3); 步骤2)判断所有变量是否都已经包含在唯一方程中,若是则转步骤4,否则转步骤3; 步骤3)选定变量xk,取出包含xk的两个方程,利用定理5将其合并为一个方程,并用新方程代替原方程组中的这两个方程,转步骤2; 步骤4)根据定理3将每个方程左端的布尔函数递归展开为一个析取主范式,得到每一个布尔函数的成真赋值. 2.2.3 收敛性分析 根据算法原理可知,程序每运算一次可以消去一个方程,而每个变量至多包含在两个方程中,所以如果(3)中含有n个变量,则至多运算n次后,可将所有的变量化为只包含在唯一方程的情形,然后将每个方程递归展开就得到了(3)的全部解,所以,该算法是在有限步骤内收敛的. [1] Appel K,Hakn W.Every planar map is four colo rable[J].Illinois JMath.1977,21(3):429-490. [2] 乌力吉.平面图的4-着色的简单布尔方程表示[J].内蒙古大学学报:自然科学版.2001,32(1):1-5. [3] 邦迪JA,默蒂USR.图论及其应用[M].吴望名,译.北京:科学出版社,1984. [4] 乌力吉.平面图正常4-着色数的一个计算公式[J].内蒙古大学学报:自然科学版.2001,32(2):119-124. [5] 贺佩玲,黄元秋.W_4×S_n的交叉数[J].郑州大学学报:理学版,2009,41(1):6-9. [6] 刘广军,刘信生.P_m∨W_n的点可区别全色数[J].郑州大学学报:理学版,2007,39(4):14-21. [7] 杨爱峰,原晋江.图的相邻强边着色数[J].郑州大学学报:理学版,2004,36(2):7-9. [8] 董海燕,孙磊,孙艳丽.关于邻点可区别全染色的几个新结果[J].广西师范大学学报:自然科学版,2005,23(3):41-43. [9] 唐高华,高艳艳,林光科.几类简单图的交换零因子半群[J].广西师范大学学报:自然科学版,2009,27(1):25-28. The Maximum Planar Graph 4-Colorings Boolean Equation Group JIA Yong-w ang, BA ILian-hua, U lji The maximum p lanar graph 4-colorings Boolean equation group is studied,and some useful p roperties is obtained.A p roper 4-coloring algorithm is p rovided for maximal p lanar graphs.The algorithm can find all p roper 4-coloring solutions for any given maximal p lanar graph. p lanar ganphs;maximal p lanar graph;4-colo ring;Boo lean equation group O 157.5 A 1671-6841(2010)03-0037-04 2010-02-28 内蒙古自然科学基金资助项目,编号200607010115. 贾永旺(1975-),男,讲师,硕士,主要从事图论与组合优化研究,E-mail:jyw_zhy@sina.com.







2.2 极大平面图4-着色全部解算法
(College of Science,Inner M ongolia University of Technology,Hohhot 010051,China)

