基于损伤的渗流-应力耦合模型在工程地下水迁移研究中的应用
张 莱,陆桂华
(1.河海大学水文水资源学院,江苏南京 210098;2.中国煤炭地质总局水文地质工程地质环境地质勘查院,河北邯郸 056004;3.江苏省水利厅,江苏南京 210029)
岩石损伤是工程岩体在水的渗流与应力相互作用下的变形和破坏,是许多工程共同关心的问题。在岩土边坡、矿井突水、油汽开发、水电站大坝运行、核废料地下处理的污染泄漏等工程中,地下岩石与地下溶洞受高应力、高水压的作用,尤其是裂隙,在高压、高水头和复杂的化学侵蚀作用下,裂隙的发育发展影响到整个工程的安全。当前国内外有许多学者致力于渗流-应力耦合问题的研究[1-3],并且提出了多种理论分析和数值模拟模型[4-7]。多数学者的研究偏向于流场(流体力学)作用于固体(岩体)产生反应(包括岩体的变形、破坏、稳定性等)[8-10],只有少数学者研究固体骨架(岩体)的纯力学作用。
为探求一种清晰明了的耦合关系模型,本文基于岩石受载过程强度弱化源于内部缺陷生长的概念,推导了基于应变(变形)的损伤演化方程,描述了岩石强度变化的非线性特征,并采用应变-损伤-渗透性关系方程描述耦合关系,开发了工程计算效果较好的渗流-应力耦合的非线性计算程序。
1 岩石损伤本构关系及损伤演化方程
1.1 三维损伤变量及演化方程
引入Lemaitre损伤变量εc描述三维损伤并构建演化方程:
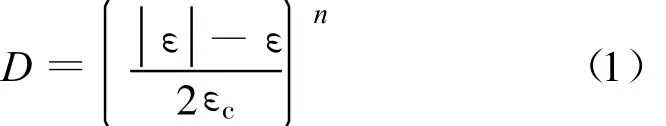
式中:D为三维损伤变量;ε为轴向应变;εc为常量;n为材料脆性参数,与材料脆性有关。
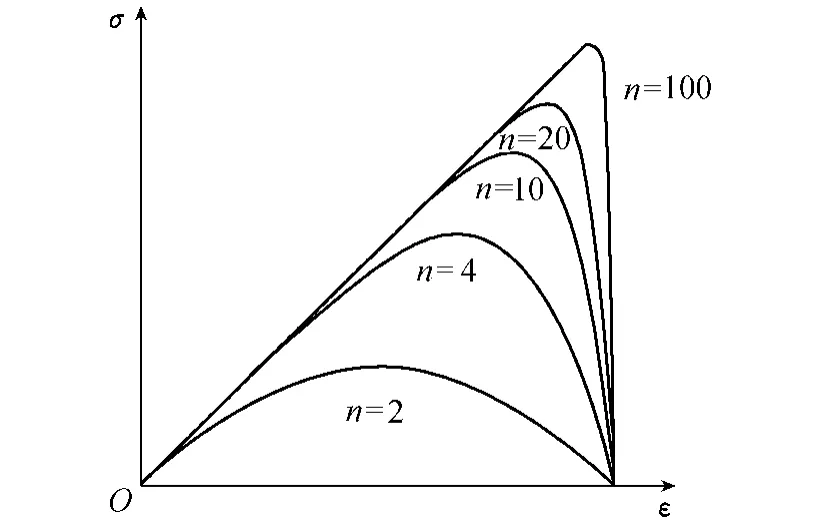
图1 损伤材料应力应变关系
如图1[11]所示,εc是当n→∞时的弹性应变上界值,包括破坏前应变和破坏后的残余应变。即损伤的演化取决于应变状态的变化,应变状态的变化又与损伤状态有关。一维状态的损伤演化方程可以在主应力空间扩展到三维。对脆性岩石材料而言,在裂纹尖端的局部区域内可能不会出现塑性屈服,而是脆性破坏后的微小碎末区域包含在未破坏的完整岩石之中。因此,在描述损伤演化的时候就不能认为岩石破坏后仍然具有承载能力,残余应变也就无从谈起。εc为包含残余应变的容许值,应当去除残余应变,其值等于峰值应力对应的应变。采用最大拉应变准则来判定材料是否破坏是合适的。临界状态为

试验表明混凝土材料在单轴压缩时的损伤是张应力引起的,损伤方向与载荷方向正交。这表明混凝土的损伤是各向异性或正交各向异性的[12]。坚硬岩石材料与混凝土材料性质相似,可认为岩石材料的损伤是正交各向异性的。在主应力空间,应力主轴、应变主轴和损伤主轴互相重合。材料初始状态是各向同性的线弹性体,损伤后表现出正交各向异性性质。在此假定下,损伤张量D和应力张量σ均为二阶张量,设3个主损伤分量为D1,D2,D3,则根据热力学第二定律、一维损伤的定义式及损伤变量的物理意义,并令

式中:ν为泊松比。
在单轴压缩状态(σ1>0,σ2=σ3=0),有 ε1>0,ε2=ε3=ε′,ε′<0,则式(3)变为
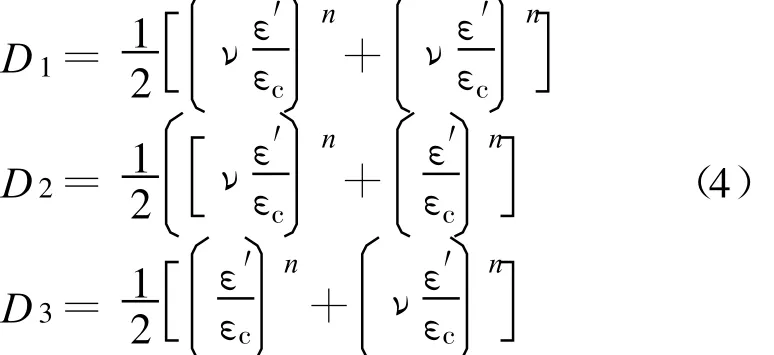
从岩石试件的单轴压缩试验观察到试件破坏的方向大体与压应力方向一致,与式(4)中D1<D2=D3相符。另外,按式(4)σ3方向也有损伤。这是因为当微裂纹出现后,微裂纹的方向并不完全是破坏时的宏观裂纹方向,初始微裂纹的方向存在一定的随机性,这也正是D1的含义。在数量上D1远远小于D2和D3。
1.2 弹脆性材料损伤本构方程
无损状态下柔度矩阵为

则由广义虎克定律及式(6)推出弹脆性损伤材料的本_构关系:

式中:D1,D2,D3为相应于3个主应力方向的损伤分量。因D1≠D2≠D3,所以共有5个独立变量。
2 基于损伤的渗流-应力耦合模型
2.1 岩体渗流有限元计算基本方程
符合Darcy定律的非均质非各向同性可压缩岩土体的三维空间非稳定渗流不考虑岩土体的压缩性(Ss=0),得到饱和稳定渗流的控制方程:
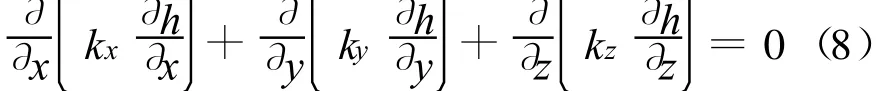
初始条件为计算开始水头场分布状态,边界条件包括已知水头边界和已知流量边界:
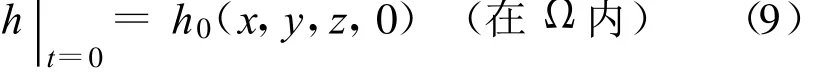
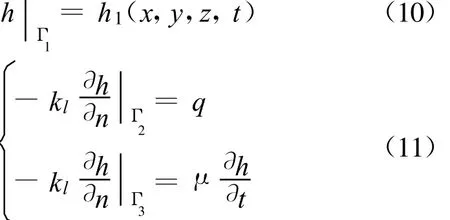
式中:kl为法向上的渗透系数;q为过潜流面的已知单位面积流量,q=0为不透水边界,q≠0为潜流边界;μ为给水度;Γ1为已知水头边界;Γ2为已知流量边界;Γ3为自由面边界。
2.2 有限元计算格式
根据变分原理,上述定解问题等价于下列泛函极小值问题:
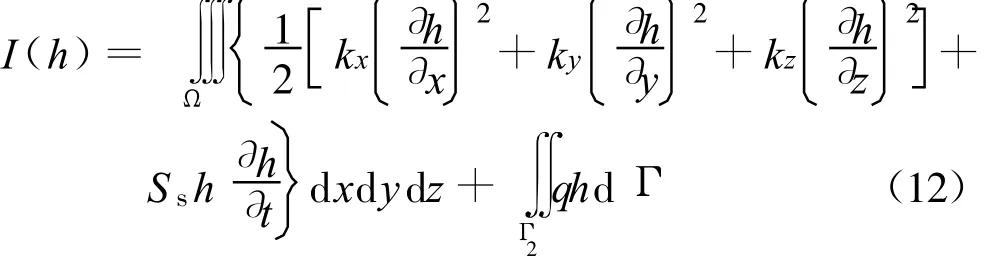
将计算域离散化,以Ie(h)表示单元体 Ωe的泛函,即
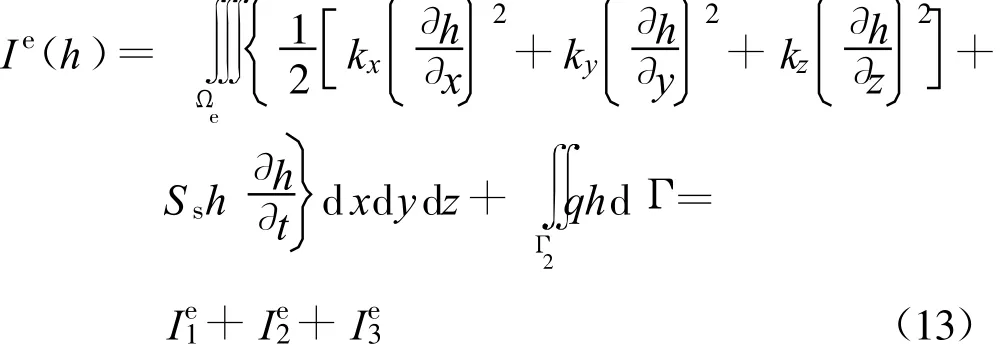
分别对任意单元e进行Ie1,Ie2,Ie3求导数和极小值变换,将所有单元的泛函求微分后叠加,并利用I(h)极小值的条件,有
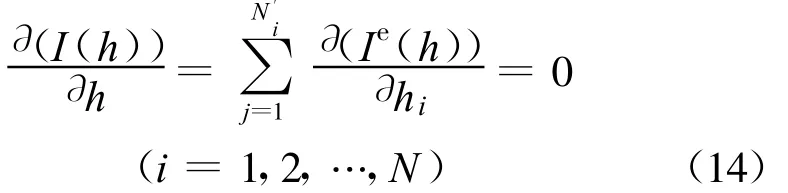
式中:N′i为以i为公共节点的单元数。
式(14)对已知水头边界节点形成常数项。通过式(14)计算以后,将常数项移到等号右端,得N个未知节点的线性代数方程组。对时间项取隐式有限差分,写为矩阵形式有
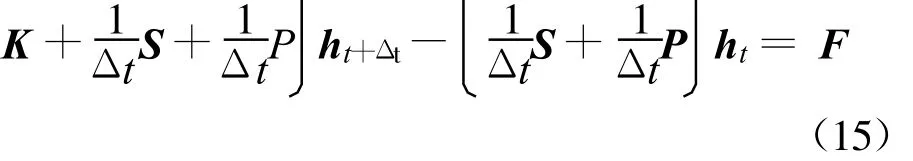
这就是有限单元法最后求解的线性代数方程。
2.3 渗流-应力耦合模型有限元网格划分与计算
有限元计算采用等参数六面体单元作为基本单元,特殊部位使用六面体单元的退化单元。标准六面体等参数单元及其局部坐标如图2所示,各种退化单元形状如图3所示。
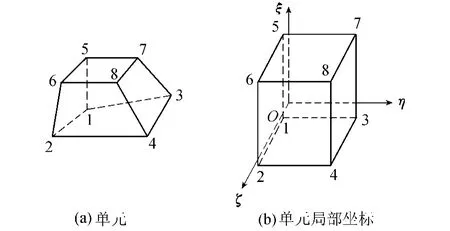
图2 六面体八节点等参数单元
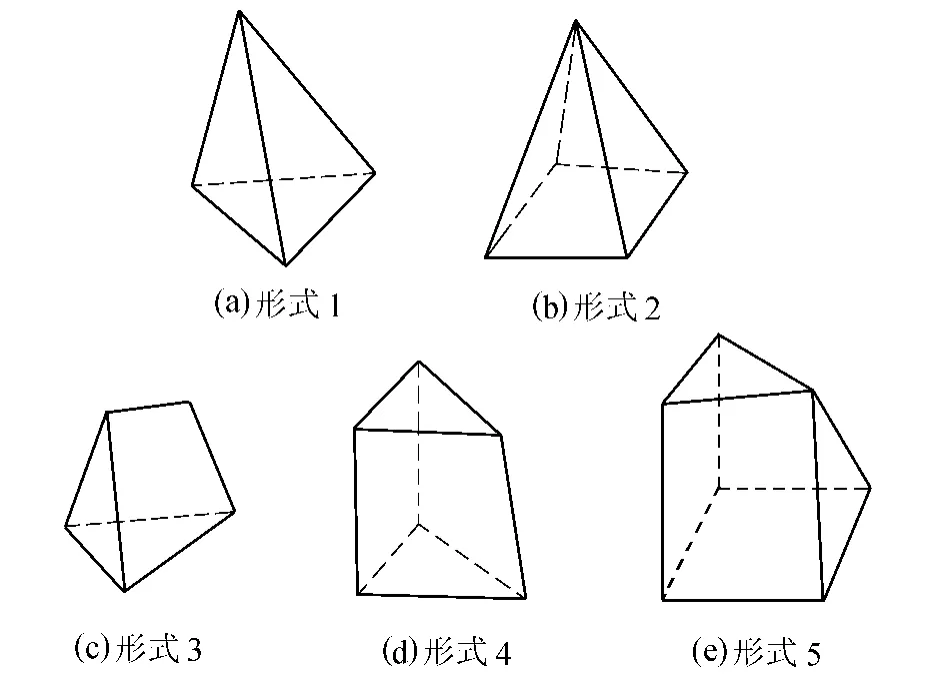
图3 六面体等参数单元的各种退化形式
对六面体八节点等参数单元的基函数进行局部坐标与整体坐标之间的变换[14],利用高斯积分法进行数值积分得
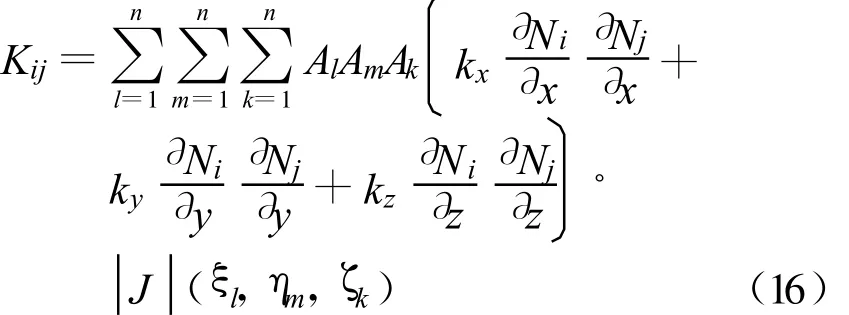
式中:Al,Am,Ak为加权系数;ξl,ηm,ζk为积分点局部坐标。
3 工程实例
某水电站坝址区河谷呈开阔不对称的V形,右岸山体雄厚,左岸为一较单薄的山脊梁,河谷深切,两岸卸荷强烈,倾倒变形严重。由于坝址区分布的较软弱岩层倾角近直立,河谷不断被侵蚀下切,河谷两岸岩体原有的平衡被破坏,两岸岩层均向河谷产生倾倒变形。为了评价坝区和山梁岩层及断层带的渗透性质、检验防渗措施的有效性,提出改良意见,制定了如下三维有限元渗流及渗透稳定计算方案。
根据前面推导的公式和有限元网格划分方法,采用南京水利科学研究院于1974年开发并不断完善的UNSS3程序进行三维渗流计算,应用于工程实践。计算采用容重替代法处理静水压力,等效节点力方法处理动水压力。三维有限元计算单元以八节点六面体(图2)为主,并包括了5种形式的退化单元(图3),以便适应复杂的地下结构与岩(断)层产状。渗流计算模型共划分27390个单元、30 080个节点。剖分后的三维网格见图4。
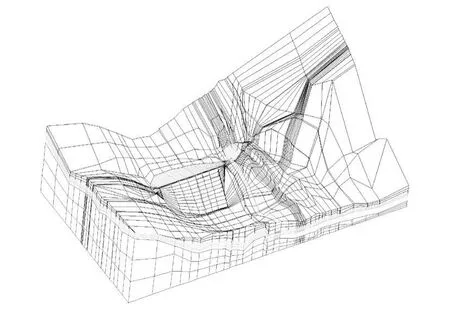
图4 三维渗流计算模型网格剖分
边界条件:三维渗流计算边界条件包括边界地下水位、地表水位、地表出渗及特殊工况的内部边界。设计拟定的特征水位如下:正常蓄水位为1408.00m,相应的下游水位为1309.80m;设计洪水位为1408.26m,相应的下游水位为1324.74m;校核洪水位为1411.92m,相应的下游水位为1327.15m。
三维渗流计算模型范围:上游边界至坝脚垂直距离约为300m;下游河床至坝脚垂直距离约为350m。左右两岸由于山高坡陡,分水岭距坝址较远,且较远处缺乏地质勘察资料,因此右岸取到右坝肩以外约500m的位置、左岸取到溢洪道以外约700m的位置作为计算域边界。左右边界以地质勘察地下水位作为已知水头边界条件进行三维渗流计算。考虑到河床部位灌浆帷幕的深度,计算模型底部边界取到1160.00m高程。三维计算模型的效果图见图5。
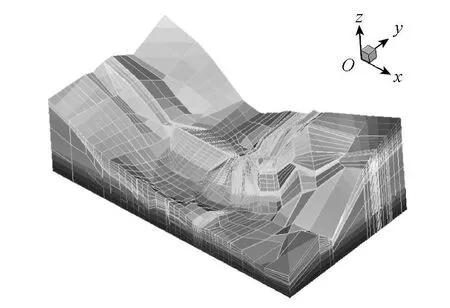
图5 三维渗流计算模型效果示意图
通过三维天然渗流场参数反演和极限工况下三维渗流数值计算(表1),得出以下结论:
a.反演计算结果表明岩层及断层带渗透性具有各向异性的性质。
b.断层带具有良好的导水性,承担的坡降小于允许比降,但流速较大,应注意防止在岩体裂隙附近出现集中渗漏造成的冲刷破坏。左坝肩附近断层(F109,F121,F122,F123)具备导水特征,因此应在上游采取有效的挡水措施,以保证渗透稳定;溢洪道部位断层(F124,F125,F126,F127)具有排水作用,不影响溢洪道的渗透稳定。
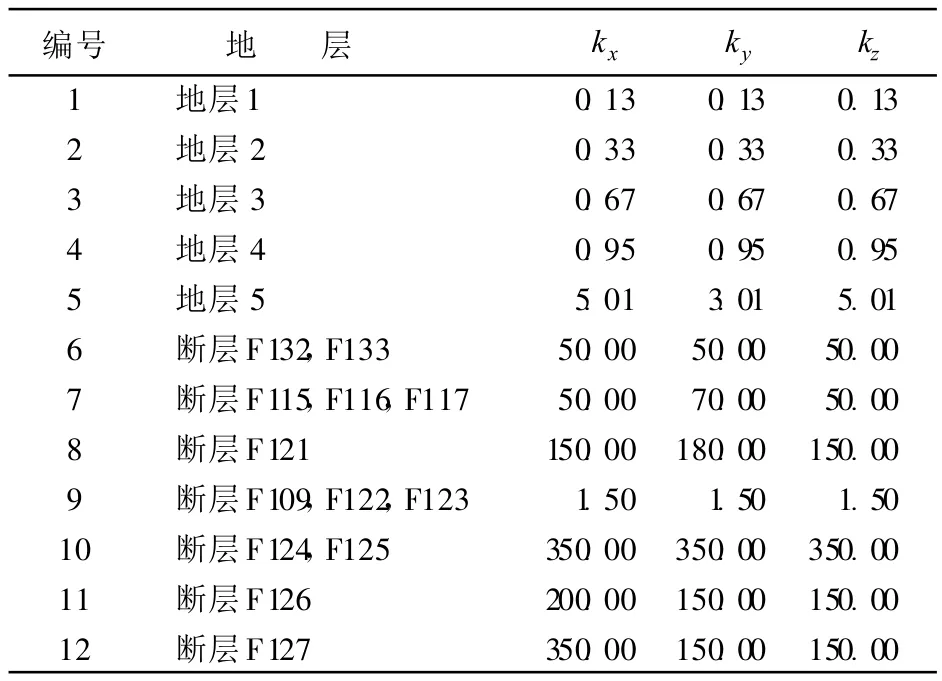
表1 反演计算得到的渗透参数 10-4cm/s
c.左岸山梁部位排水孔幕的布置能够有效地降低山梁内浸润面高度,山梁部位出逸比降不大,能够满足渗透稳定要求。
d.坝体浸润面低,由于面板及防渗帷幕承担了绝大部分水头差,坝体堆石部分的浸润面基本在建基面以上5.0m的位置,出逸点位置也不高(高程1310.62m),不存在渗透失稳问题。
e.总体渗流量偏大,右岸比左岸渗流量小,以坝肩绕渗为主。坝基渗流量以防渗帷幕底部绕渗为主,渗流量属中等。相比而言左岸渗流量较大,主要是因为山梁部位有多个强渗透断层带贯通上下游,因此该部位断层带的防渗处理应该加强。
从三维渗流有限元计算成果来看,工程渗控措施基本上是合适的,能够有效降低坝头及左岸山体的浸润面高度。但是,右岸帷幕的防渗效果不显著,建议在下阶段进行右岸帷幕的延展长度及深度的敏感性分析。总体上流量比较大,主要是左岸山梁的强导水断层带流量大,局部大流量会带来冲刷破坏问题,因此下阶段设计工作应该加强对断层带的防渗处理措施。建议取消左岸山梁引水管下游的灌浆帷幕,或在该位置建设排水孔幕,这样效果可能会更好。
4 结论与讨论
通过研究岩石破坏过程中的损伤演化规律,以及与之相伴而生的渗透性变化规律,引入随机概念描述岩石细观强度分布,得到了初始强度非均匀的岩石试样,采用应变主轴、损伤主轴和附加渗透主轴一致的原则,建立了基于应变 -损伤- 附加渗透性、反映岩石强度变化非线性特征的损伤演化模型,使得耦合计算过程物理意义清晰明了,更准确地表达了耦合过程的非线性关系。通过工程实例表明笔者建立的基于损伤的渗流- 应力耦合模型是正确可行的。
岩石的破坏是从局部开始的,但是当岩石被作为均匀介质时,基于统计方法的损伤力学很难真实地描述岩石损伤的局部化现象。基于拉应变的损伤变量既可以描述压缩状态的岩石试件,又适用于拉伸状态的岩石试件。在材料内部应力集中的区域,应变异常,损伤也相应地发生异常,这就是岩石破坏局部化的原因。但是有限元计算微元体损伤后的力学形态还需要做进一步研究,使之能够准确模拟损伤的局部化扩展。
岩石损伤的最后结果是岩石断裂破坏,基于连续介质力学体系的损伤力学还不能准确地描述岩石的断裂过程以及断裂状态。将损伤和断裂理论相结合来研究岩石的破坏过程将是值得研究的技术方法。在这一点上,损伤因子和断裂指标的结合以及由损伤到断裂的物理机制将是断裂损伤联合研究的重点,也是难点,还有待于深入研究。
:
[1]黄秋枫,胡海浪.渗流-应力-损伤耦合研究现状[J].灾害与防治工程,2009,66(5):27-34
[2]杨天鸿,唐春安,徐涛,等.岩石破裂过程的渗流特性:理论、模型与应用[M].北京:科学出版社,2004:32.
[3]张文捷,程荣兰,詹美礼,等.岩体渗流的一种改进数学模型[J].河海大学学报:自然科学版,2010,38(1):52-57.
[4]王环玲,徐卫亚,童富国.泄洪雾雨区裂隙岩质边坡饱和-非饱和渗流场与应力场耦合分析[J].岩土力学,2008,29(8):2397-2403.
[5]宋晓晨,徐卫亚.裂隙岩体渗流模拟的三维离散裂隙网格数值模型(Ⅰ):裂隙网格的随机生成[J].岩石力学与工程学报,2004,23(12):2015-2020.
[6]卢刚,周志芳.降雨入渗下互层状裂隙岩体非饱和渗流分析[J].岩土工程学报,2008,30(9):1399-1403.
[7]黄勇,陈静.岩体裂隙介质各向异性耦合模型研究[J]河海大学学报:自然科学版,2009,37(2):171-174.
[8]王俊光,梁冰.渗透动水压力作用下裂隙岩体渗流与应力耦合分析[J].辽宁工程技术大学学报,2009,28(4):178-180.
[9]陈祖安,伍向阳.岩石渗透率随静水压力变化的关系研究[J].岩石力学与工程学报,1995,14(2):155-159.
[10]ODA M T,TAKEMURA A,AOKI T.Damage growth and permeability change in triaxial compression tests of india granite[J].Mechanics of Materials,2002,34:313-331.
[11]周维垣,剡公瑞,杨若琼.岩体弹脆性损伤本构模型及工程应用[J].岩土工程学报,1998,20(5):54-57.
[12]PLESHA M E.Constitutive modeling of rock joints with dilation[C]//26th US Symposium on Rock Mechanics.Rapid City,SD(USA):American Rock Mechanics Association,1985:387-392.
[13]安民,俞茂宏,吴熹,等.广义双剪屈服准则在岩石力学中的应用[J].岩土力学,1991,12(1):17-26.
[14]魏泽光.三维有限元法中等参数六面体单元的单元分析[J].高等学校计算数学学报,1979,1(1):3-9.

