动态规划逐次渐近法在江都三站叶片全调节优化中的应用

仇锦先,程吉林,张仁田,张礼华,龚 懿

(1.扬州大学水利科学与工程学院,江苏扬州 225009;2.江苏省水利勘测设计研究院有限公司,江苏扬州 225009)

江都三站是我国南水北调东线源头泵站江都站之一,进行站内多机组优化是研究站群优化运行的前提。目前,国内已有学者对江都站的优化运行进行了研究,如马文正等[1]、陈守伦等[2]采用动态规划法求解了抽水流量一定及日抽水量一定的情况下江都站的最优运行方式;陆一忠[3]采用逆序增量动态规划法求解了总抽水流量一定、抽水功率最小时江都站的联合优化调度过程;冯晓莉等[4]应用遗传算法求解了日抽水量一定的情况下水泵变角和定角时的江都站最优运行方案等,但均未涉及单站多机组变工况优化运行计算方法的比较研究。笔者在江都站已有优化运行理论的基础上,结合江都三站叶片全调节优化的实例,着重对双决策变量非线性优化问题的求解方法进行分析探讨,即采用动态规划逐次渐近法[5-8]实现了优化运行过程,同时采用基于整数线性规划的试验选优法对计算结果进行验证,为站内多机组变工况优化计算提供了新的求解方法。

1 数学模型的建立

考虑长江潮位、峰谷电价等影响因素,以江都三站运行机组耗电费用最小为目标函数,以提水总量、额定功率等为约束条件,建立站内多机组叶片全调节优化运行数学模型。

a.目标函数

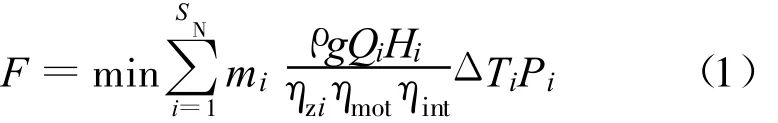
式中:F为站内运行机组耗电费用,元;SN为时段总数,根据分时电价划分;mi为第i时段开机台数,台,0≤mi≤Jz,Jz为站内机组台数(机组型号相同),台;ρ为水的密度,kg/m3;g为重力加速度,m/s2;θi为机组第i时段叶片安放角度,(°);Qi为机组第i时段的提水流量,m3/s,当扬程、转速一定时,Qi为θi的函数;Hi为第i时段的平均扬程,m;ΔTi为第i时段的开机时间,h;Pi为第i时段的分时电价,元/(kW·h);ηzi为机组第i时段的装置效率;ηmot,ηint分别为机组的电动机效率和传动效率。

b.约束条件

提水总量约束:

机组运行功率约束:

式中:Wd为机组24h运行的提水总量,m3;Ni为机组第i时段实际运行功率,kW;Ne为电机额定功率,kW。

2 模型的求解

根据前述建立的数学模型,站内多机组优化属于多机组、多阶段、双决策变量非线性系统优化问题。这里采用动态规划逐次渐近法确定各时段的最优开机台数及叶片安放角度。

2.1 动态规划递推方程与状态转移方程

阶段变量为i,决策变量为开机台数mi、叶片安放角度 θi,状态变量为阶段提水量 λi,则对应的递推方程和状态转移方程如下:

i=1时递推方程为

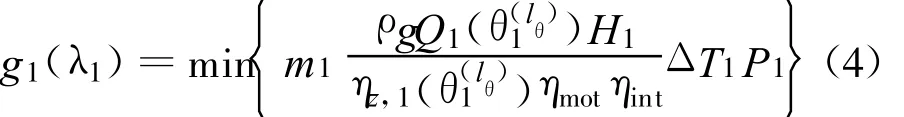
λ1在其对应可行域内离散:λ1=0,W1,W2,…,Wd;决策变量满足 :0 ≤m1Q1(θ(lθ)1)ΔT1≤λ1,θ(lθ)1在其可行域内第lθ种离散取值。

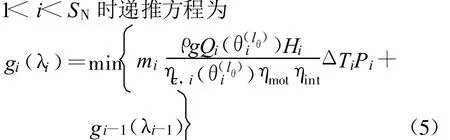
λi在其对应可行域内离散:λi=0,W1,W2,…,Wd;决策变量满足:0 ≤miQi(θ(lθ)i)ΔTi≤λi,θ(lθ)i在其可行域内第lθ种离散取值。

状态转移方程为

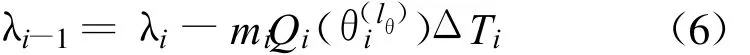
i=SN时递推方程为

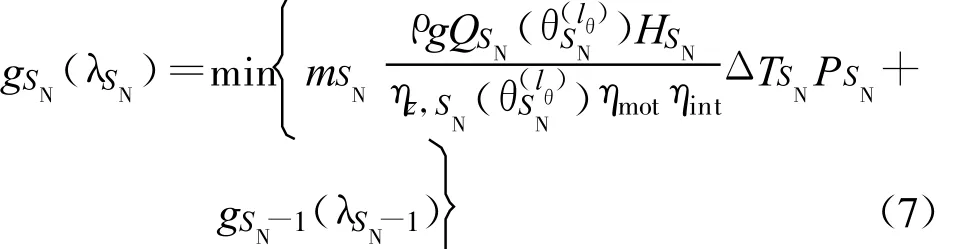
λSN=Wd,Wd+ΔW(ΔW为某一大于零的水量);在其可行域内第l种离散取值。θ

状态转移方程为

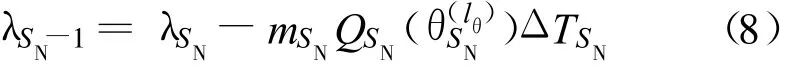
2.2 动态规划逐次渐近法的基本步骤

动态规划逐次渐近法由Bellman[7-8]提出,简称为DPSA法,其在多机组叶片全调节优化中的基本步骤为:先假设各阶段叶片安放角度已知,进行变台数优化计算,确定目标优化值及相应各阶段开机台数组合方案;再以各阶段优选的开机台数为已知量,进行叶片全调节优化计算,确定本次目标值及相应各时段叶片安放角度组合方案,完成1次循环,然后以迭代形式重复执行以上过程,直到程序获得某种程度的收敛为止。

3 计算结果与分析

3.1 基本资料

江都三站有10台2000ZLQ13.7-7.8型泵,额定转速ne=214.3r/min,设计叶片安放角度为+2°,水泵的性能曲线见文献[9]。考虑分时电价和大型泵站不宜频繁开停机的要求,将全天分为9个时段;考虑江都站长江典型潮位的影响,选取日平均扬程5.8m进行计算;分时电价根据江苏省物价局现行规定确定,各时段平均扬程及分时电价见表1。机组叶片安放角度在其可行域内离散:θi=-6°,-4°,-2°,-1°,0,+1°,+2°,+4°。

表1 各时段平均扬程及分时电价

3.2 计算结果

在日均扬程5.8m、不同提水负荷情况下,采用动态规划逐次渐近法求解江都三站多机组叶片全调节优化模型,计算结果见表2。同时采用基于线性规划的试验选优法对该优化模型进行求解,即以时段为因素,叶片安放角度为水平,构建9因素8水平L64(89)型正交表,将模型的求解转化为求解单决策变量线性规划问题,求出64次试验水平组合方案的目标值及相应9时段开机台数组合方案;再通过正交分析,得到各时段叶片安放角度最优组合方案;在此基础上,利用线性规划求解方法求出系统最优目标值及相应各时段开机台数最优组合方案,计算结果见表2。

表2 江都三站多机组叶片全调节优化计算结果

上述2种求解方法计算所得的单位提水费用比较见表3。

3.3 结果分析

a.根据表2,在不同运行负荷情况下,动态规划逐次渐近法与基于线性规划的试验选优法计算所得的优化调度过程总体保持一致。为使运行机组耗电费用最小,在低电价、低扬程时尽可能多提水,即叶片安放角度一般在可行域内调至较大值,并使多机组投入运行;而在高电价、高扬程时尽可能少提水,即叶片安放角度在可行域内调至较小值,并使少机组投入运行,甚至不开机。根据表3,以单位提水费用作为评价指标,在不同运行负荷情况下,2种计算方法所得的单位提水费用非常接近,偏差率均小于0.5%。

b.采用动态规划逐次渐近法可以将多决策变量动态规划问题转化为一系列单决策变量问题,从而大幅度节省了计算机存储量和计算时间,实例应用表明,该方法计算收敛速度较快。

4 结 论

a.针对站内多机组叶片全调节双决策变量动态规划问题,以江都三站为例,采用动态规划逐次渐近法进行求解,确定各阶段最优开机台数及叶片安放角度,实现了站内叶片全调节优化调度过程,同时采用基于线性规划的试验选优法对其优化结果进行验证,结果表明计算结果可靠,所采用的方法可行。

表3 2种方法单位提水费用比较

b.为了验证动态规划逐次渐近法所得解的最优性,选取不同的起始廊道,观察程序目标值是否收敛到同一值。采用了2种途径改善初始轨迹,一是直接改变某一决策变量的初始赋值;二是改变叶片安放角度和开机台数的决策次序。

c.动态规划逐次渐近法同样适用于站内多机组变频变速优化运行、叶片全调节变频变速组合优化运行问题的求解,丰富了站内多机组变工况优化运行理论,同时为并联泵站、梯级泵站子系统优化模型计算方法的选择提供了参考。

:

[1]马文正,丘传忻,贺贵明.泵站运行的优化调度[J].水利学报,1993(3):35-41.

[2]陈守伦,芮钧,徐青,等.泵站日优化运行调度研究[J].水电能源科学,2003,21(3):82-83.

[3]陆一忠.大型泵站优化调度及其经济问题探讨[D].南京:河海大学,2003.

[4]冯晓莉,仇宝云,黄海田,等.南水北调东线江都排灌站优化运行研究[J].水力发电学报,2008,27(4):130-134.[5]程吉林.大系统试验选优理论和应用[M].上海:上海科学技术出版社,2002.

[6]COOPER L,COOPER M W.Introductiontodynamic programming[M].张有为,译.北京:国防工业出版社,1985.

[7]BELLMAN R E.Introduction to the mathematical theory of control processes[M].New York:Academic Press,1967.

[8]BELLMAN R E,DREYFUS S E.Applieddynamic programming[M].Princeton:Princeton University Press,1962.

[9]仇锦先,程吉林,张仁田,等.江都站不同型号机组叶片全调节优化运行效果分析[J].南水北调与水利科技,2009(6):85-89.