一维数学模型在堤前滩面短期演变计算中的应用

张景新,王 颖,王 伟,寇 军,王佳飞,刘 桦

(1.上海交通大学船舶海洋与建筑工程学院,上海 200240;2.上海化学工业区物业管理有限公司,上海 201507)

沿海地区夏季频繁的台风对海岸防护工程有诸多危害,涉及越浪、护岸结构的破坏及堤身的稳定等。台风引起的风浪在滩面上传播,伴随着波浪的破碎,引起滩面上大量的床沙起动、悬浮及输移。滩面冲淤变化不仅影响着波浪的传播、爬高及越浪,同时也影响着堤身结构的稳定,甚至引起海岸灾害。

鉴于海岸防护工程的重要性,波浪作用下滩面冲淤演变的研究一直以来备受关注,国内外近年来已有大量的研究成果[1-4],涉及试验研究及数值模拟。试验研究借助于大型水槽设备的开发及测量手段的不断完善,已取得了丰硕的研究成果[4]。数值模拟手段在海滩输沙的计算中也发挥着重要的作用。近年来,复杂流体运动模型或水沙两相流模型在海岸带潮流场、波浪场及泥沙运动的研究中逐渐得以发展,在水沙运动的机理性研究中发挥着重要的作用[3,5]。但对于实际海岸工程而言,大型数值模型的开发及应用还难以达到工程实际应用的程度。早期发展的海岸带横向输沙的一维数学模型形式相对简单,计算工作量较小,借助于实测资料及合理的经验系数的选取,该类模型在实际工程应用中具有一定的适用性。一维数学模型应用中的首要问题是确定横向输沙率,目前已有众多输沙率计算方法[6-7]。依据输沙的动力因素不同,研究者将泥沙在空间上分为波浪上涌带和波浪浅化带及破碎带分别加以考虑[7]。泥沙输沙率计算公式繁多,如何选择或发展适合特定水动力条件下的输沙率公式非常重要。一维数学模型涉及的输沙率计算公式多为经验型公式,但借助于适当的实测资料及经验系数的选取,往往可获得较满意的计算结果。

笔者建立了波浪作用下滩面演变的一维数学模型,波浪场模拟采用波浪能量守恒方程,该方程计入了波浪破碎效应。波浪模型给出波参数的空间分布,应用于输沙率的计算。横向输沙率计算公式参考了众多研究成果,计入了波浪上涌带泥沙输沙率、波浪浅化带及破碎带输沙率及波生流对泥沙输运的作用。将该模型应用于杭州湾某海防工程堤前滩面的冲淤演变计算,模拟了某次台风过境期间风浪所引起的滩面冲淤变化。通过数值模拟验证了该模型的精度,分析了若干影响因素及该模型的适用性。

1 数学模型

1.1 波浪场计算

文中波浪场的计算基于规则波,通过波浪能量(或波作用量)守恒方程的求解,获得波浪要素的空间分布。近岸水域波浪运动受地形等因素的影响,运动形式复杂,浅化、折射及绕射现象并存,笔者仅考察入射波浪在横向的传播演化及其所引起的横向输沙,将控制方程简化为横向的一维模型。近岸带水体运动受到诸多因素的影响,如床面摩阻作用随水深的减小逐渐显著。而波浪破碎是该水域波浪运动的显著特征,本文模型仅概化了破波带内波浪运动的破碎效应,控制方程如下:

式中:Cg(x)为波浪群速度;E(x)为单位波长的波能;Hw(x)为波高的空间分布;Dw(x)为由波浪破碎引起的波能耗散项;W为破波因子函数(W建立了空间波高与当地水深的关系,通过设定破波指标可将波浪破碎这一物理过程模式化,大量应用成果表明该处理方法具有相当广泛的适用性),本文破波因子函数计算式来源于文献[8];K为计算系数;d为当地水深;γ为破波指标,γ=0.73。

利用有限差分法求解上述波浪能量守恒方程,求得波浪参数的空间分布,进而可计算床面应力等物理量,并进一步用于计算横向输沙率。

1.2 床面演化控制方程

床面横向演化的一线方程给出了局部床面高程的时间变化与输沙率横向变化的关系,表达式如下:

式中:z为床面高程;ε为床沙孔隙率;ρs和 ρ分别为泥沙的密度和水的密度;g为重力加速度;q为输沙率;qR为波浪上涌带的输沙率;qw为波浪浅化带及破碎带内的输沙率。

海岸带横向输沙率的空间分布如图1所示。图中区域1,2,3分别代表破波带外、破波带和波浪上涌带;xB,xR,xM分别为破波点的横坐标、上涌带的输沙率峰值点的横坐标和波浪最大爬升高度处的横坐标;dB,dR分别为xB,xR处的水深。观察图1可知,破波带(区域2)内的输沙强度最大,波浪上涌带的输沙强度随着波浪的爬升逐渐减弱。利用迎风格式的有限差分法数值求解式(2),而式(2)的求解首先需要给出横向输沙率的计算表达式。

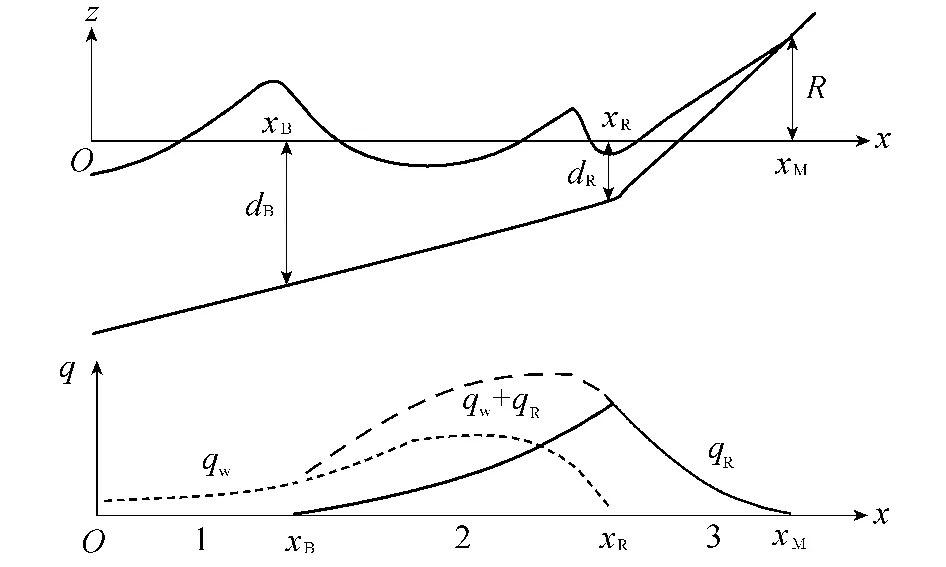
图1 近岸带横向输沙强度空间分布[7]

1.3 海岸带横向输沙率

海岸带横向输沙率按空间分布可分为2部分,即波浪上涌带的输沙率qR和波浪浅化带及破碎带内的输沙率qw。参考已有的研究成果[7-8],分别给出各输沙率的计算表达式。海浪上涌带的qR计算公式如下:

式中:βeq为床沙平衡角;β为床面坡度;c1为系数,c1=10-3～10-1;R为波浪爬升高度;Hs0为入射波的有效波高;L0为深水波波长。

上涌带外侧qR值通过式(4)计算得到:

式中:c3为系数,c3=0.2～0.3。

浅化带及破波带内的波浪输沙率qw可分为推移质输沙率qb和悬移质输沙率qs,参考已有的研究成果[3,7],分别给出各自的计算表达式:

式中:εb为推移质输沙效率 ,εb=0.1;εs为悬移质输沙效率,εs=0.01;Φ为床沙颗粒的内摩擦角,tan Φ=0.6;fw为波浪摩阻系数;Ud为水深平均的离岸流速;F和B分别为床面摩阻和波浪破碎引起的动能耗散率;T为波周期;Uw为波浪边界层处水质点运动速度幅值;z0为床面粗糙尺度;ωs为泥沙沉速;d50为床沙中值粒径。

离岸流体运动主要分布于下层水体,该流动与向岸的波浪场质量输移运动和破碎波引起的上层水体的向岸运动相平衡,Ud可由式(7)计算:

式中:c为波浪相速度;E为波能。

悬移质输沙率计算表达式中F及B的计算参考相关研究成果[7]:

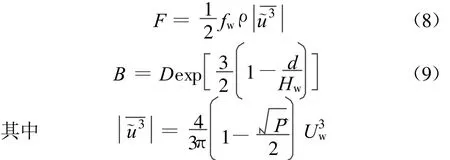
2 模型应用及讨论

将模型应用于杭州湾某海防工程堤前滩面冲淤演变的数值模拟研究中,该海防工程位于杭州湾北岸,工程位置及地形测量断面位置见图2(图中符号G代表断面)。2005年“麦莎”台风前后,分别开展了堤前水下地形的测量工作,2次测量前后间隔大约3个月。2次局部地形的变化主要由此次台风过境期间的风浪所引起。首先根据现场实测资料确定计算水文条件,台风风向ESE,取入射波的有效波高Hs0=2.7m,相应周期T=6.5s,堤前平均潮位 η0=2.0m,波向由实测资料确定为正向入射。模型计算波参数取相应的有效波参数,计算历时24h(实际台风过境历时约72h)。堤前滩面床沙中值粒径d50=0.03mm,将2005年5月地形作为初始地形,采用所设定的水文参数,模型给出了此次台风过境期间风浪所引起的冲淤变化量。该海防工程堤前建有混凝土护岸的缓坡,故在输沙率的计算中未考虑波浪上涌带的泥沙输沙率。

测量资料给出了沿岸4个固定断面的地形资料,将各断面的模拟结果与实测资料比较,如图3所示。图3分别给出了4个固定断面2005年5月和8月的实测地形值和台风后滩面地形的模拟值,x轴负向为外海方向,正向为堤身方向。计算结果显示在堤脚的邻近区域各断面普遍出现滩面冲刷,而离岸方向普遍出现淤积。实测结果显示在邻近堤脚的区域内滩面冲刷明显,离岸方向冲淤幅度减弱。计算值与实测值在邻近堤脚的区域吻合较好。分析流场动力因素,随着水深的减小,入射波波高逐渐增大,直至破碎。破波带内波浪对泥沙的输运起着非常重要的作用,而在远离堤脚的水域,潮流作为泥沙输运的动力因素逐渐增强。分析该水域水文实测资料,潮流运动表现为沿岸往复流动,与波向近似正交,其输沙方向为沿岸。本文模型仅关注了波浪作用下的泥沙横向输运,未计及潮流对泥沙输运的影响。以G1断面为例,模拟结果显示该断面内床沙的冲淤总量平衡,而实测值显示该断面的总冲刷量大于淤积量,意味着部分起悬泥沙可能为潮流所输运,表现为沿岸输沙。除潮流影响外,破碎波引起的沿岸流动也是重要的动力因素之一。沿岸流在浅水近岸处受地形等因素影响较弱,泥沙输沙方向基本维持在断面内。远离堤脚,随着水深的增加,地形等影响作用减弱,沿岸流动增强,沿岸输沙强度渐增,这一因素未计入本模型,也是影响远离堤脚处计算偏差渐增的可能原因之一。

图2 工程位置图及地形测量断面位置

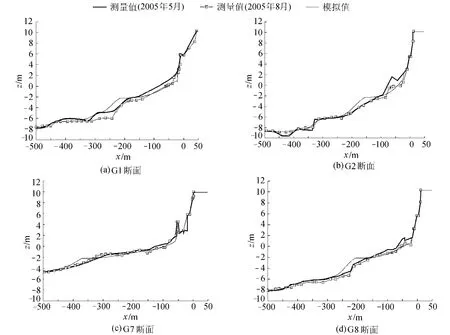
图3 滩面地形冲淤变化

3 结 语

海岸带横向泥沙输运的一维数学模型以其形式简单、计算高效等特点,具有较高的实用性。模型成功应用的前提是横向输沙率的准确计算。海岸带流动条件复杂,波浪的浅化、破碎及上涌都对泥沙运动起着重要的作用,不同输沙形式是由不同的动力因素决定的。面对种类繁多的输沙率公式,还有待分析总结及发展更适合的计算模型。深入研究该水域的流体运动,量化各流动物理量是改进模型的前提。此外,如文中提到的这类工程设施,不仅需要考虑风浪,还需考虑潮流作用,这方面的工作还有待深入。并且,文中模型应用于实际海岸的床面冲淤,针对规则波,而实际风浪为随机波列。虽然对于近岸床面的冲淤模拟结果较好,但仍需进一步研究随机波作用下的滩面冲刷。

:

[1]RAKHA K A,DEIGAARD R,BROKER I.A phase-resolving cross shore sediment transport model forbeach profile evolution[J].Coastal Engineering,1997,31(4):231-261.

[2]SPIELMANN K,ASTRUC D,THUAL O.Analysis of some key parametrizations in a beach profile morphodynamical model[J].Coastal Engineering,2004,51(10):1021-1049.

[3]LEONT'YEV I O.Short-term shoreline changes due to crossshore structures:a one-line numerical model[J].Coastal Engineering,1997,31(1):59-75.

[4]van RIJN L C.Prediction of dune erosion due to storms[J].Coastal Engineering,2008,56(4):441-457.

[5]CHRISTENSEN E D,WALSTRA D J,EMERAT N.Vertical variation of the flow across the surf zone[J].Coastal Engineering,2002,45(3):169-198.

[6]钱宁,万兆惠.泥沙运动力学[M].北京:科学出版社,1983:270-359.

[7]LEONT'YEV I O.Numericalmodeling of beach erosion during storm event[J].Coastal Engineering,1996,29(2):187-200.

[8]KIRBY J T,DALRYMPLE R A.Modeling waves in surf-zones and around islands[J].Journal of Waterway,Port,Coastal and Ocean Engineering,1986,112(1):78-93.