基于MFDA-PCA的间歇过程故障诊断方法研究

关明礼,原忠虎

(沈阳大学 信息工程学院,辽宁 沈阳 110044)

基于MFDA-PCA的间歇过程故障诊断方法研究

关明礼,原忠虎

(沈阳大学 信息工程学院,辽宁 沈阳 110044)

针对传统MPCA间歇过程故障诊断方法存在的在线数据不完整及实时性差缺陷,提出一种基于MFDA-PCA间歇过程的在线批次故障诊断方法.通过MFDA对在线批次正常部分与历史批次进行相似度分析,利用相似度最优的批次建立PCA模型,对在线批次数据进行实时分析,完成对整批生产过程在线监控及故障诊断的任务.最后以青霉素发酵仿真实验验证了该方法的有效性和快速性.

MFDA;PCA;间歇过程;相似度分析

在当代工业生产中,间歇过程以其独特的生产方式和产品特性受到了人们的高度重视.从间歇过程故障诊断方法来看,Nomikos和MacGregor提出的多向主元分析法和多向最小二乘法(Multiway PCA/Multiway PLS)[1,2]应用最为成功.这种方法首先对历史批次数据进行预处理,将历史三维数据转变为二维形式,然后再利用传统的PCA/PLS方法进行建模分析.后来,为了避免预估计未来信息,相关学者提出了一系列改进的方法,如:滑动窗口 MPCA[3]和步进式MPCA[4]方法等.通过采用多个小窗口将整个历史批次信息进行分割,提高了故障诊断的准确性,并在实践中收到了良好的效果,但实时性要差一些.本文提出一种基于MFDA-PCA的间歇过程故障诊断方法,通过对正常生产过程进行相似度分析,得到最优匹配结果,利用所建立的PCA模型对在线批次数据进行故障诊断.

1 费舍尔判别分析法(FDA)基本原理

费舍尔判别分析法 (Fisher Discriminate Analysis,FDA)[5]是广泛应用于模式识别领域的一种分类方法.它通过寻求一系列能代表数据变化最优的特征方向,在其方向上投影,实现类与类之间的相互分离.

现取一训练集样本 X∈Wn×m,其中 n为样本总数目,m为观测变量数.n中分为 p个模式类,即ω1,ω2,…,ωp.第 j类样本数记为nj.利用任意样本中的元素 xi定义一系列矩阵如下:

2 MFDA-PCA故障诊断模型的建立

2.1 数据的预处理

所谓MFDA方法就是在利用普通的FDA方法建模分类前,先对历史三维数据进行预处理.由于间歇过程历史数据包含批次问题,历史数据可表示为一个三维矩阵 X(I×J×K),其中 I代表批次,J代表每个批次的变量数,K代表采样时刻.为了采用FDA方法进行相似度分析计算,先将数据集 X按照不同的批次进行切割,并沿其方向展开,得到新的二维数据矩阵=(I K×J).这样做的目的就是对新矩阵能够应用传统的FDA方法进行建模.为了更加直观地看出MFDA和传统FDA之间的联系,将间歇过程典型的三维变量由应用传统FDA方法的二维变量替换,即:类 j→批次 I,每类观测值个数 nj→采样时刻 K,测量变量数 m→变量J,MFDA的间歇过程故障诊断模型就转化成了普通FDA的诊断模型.具体展开形式见图1.

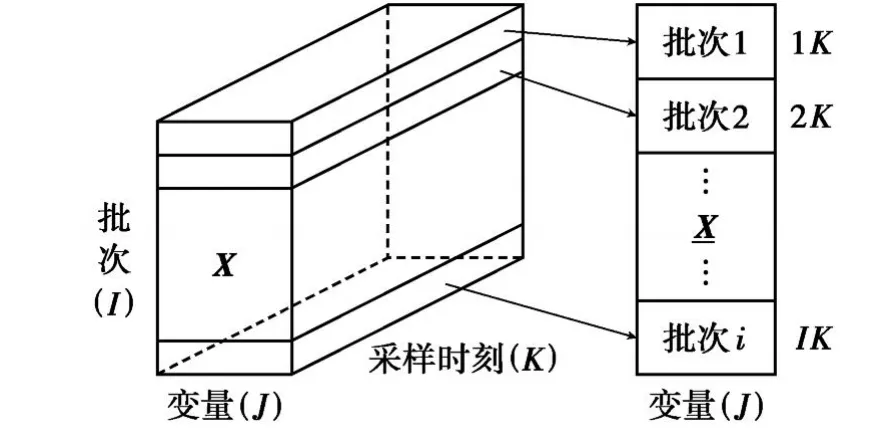
图1 MFDA三维数据展开示意图

2.2 MFDA相似度分析

数据预处理后的二维矩阵经过式(1)的计算,求出判别函数所需要的所有变量,包括:类内均值、类内离散度矩阵Sj以及变换矩阵Wa.测试样本FDA模型中第 j个类的判别函数[6]为

其中,gj(x)表示测试批次的每个采样点对于某一历史批次对应时刻的判别值,Wa是由广义特征向量Wk通过降维的形式构成的矩阵,Sj为某一批次的内部离散度矩阵.本文从中选取每个类所有时刻 gj(x)的和的最小值作为相似度最优的判别依据,表达式为

其中,sum(gj(1,1…k)(x))表示测试样本和历史库任意一类样本中所有时刻的判别函数值的和; sum(gj(1,1…k)(x))表示测试样本和第 j个类样本所有时刻的判别函数值的和.

2.3 MFDA-PCA在线故障诊断模型

基于历史库中每个类的信息,建立各自的PCA模型,对在线数据中未出现故障部分进行FDA相似度分析;调用相似度最优类的PCA模型对在线数据进行实时监测,同时确定该类数据的 T2和 S PE统计控制域;对于超出控制域的时刻进行各变量的贡献图分析,找出出现异常的位置,完成故障诊断工作.T2和 S PE的统计控制域[7]可分别表示为

其中,k为降维后的主元个数,n为样本数, Fk,n-1,α表示对应于检验水平为α、自由度为 k、n-1条件下的 F分布值.

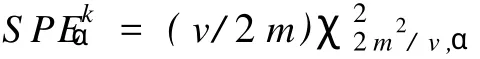
3 实验仿真

3.1 离线建模阶段批次相似度分析

Pensim 2.0[8]是青霉素仿真实验平台,它为研究间歇过程的故障诊断方法提供了良好的仿真环境.该平台对青霉素发酵过程不同操作条件下的微生物浓度、CO2浓度、pH值、青霉素、溶氧度等16个变量进行仿真.每个批次生产总耗时400 h,其中包括50 h的菌种培养阶段和350 h的补料阶段.本实验选取16个变量进行监控,采样时间间隔1 h,并从整个生产过程历史数据集中选取10批次数据,即 m=16,n=400,j=10.

在离线建模过程中,MFDA相似度分析测试实验的步骤是:首先从Pensim仿真数据库中任意选取10批正常数据,其初始条件和操纵变量都已知并在正常范围内波动,做好标记;再从这10批数据中选出初始化条件和操纵变量完全一样的3批作为测试数据,依次记为测试批次1、测试批次2和测试批次3;同时观测每个测试批次所有时刻对应于历史库中10个批次数据的 gj(x)值,将这些值按批次方向进行求和并统计成表,见表1.

表1 相似度判别函数 sum(gj)值

分析得出,测试批次1、2、3分别和已知批次中的2、10、3取得最优化相似度.

3.2 青霉素发酵过程的在线故障诊断

分别在批次3和10的生产条件下重新生产两批青霉素产品,并在生产中分别加入两种不同类型的故障扰动信号,验证MFDA-PCA的故障诊断能力.具体引入的故障类型如下:

(1)故障类型1.批次3的生产到200 h时,人为对通风率(变量1)引入一个幅度为当前变量-1.5%的阶跃扰动信号,并在250 h后结束此扰动信号.在扰动信号加入反应过程时,整个批次的生产过程发生了故障,并对其他变量也产生影响.

图2 故障1在后300 h的 T2统计图

图3 故障1在后300 h的 SPE统计图

图4 故障1各变量对 T2的诊断贡献图

图5 故障1各变量对 SPE的诊断贡献图

(2)故障类型2.批次10的生产到300 h时,人为对底物流加速率(变量2)引入1.5%的斜坡信号,直至反应结束.调用历史库中批次10来监控在线批次的生产.具体 T2和 S PE的统计监控图和各变量对故障发生时的贡献见图6～图9.

图6 故障2在后300 h的 T2统计图

图7 故障2在后300 h的 SPE统计图

图8 故障2各变量对 T2的诊断贡献图

图9 故障2各变量对 SPE的诊断贡献图

由于前100 h为FDA模型的相似度分析,所以在线监控及故障诊断是从101～400 h.从图2和图3看出,在线生产批次在203～250 h处大大超出了原始批次95%的 T2和 S PE控制限,被视为出现了故障,而且及时准确地测量了出来;而其他时刻都在被控范围内,属于正常生产过程.图4和图5分别表示的是对那些超出 T2和 S PE范围时刻的变量进行贡献图分析,图4第1个变量(通风率)产生的贡献率最大,属于故障类型1.

对于故障类型2来说,实际发生时刻为第300 h,而通过图6的 T2统计图观测到故障超限时刻为第 325 h左右,图 7的 S PE统计图为305 h左右.图8描述了故障发生时刻变量3(底物流加速率)对 T2的贡献最大.

通过比较传统MPCA方法和本文应用的MFDA-PCA方法得出故障1和故障2诊断的滞后时间显示(见表2、表3),本文采用的方法要优于传统MPCA方法.

表2 故障类型1被两种方法所诊断的滞后时间

表3 故障类型2被两种方法所诊断的滞后时间

4 结 论

分析结果表明,MFDA-PCA对于故障类型1的阶跃扰动信号来说,故障检测效果和实时性非常理想;对于故障类型2的斜坡扰动信号来说, T2和 S PE的检测时刻都有一定的延时.但无论是 T2还是 S PE的检测故障时刻,本方法都较传统MPCA法及时,且诊断效果也较好.

这种新型的间歇过程故障诊断方法的优点在于模型简单、运算速度快,适合于反应过程较短、监控时间间隔较小的间歇过程,且不需要预估计当前时刻以后的值,大大提高了监视的精度和故障诊断的准确度.不足之处在于对历史批次和在线批次的初始条件和操作条件有着苛刻的要求,随着生产的进一步进行,相似度最优的批次可能发生变化,影响在线批次生产过程中故障的诊断结果,这是以后相关研究中工作中需要改进的地方.

[1] Nomikos P,MacGregor J F.Monitoring batch processes using multi-way principal component analysis[J].AIChE Journal, 1994,40(8):1361-1375.

[2] Nomikos P,MacGregor J E.Multi-way partial least squares in monitoring batch process[J].Chemometrics and Intelligent Laboratory Systems,1995,30(1):97-108.

[3] Chen J,Liu K.On-line batch process monitoring using dynamic PCA and dynamicPLS models[J].Chemical Engineering Science,2002,57(1):63-75.

[4] He N,Xie L,Wang S Q,et al.Fermentation batch process monitoring by step-by-step MPCA[C]∥ International Conference on Advanced Control ofChemicalProcesses, HongKong:[S.n.],2004:70-78.

[5] 陈亚华,蒋丽英,郭明,等.基于多向Fisher判别分析的间隙过程性能监控[J].吉林大学学报:信息科学版,2004,22 (4):384-387.

[6] Chiang L H,Russell E L,Braatz R D.Fault diagnosis in chemical processes using Fisher discriminant analysis, discriminant partial least squares,and principal component analysis[J].Chemometrics and Intelligent Laboratory System, 2000,50(2):243-252.

[7] 郑望.多变量过程统计监控[D].北京:北京化工大学, 2008.

[8] 王晓华.过程监控与故障诊断的ICA-MPCA方法[D].大连:大连理工大学,2008.

An Approach for Batch Process Fault Diagnosis Study Based on MFDA-PCA

GUAN Mingli,YUAN Zhonghu
(School of Information Engineering,Shenyang University,Shenyang 110044,China)

Aiming at the traditional MPCA methods’defects of online data integrity and real-time differential,an approach for batch process fault diagnosis based on MFDA-PCA is proposed,which is easy to study the online fault diagnosis during the batch processes.At first step,MFDA model is used for analyzing similarity by comparing the normal times of online batch data with that of historical batches; next,an optimal similarity PCA model in historical batch processes is built to analyze online batch data;and then,the task for online monitoring and fault diagnosis to the whole batch processes production has been completed.The effectiveness of the proposed method was verified by penicillin fermentation simulation.

MFDA;PCA;batch process;similarity analysis

TP 277

A

【责任编辑 杨 敏】

1008-9225(2010)02-0028-04

2009-12-15

关明礼(1981-),男,辽宁沈阳人,沈阳大学硕士研究生;原忠虎(1962-),男,辽宁大连人,沈阳大学教授,博士.