基于差分法的土石坝数值模拟研究

郝 哲,朱一飞,王铁男

(1.沈阳大学 建筑工程学院,辽宁 沈阳 110044; 2.东北大学 资源与土木工程学院,辽宁 沈阳 110004)

基于差分法的土石坝数值模拟研究

郝 哲1,朱一飞2,王铁男1

(1.沈阳大学 建筑工程学院,辽宁 沈阳 110044; 2.东北大学 资源与土木工程学院,辽宁 沈阳 110004)

对有限差分法的基本原理及分析过程进行了阐述,并对FLAC数值计算软件的功能、处理过程、应用范围以及与其他软件的比较等方面进行了系统论述.基于现场调研收集的相关坝体的资料,应用FLAC程序对阜新电厂四灰场主坝进行位移、变形、应力分析,以判断坝体结构的稳定状态.结果表明,该坝体在应力、位移、变形上是满足要求的,是稳定的,在长时间内不会出现问题.

阜新电厂;土石坝;差分法;FLAC;数值模拟

用当地土料和砂、砂砾、卵砾、石渣、石料等筑成坝,依靠坝体自身重量维持坝的稳定,是一种古老而至今还广泛使用的大坝形式,称为土石坝[1].《阜新发电厂四灰场主坝坝体稳定性监测研究》是沈阳大学承担的横向课题.课题组对电厂四灰场主坝进行现场调研,了解了大坝历经20多年后的运行现状,对其外型、边坡养护、水库水位、周围环境、边坡植被等情况进行了考察,并收集了坝体设计的相关数据资料、场地地质资料及物理力学参数指标等,作为本文分析的基础资料.

阜新电厂四灰场主坝位于阜新市北11 km处,是该电厂粉煤灰及废水的主要排泄场地[2].场区地面标高界于219.40～417.60 m之间,为低山丘陵区.整个大坝呈椭圆形,坝的南侧为一“U”形谷,谷底较平坦,宽约100 m.沟谷西侧为黄土陡崖,崖高6～8 m,近于直立.东侧为居民区,坝肩部分为岩石山坡,部分为土山坡,山坡坡度约为15°,山坡上植被较差.西侧坝肩为岩石山坡,山坡坡度约为12°.大坝北侧为一灰渣库.在主坝东北角处有一副坝,呈椭圆形,坝长约为50 m,坝宽约20 m.主坝坝体为均质土石坝,坝高35 m,坝长448.14 m,顶宽为5 m,底宽为45 m.坝基标高为224 m,坝体外侧有一层碎石护坡,厚度约为0.3 m;内侧部分为碎石护坡,部分为草皮护坡.坝内水位很低,水主要集中在北侧,南侧部分可见坝底.

1 计算程序

1.1 拉格朗日差分法

所谓差分法,是把基本方程和边界条件(一般均为微分方程)近似地改用差分方程(代数方程)来表示,把求解微分方程的问题改换成求解代数方程.

本文采用的计算方法为拉格朗日差分法,这是一种利用拖带坐标系分析大变形问题的数值方法.模型经过网络划分,物理网格映射成数学网格,数学网格上的某个结点就与物理网格上的相应结点坐标相对应.对某一个结点而言,在每一时刻它受到来自其周围区域的合力影响.如果合力不等于零,结点就具有了失稳力,就要产生运动,根据牛顿定律,结点就要产生加速度,进而可以在一个时步中求得速度和位移的增量.对每一个区域而言,可以根据其周围结点的运动速度求得它的应变率,然后根据材料的本构关系求得应力的增量.由应力增量求出 t和 t+Δt时刻各个结点的不平衡力和各个结点在 t+Δt时的变加速度.对加速度进行积分,即可得结点的新坐标值.由于物体的变形,单元发生局部的平均旋转或整旋,只要计算相应的应力改正值,通过应力叠加就可以得到新的应力值,到此计算为一个循环.然后按时步进行下一轮的计算,如此一直进行到问题收敛[3,4].

1.2 数值模拟软件选取

关于数值计算方法,目前较为常用的有:有限元法、边界元法、有限差分法、加权余量法、离散元法、刚体元法、不连续变形分析法、流形元法等.前四种方法是基于连续介质力学的方法,随后三种方法是基于非连续介质力学的方法,最后一种方法具有这两大类方法的共性.有限单元法是最常用的,但一般用有限元计算的位移通常较实测的结果要小,有时甚至差一两个数量级,究其原因,主要是在计算中忽略了非线性的大变形和沿弱面的不连续变形.有限差分法是将问题的基本方程和边界条件以简单、直观的差分形式来表达,专门求解岩土力学非线性大变形问题,能得到较满意的位移解,易于在实际工程中应用.

目前,面向各学科专业,针对不同的数值计算方法,已开发出众多的数值计算软件,其中有通用程序,也有专用程序.表1列出了目前国内外较知名的大、中型软件.

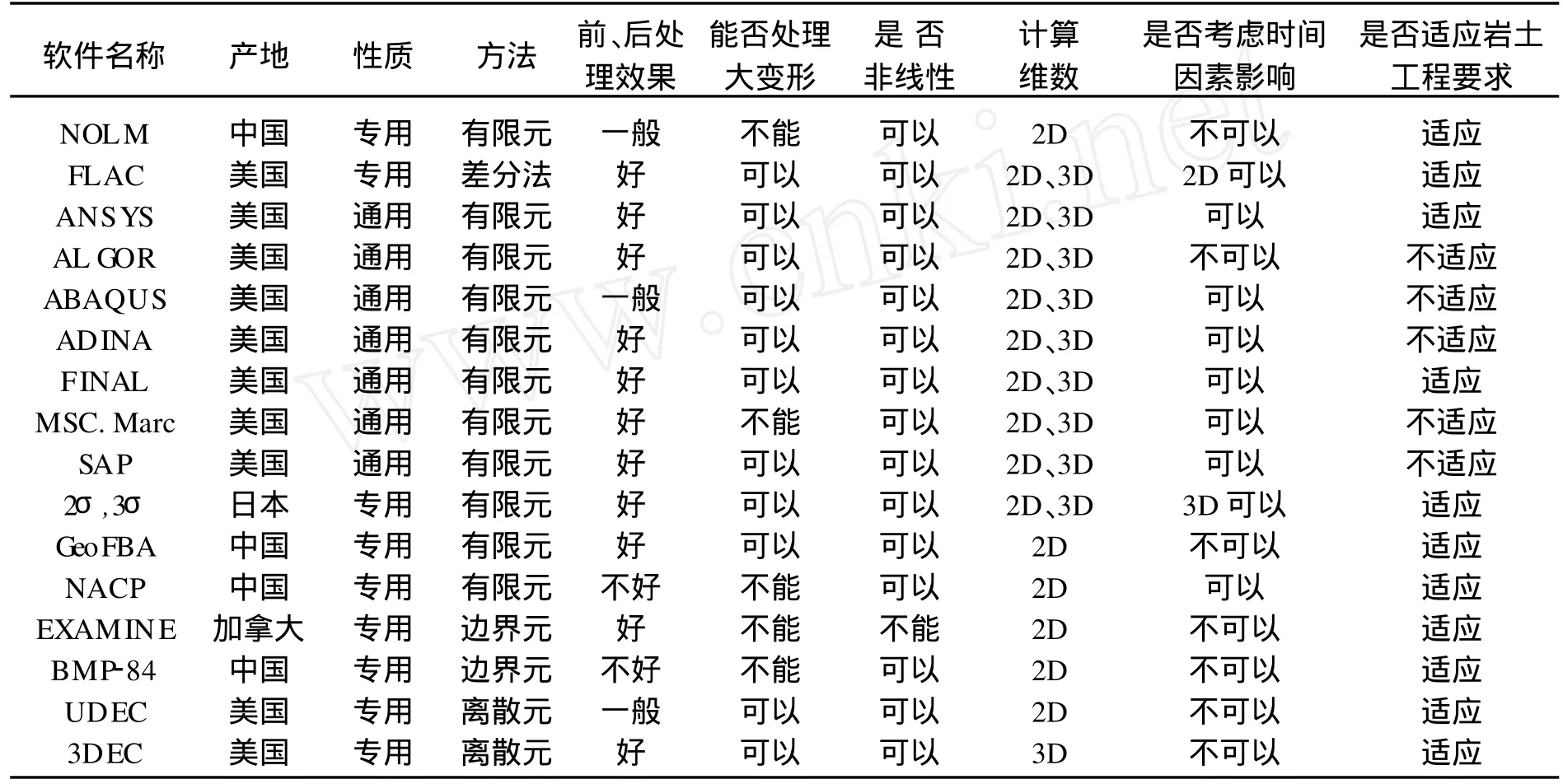
表1 各种数值计算软件功能对比

其中,FLAC程序(Fast Language Analysis of Continue)是基于拉格朗日差分法的国际知名大型数值计算软件,由美国 ITASCA Consulting Group.Inc.开发研制.主要应用于岩土力学分析,能对其应力、位移进行精确计算,它采用显式拉格朗日算法及混合离散单元划分技术,代替了原先广泛使用的隐式有限元法[5].能够精确地模拟材料的塑性流动和破坏,对静态系统模型也可采用动态方程来进行求解.因为不需要形成刚度矩阵,故占用微机内存小,便于求解大型工程问题.与有限元计算相比,FLAC解线性问题较慢,而解非线性问题较快,特别是在大变形和几何非线性的情况下,具有明显优势.FLAC程序具有计算灵活的特点,是其他有限元程序无法比拟的,特别是它通过类似批处理文件的前处理可以任意改变原始参数,同时还能保持前后计算的连续性.也就是说后面参数改变,可以继续在原基础上计算,而且这种变化十分方便.这样就为变弹模法模拟时间因素的影响创造了条件,而其他大多数有限元程序很难做到这一点.FLAC程序可以用于分析多种岩石材料、断层和节理,可以模拟不同加载条件下的地应力场生成、边坡或地下硐室开挖、大坝和地基的诱发破坏、混凝土衬砌、锚杆或锚索设置、地震工程和岩石爆破、地下渗流等.本文的数值计算采用FLAC 3.0程序.

2 阜新电厂四灰场主体坝体FLAC分析

2.1 计算模型

计算坝体结构时,为了使地基对结构应力的影响反映出来,必须把和结构相连的一部分地基取为弹性体,与结构一起作为计算对象.按照弹性力学中关于接触应力的理论,所取地基范围大小应视结构底部的宽度而定(与结构高度无关).早期文献[6,7]中,一般都建议在结构的两边和下方把地基范围取为大致等于结构底部宽度B.但后来一些文献[8]中,大都把所取的范围扩大为L= 2B,个别文献[9]还把它扩大为 L=4B.此外,还有一些文献[10]认为,应当把地基范围取为矩形区域,以便将铰支座改为连杆支座,减少对地基的人为约束.笔者认为在地基比较均匀而且结构与地基弹性相差不大的情况下,没有必要使 L超过2B,用铰支座比连杆支座更接近实际情况,地基范围的形状影响也不大.

对于阜新电厂主坝,由于为土坝,故其结构与地基结构相当,取 L=2B即可.为便于计算,取地基为矩形区域比较符合程序要求.得计算模型如图1所示.

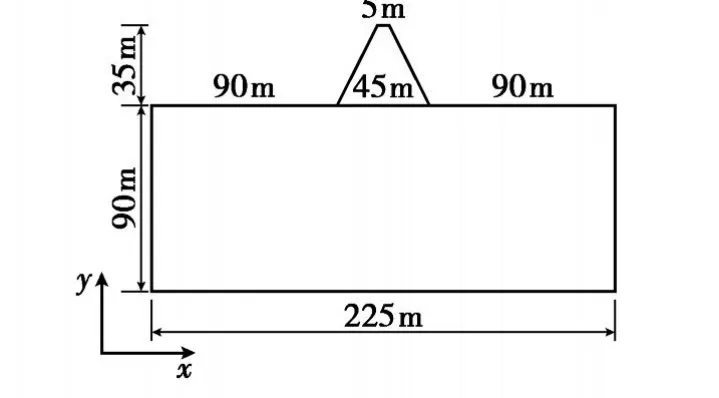
图1 坝体计算模型

FLAC软件在给定的区域或范围内可赋予的本构模型有:横观各向同性弹性模型(Anisotropic)、弹性本构模型(Elastic)、摩尔-库仑弹塑性模型(Mohr-Coulomb)、零模型(Null)、应变软化模型(SS)、彻体节理模型(Ubiquitous).由于土体有一定的流塑性,岩石也有一定的弹塑性,故选择摩尔-库仑弹塑性本构模型.

2.2 网格划分

根据程序要求,用相隔等间距 h且平行于坐标轴的两组平行线组成网格.划分横向网格数为225 m/5 m=45,纵向网格数为(90 m+35 m)/5 m =25,网格总个数为45×25=1 125.网格划分如图2所示,且坝体横截面的边缘轮廓均能由网格结点表示出来.

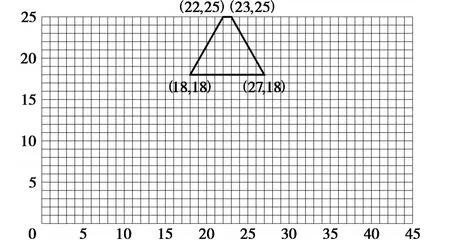
图2 网格划分

2.3 物理力学参数分析

根据阜新电厂四灰场地质勘测资料,按三层考虑:坝基土层厚度约为5.4 m;砂石层厚度为10.1 m;底层为花岗岩.各层物理力学参数如下:

(1)对于坝体本身.由勘测资料可知,筑坝材料为黄土.该土为黄～黄褐色,含少量碎石、角砾,稍湿,硬塑;最大干容重为1.80～1.81 g/cm3,最佳含水质量分数为15.4%～15.8%,可溶盐质量分数为0.03%,密度为1.4～1.61 g/cm3,内摩擦角为22.3°,弹性模量为104kPa.据此计算剪切模量S=3.79 MPa,体积模量 K=9.26 MPa,粘聚力COH=0.049 MPa.

故该层物理力学参数为:S=3.79 MPa,K= 9.26 MPa,DENS=1.47×10-3kg/cm3,FRIC= 22.3°,COH=4.9×10-2MPa.

(2)花岗岩层.根据勘测资料可知,主坝地段花岗岩实验结果如下:吸水率 0.73%,容重2.56 g/cm3,比重 2.62 g/cm3,风干抗压强度69.20 MPa,软化系数0.91,内摩擦角37°,泊松比0.384.故弹性模量 E=1.774×107kPa.剪切模量 S=6.4×103MPa,体积模量 K=2.54×104MPa,粘聚力COH=21 MPa.

故该层物理力学参数为:S=6.4×103MPa, K =2.54 ×104MPa,DENS = 2.56 × 10-3kg/cm3,FRIC=37°,COH=21 MPa.

(3)地基土石层.由于该层是由土层和砂石层组成,且每层厚度较小,在程序中不能一一表示出来,所以由土层和砂石层的各项力学参数取其平均值可得出结果.土层参数可与筑坝黄土相仿,砂石层力学参数可根据相关资料查得.密度取2.0 g/cm3,摩擦角取30°.剪切模量 K=5.7 ×102MPa,体积模量 K=5.6×102MPa,粘聚力取COH=10 MPa.

故该层物理力学参数为:S=5.7×102MPa, K=5.6×102MPa,DENS=2.0×10-3kg/cm3, FRIC=30°,COH=10 MPa.

2.4 边界条件及外部载荷的加入

由计算模型可知,由于所选计算区域的边界所受扰动已经很小,甚至可以忽略不计,故其边界可以看做为被固定的刚性边界(即没有变形,也没有位移),对于坝顶边界来说是没有约束的.

由《施工图阶段工程、水文地质勘察任务书》可知,发展远景坝顶标高为276 m,发展远景最高水位标高为271 m,故最高水位离坝顶5 m.水深h为30 m,则水对坝体底部侧压应力为

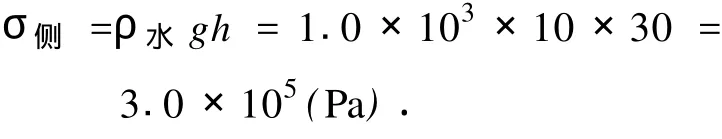
式中,σ水为水的密度,kg/m3;g为重力加速度, m/s-2.

由勘测资料可知,地下水位为2 m,即在坝体有水侧面的水深为30 m,坝基15 m为土砂层和水层,15 m以下为花岗岩层.对于坝体无水侧面,坝基15 m为土砂层,地下水高为13 m,15 m以下为花岗岩层,该坝体左侧为有水侧面.则对于网格(0,0)点处的应力为

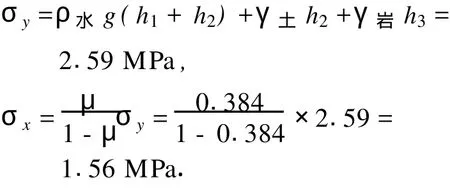
同理,网格(0,15)点处的应力为

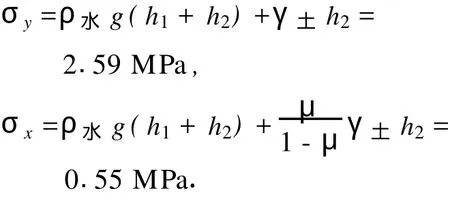
网格(0,18)点处的应力为:

σx=σy=1.0×103×10×30=0.3 MPa.式中,h1为土坝中水头高度(m),h2为地基土石层中水头高度(m),h3为花岗岩层中水头高度(m),μ为泊松比,γ为重度(N/m3).

对于坝体无水侧面,由于地下水位为2 m,在程序中较小,无法表示出来,可认为从地基土层到顶部应力为均匀变化的.则对于网格处(45,0)点处的应力为

对于网格(45,15)点处的应力为

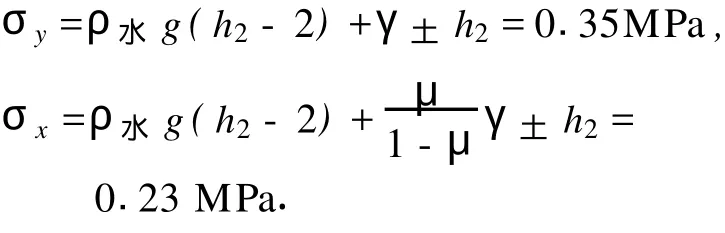
网格(45,18)点处的应力为

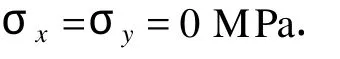
2.5 计算结果分析

将坝体及坝基各层材料的物理力学参数、边界条件和外部荷载按照FLAC程序所需格式组成数据文件,输入程序运算.

2.5.1 应力分析

对于所取计算模型的主应力矢量、水平方向应力的等值线、竖直方向应力的等值线,由程序计算可得结果如图3～图5所示.从图中可知,主应力变化是比较均匀的.对于整个模型来说,最大主应力在模型底层,主要是由各层材料的自重力产生.而对于坝体应力从上往下变化几乎是线性的,其最大主应力也在坝体底部.从图4、图5可知,坝体对其周围的应力影响在竖直方向较大,水平方向较小,水平方向的影响主要集中在土砂层.计算结果的最大主应力为2.814 MPa,在允许范围内.

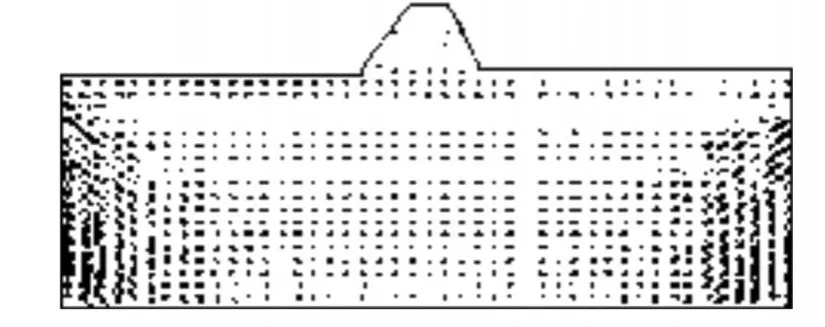
图3 主应力矢量(ST)

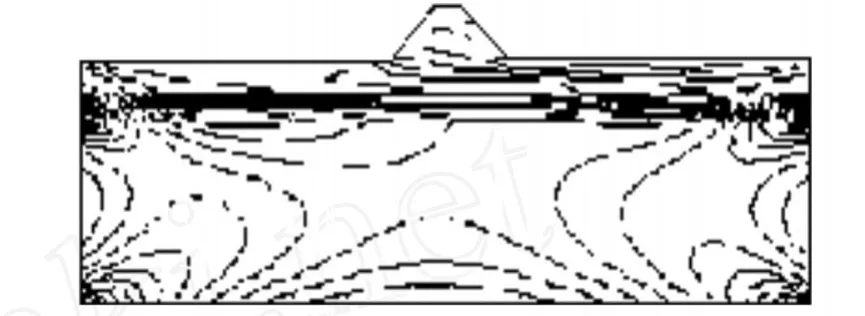
图4 水平方向应力等值线(SXX)

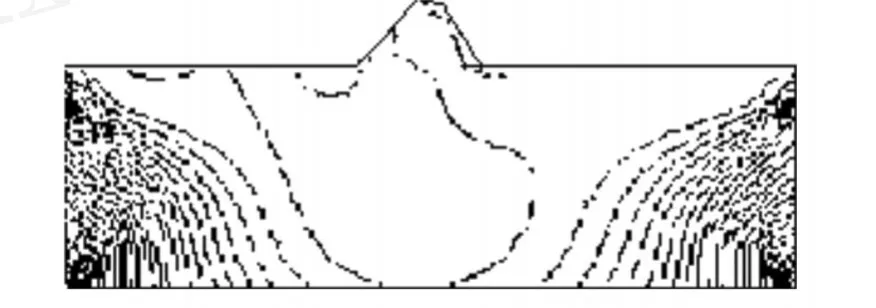
图5 竖直方向应力等值线(SYY)

2.5.2 位移分析

对于所取计算模型的位移矢量、水平方向位移等值线、竖直方向位移等值线,由程序计算可得结果如图6～图8.

图6 位移矢量(D)

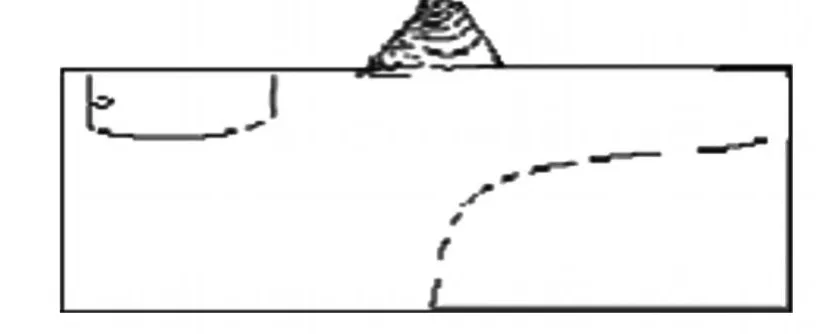
图7 水平方向位移等值线(XD)

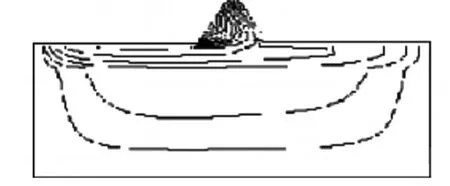
图8 竖直方向位移等值线(YD)

从图中可知,对于整个模型总位移主要集中在坝体,坝基的位移由上往下越来越小.对于水平方向的位移也是主要集中在坝体,而坝基几乎没有.竖直方向上的位移在坝体上尤为突出:一是由于水压力的竖向分力,二是由于坝体的自重.坝基有一部分沉降,也是由于自重和水压力.

当程序计算到800步时位移值已经收敛,该点的位移值为3.093 cm,在允许范围内(设计水平位移在总宽度的0.5%以内,45 m×0.5%= 22.5 cm).坝体计算的最大水平位移为3.25 cm,最大竖直位移为2.25 cm,在允许范围内(设计最大沉降为总高度的1%以内,35 m×1%=35 cm).而对于整个坝体的最大位移为3.359 cm,也在允许范围内.

3 结 论

本文基于差分法对阜新电厂四灰场主坝进行了数值模拟研究.通过对其进行实地整理分析,提炼出所需物理力学参数及荷载作用参数.根据坝体实际情况,在FLAC程序计算中选择摩尔—库仑弹塑性本构模型,并且选择扩展基础为矩形,有利于网格的划分.通过应用FLAC程序所作的数值分析可以得出,该坝体在应力、位移方面是满足要求的,是稳定的.由于边坡有一层护石,还有草皮护坡都可以增加坝体的稳定性,在计算中比较保守,而且现在坝内水位很低,个别地方坝体甚至接触不到水,按照最高设计水位计算,坝体是稳定的,长时间内不会出现问题.对于坝体的渗流方面,由于需要长期监测(3～5年,甚至10多年),本文没有涉及到,但它是坝体监测的一个重要组成部分.该坝由于水位低、水少,所以渗流方面也是符合规定的.

[1] 白永年,吴士宁,王洪恩.土石坝加固[M].北京:水利电力出版社,1992:2-3.

[2] 北京有色冶金设计研究院.阜新电厂灰渣库设施施工图、阶段工程水文地质勘测任务书[R].1983:20-26.

[3] 张东日,陶连金,李风仪,等.拉格朗日元法及其应用软件FLAC[J].矿山压力与顶板管理,1997,14(3):224-226.

[4] 杨立强,张中杰,林舸,等.FLAC基本原理及其在地学中的应用[J].地学前缘,2003,10(1):24.

[5] 龚纪文,崔建军,席先武,等.FLAC数值模拟软件及其在地学中的应用[J].大地构造与成矿学,2002,26(3):321 -325.

[6] 阎中华.土石坝稳定计算方法评述[J].人民黄河,1995, 17(7):33-37.

[7] 吴中如,顾冲时,沈振中,等.大坝安全综合分析和评价的理论、方法及其应用[J].水利水电科技进展,1998,18 (3):2-6,65.

[8] 傅琼华,黄真.土石坝安全监测及其资料整理分析方法综述[J].江西水利科技,1997,23(2):124-128.

[9] 方卫华.综论土石坝的安全监测[J].红水河,2002,21 (4):64-67.

[10] 方朝阳,夏富洲.土石坝安全监测综合评判准则研究[J].武汉大学学报,2001,34(5):27-31.

Numerical Simulation Study on Earth-Rock Dam Based on Calculus of Difference

HAO Zhe1,ZHU Yifei2,WAN G Tienan1
(1.School of Architectural and Civil Engineering,Shenyang University,Shenyang 110044,China;2.College of Resources and Civil Engineering,Northeastern University,Shenyang 110004,China)

The basic theory and analytic procedure about the calculus of difference are elaborated.The function,disposed process,used realm ofFLAC and comparison to other software are introduced systematically.Based on information collected from Fuxin Electric Power Plant,FLAC was used to calculate the displacement,deformation and stress of the dam to determine the stability of the dam.The results show that the dam can meet the requirements at the aspects of stress,displacement,and it is stable in a long time without problems.

fuxin electric power plant;earth-rock dam;calculus of differences;FLAC;numerical simulation

TV 698.1

A

【责任编辑 杨 敏】

1008-9225(2010)02-0023-05

2009-03-22

郝 哲(1972-),男,辽宁沈阳人,沈阳大学教授,博士后研究人员.