一类训练前馈神经网络的梯度算法及收敛性
邵红梅,安凤仙
(1.中国石油大学数学与计算科学学院,山东东营 257061;2.淮阴工学院数理学院,江苏淮安 223003)
一类训练前馈神经网络的梯度算法及收敛性
邵红梅1,安凤仙2
(1.中国石油大学数学与计算科学学院,山东东营 257061;2.淮阴工学院数理学院,江苏淮安 223003)
为加速网络训练,给出学习率的一种更广泛的选取方式,并从理论上证明这类新的变学习率的梯度学习算法的收敛性和训练过程中误差函数的单调递减性。
前馈神经网络;收敛性;变学习率;梯度算法
梯度法是训练神经网络的一种简单又常用的学习算法[1-6]。在梯度算法中,学习率的大小对网络误差函数的收敛性和收敛速度有很大的影响[5,7-8]。对于一般的优化问题,为了保证目标函数的下降和算法的收敛,线搜索是确定学习步长的常用方法,如精确一维搜索以及按 Ar mijo-Goldstein准则、Wolfe-Powell准则等进行确定步长的非精确线搜索[9,10]等,但是在实际应用中它们往往需要花费很大的计算量或很多次繁琐的试探性工作。为此,针对神经网络训练,人们提出了很多选取学习率的改进策略[1-2,7-8,11-12]。受文献 [1]的启发,笔者给出一种更广泛的简单选取学习率的规则,并以训练一个两层的前馈神经网络为例,严格证明对应的批处理梯度算法的收敛性。
1 变学习率的梯度学习算法
为了方便叙述和简化证明过程,考虑具有N个输入单元和 1个输出单元的两层前馈神经网络。记W =(w1,w2,…,wN)为整个网络的连接权构成的权向量,记σ(·)为输出单元对应的激活函数 (常用Sigmoid类型的函数[2,5])。给定一组训练样本集{ξi,Oi,当全部呈现给网络后,得到如下误差函数:

其中

对应的梯度函数为
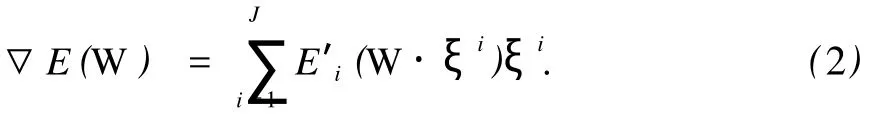
任给初始权值W0∈RN,每完成一个训练周期后,按如下规则不断进行更新:

其中,ηn>0为第 n个训练周期内的学习率,且从某给定初值η0>0开始,ηn随训练周期的增加而按下述规则变化:
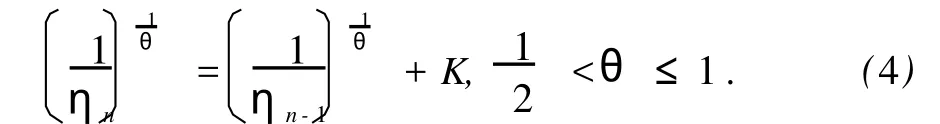
式中,参数 K>0是一个预先取定的常数。针对不同问题,K>0的取值可能不同,但这不影响算法的收敛性能。

在证明学习率按公式(4)变化的这类批处理梯度算法(3)的收敛性之前,需要作如下假设:
假设2 权序列{Wn}一致有界,即存在有界闭区域Φ满足{Wn}⊆Φ;
假设3 误差函数的稳定点集Φ0={W∈Φ:▽E(W)=0}为有限集。
2 几个重要引理
为了叙述方便,记ΔWn=Wn+1-Wn。
引理 1 设学习率(ηn)如公式 (4)所定义,则存在适当大的正常数γ>0和λ >K-θ,使
(1)ηn=O(n-θ);
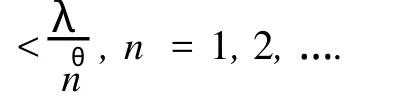

从而ηn=O(n-θ)得证。接下来,再利用同阶无穷小的定义,便可证得结论(2)和(3)。
引理3 设 F:Ω⊂Rn→Rm(n,m≥1)在有界闭集Ω⊂Rn上连续,集合Ω0={x∈Ω:F(x)=0}是有限点集。若序列 (xk)⊂Ω满足
引理 2是一个无穷项级数收敛定理,其证明可仿照文献[1]中的引理 3.5给出。
引理 3是证明强收敛结论的一个有力工具,其证明与文献[9]中定理 3.5.10相似。
引理 4 误差函数 E(W)如式 (1)所定义且假设 1成立,那么对任意的初值W0∈RN,由算法(3)得到的误差函数序列{E(Wn)}是单调递减的,即

其中N0∈N为某个自然数。
防治措施:①强化药剂防治,从5月份开始,每隔15天交替喷施波尔多液和杀菌剂,保证每次阴雨天气环境中,枝条和叶片都有药剂的保护。喷药应细致全面,枝干和叶片正反面都要均匀用药,防止遗漏。主要使用的药剂有5波美度石硫合剂、25%优库和50%多菌灵、70%代森锰锌800倍液和25%咪酰胺乳油3 000倍液。②增强树体抵抗力。合理施用有机肥,加强树体管理提高树体对病害的抵抗能力。③冬季修剪和生长季修剪结合,改善通风透光条件,合理负载,防止病菌滋生。④保持果园清洁,减少病菌传播。

对每个 Ei(t)在点Wn·ξi处作泰勒展开,得

其中Wn,i·ξi位于Wn+1·ξi和Wn·ξi的连线之间。
再由式 (1),(3),(5)和 (6)得

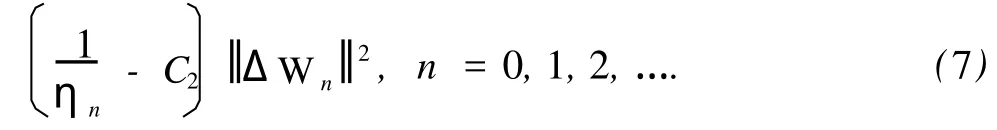

结合式 (7)和(8),有 E(Wn+1)≤E(Wn),n≥N0,即误差函数的单调性得证。
3 两个收敛性定理
定理 1(弱收敛定理) 设网络误差函数E(W)如式(1)所定义。从任意初始值W0∈RN开始,权序列{Wn}依据算法 (3)不断更新,并且随着训练周期的增加学习率按公式 (4)不断变化,那么在假设 1成立的情况下,可以得到如下结论:
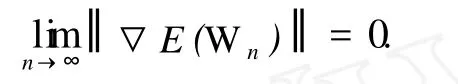
证明 一方面,由式(7)可得

注意到 E(Wn)≥0对所有的 n=0,1,2,…均成立,因此在上式中令 n→∞,便有
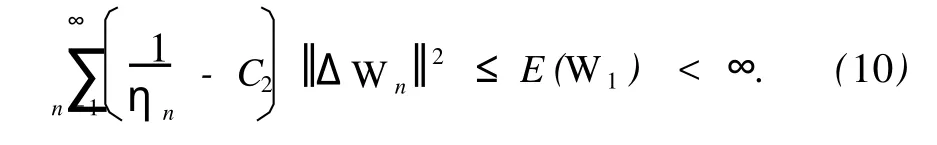

故
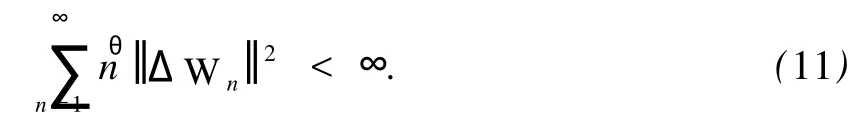
再结合式(3)和引理 1(2),便可验证下式成立:
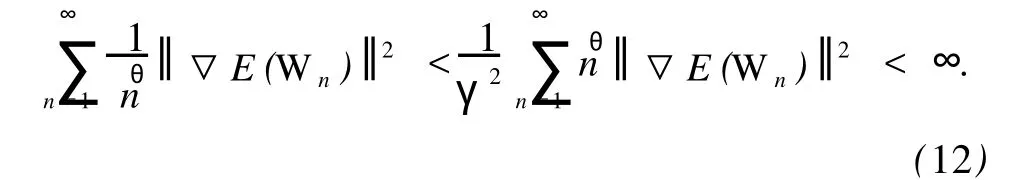
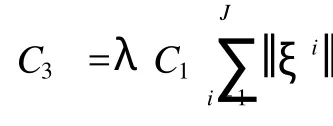

因此,应用中值定理并结合E″i(t)函数的有界性,便可做出如下估计:

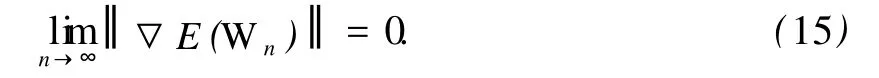
即弱收敛得证。
定理 2(强收敛定理) 在定理 1的基础上,若假设 2和假设 3也成立,那么对任意的初值W0∈RN,由算法 (3)得到的权序列{Wn}是强收敛的,即存在W*∈Φ0满足

证明 由假设1知,梯度函数▽E(W)在RN上连续。另外,由式 (13)和弱收敛结论可验证以下两个等式成立:

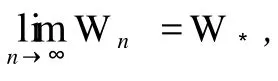
[1] WU W,FENG G R,L I X.Training multilayer perceptrons via minimization of sum of ridge functions[J].Advances in Computational Mathematics,2002,17:331-347.
[2] 吴微.神经网络计算 [M].北京:高等教育出版社, 2003:6-10.
[3] HAGAN M T,DEMUTH H B,BEALEM.神经网络设计[M].戴葵,宋辉,谭明峰,等,译.北京:机械工业出版社,2003.
[4] 蔡吉刚,李树荣,王平.基于小波神经网络的自适应控制器设计 [J].中国石油大学学报:自然科学版, 2007,31(5):141-143.
CA IJi-gang,L I Shu-rong,WANG Ping.Design of adaptive controller based on wavelet neural network[J].Journal of China University of Petroleum(Natural Science E-dition),2007,31(5):141-143.
[5] RUMELHARTD E,MCCLELLAND J L,PDP Research Group.Parallel distributed processing-explorations in the microstructure of cognition[M].Cambridge:M IT Press, 1986:320-340.
[6] SHAO H M,WU W,L I F.Convergence of online gradientmethod with a penalty ter m for feedforward neural networkswith stochastic inputs[J].NumericalMathematics, A Journal of Chinese Universities(English Series),2005, 14(1):87-96.
[7] JACOBS R A. Increased rates of convergence through learning rate adaptation[J].Neural Networks,1988,1 (4):295-307.
[8] MAGOULAS G D.Effective neural network training with a different learning rate for each weight:The 6th IEEE International Conference on Electronics,Circuits and Systems,Pafos,Cyprus,5-8 September,1999[C].Cyprus:IEEE,c1999:591-594.
[9] 袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学教育出版社,2001.
[10] ARM I JO L.Minimization of function having Lipschitz continuouse first partial derivatives[J].Pacific Journal ofMathematics,1966,16(1):1-3.
[11] CHAN L W,FALLSI DE F.An adaptive training algorithm for back-propagation networks[J]. Computer Speech and Language,1987(2):205-218.
[12] LUO Z.On the Convergence of the LMS algorithm with adaptive learning rate for linear feedforward network[J]. Neural Computation,1991,3(2):226-245.
(编辑 修荣荣)
A class of gradient algorithm s with variable learn ing rates and convergence analysis for feedforward neural networks tra in ing
SHAO Hong-mei1,AN Feng-xian2
(1.School of M athem atics and Computational Science in China University of Petroleum,Dongying257061,China; 2.Departm ent of Com puter Science,Huaiyin Institute of Technology,Huaian223003,China)
A general updating rule for learning rateswas presented and the convergence of the corresponding batch gradient algorithmswith variable learning rates for training feedforward neural net works was proved.The monotonicity of the error function in the training iteration was also proved.
feedforward neural networks;convergence;variable learning rate;gradient algorithm
TP 183
A
10.3969/j.issn.1673-5005.2010.04.035
1673-5005(2010)04-0176-03
2009-12-16
中国石油大学博士科研基金(Y080809)
邵红梅(1981-),女(汉族),山东曹县人,讲师,博士研究生,从事神经网络计算及数据挖掘方面的研究。

