具有终端收敛能力的 Stewart平台饱和 PD控制
赵东亚,邹 涛,王治平,何熊熊
(1.中国石油大学机电工程学院,山东东营 257061;2.浙江工业大学信息工程学院,浙江杭州 310023; 3.中石化洛阳分公司,河南洛阳 471000)
具有终端收敛能力的 Stewart平台饱和 PD控制
赵东亚1,邹 涛2,王治平3,何熊熊2
(1.中国石油大学机电工程学院,山东东营 257061;2.浙江工业大学信息工程学院,浙江杭州 310023; 3.中石化洛阳分公司,河南洛阳 471000)
用跟踪误差小数幂技术,研究一种新的具有终端收敛能力的 Stewart平台饱和 PD加重力补偿控制方法,运用LaShalle´s不变集原理分析系统稳定性,通过数值仿真验证新方法的有效性。结果表明,新方法能够保证系统在控制器输出存在饱和的情况下全局渐近稳定,且比传统的饱和 PD加重力补偿控制方法具有更快的收敛速度。
饱和控制;PD控制;机器人;控制;Stewart平台;并联机器人;数值方法
Stewart平台是一种典型的并联机构,能够实现空间中的六自由度运动,具有刚度大、承载能力强、精度高、结构紧凑、加速度快等优点,因此在生产实践中有着广泛应用[1-3]。工业中多选用电机或液压缸作为 Stewart平台的执行器,受物理限制,电机和液压缸都不能输出无限大力矩,因此控制器到执行器之间会出现饱和问题。如果不考虑控制器输出饱和,会影响系统稳定性,甚至会出现执行器过热、损坏机械设备等问题[4-5]。目前为 Stewart平台设计的控制器大多未考虑输出饱和问题,因此在应用于工业实践时必须谨慎地选择初始条件,以免损坏机电设备。PD加重力补偿控制方法是 Stewart平台常用的控制手段,在工业中有着广泛应用。Zavala Río A等[6]为串联机器人提出了一种饱和 PD加重力补偿控制方法,该方法能够实现系统全局渐近稳定,但由于在控制器设计中使用了饱和函数,从而导致系统响应时间变得缓慢,并且由于串联机器人动力学模型与并联机构存在很大差异,该方法不能直接应用于 Stewart平台。针对这一问题,笔者根据 Stewart平台动力学特点,运用跟踪误差小数幂技术[7]和LaShalle´s不变集原理,提出一种新的具有终端收敛能力的 Stewart平台饱和 PD加重力补偿控制方法,并分析系统稳定性,最后通过数值仿真研究,验证本文方法的有效性。
1 Stewart平台动力学模型
六自由度 Stewart平台在任务空间中执行生产任务,现有文献中大都使用 Euler-Lagrange方法建立任务空间动力学模型[1-3],表达式为

式中,P∈R6代表上平台中心在基准坐标系中的位姿;M(P)∈R6×6为正定对称惯性矩阵;C(P,˙P)˙P∈R6代表哥氏力和向心力向量;G(P)∈R6代表重力向量;J∈R6×6代表 Jacobian矩阵;f∈R6代表各滑移关节输出力矩。
动力学方程(1)具有如下性质[1-3]。

性质 2 存在正常数 m和 ¯m使不等式 m I≤M(P)≤成立;
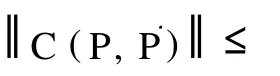
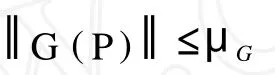


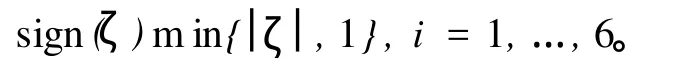
2 饱和 PD控制器设计
为设计饱和控制器,定义如下饱和函数[6]:
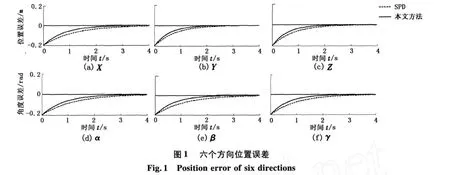
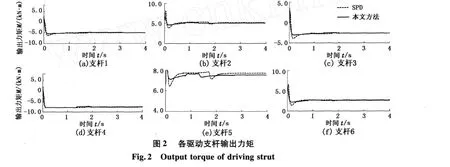
定义 1 给定正常数L和M并且L ①对于所有ζ≠0,ζ σ(ζ)>0; 本文研究 Stewart平台设定值控制问题,跟踪误差定义为式中,ΔP∈R6为跟踪误差。 串联机器人设计的饱和 PD加重力补偿控制器[6]为 其中 式中,KP,KD为正定对角矩阵,分别代表比例控制增益矩阵和微分控制增益矩阵;σi(·)为定义1中的严格递增线性饱和函数,且满足如下条件: γi代表重力向量第 i个分量绝对值的上界。条件γi≤Li≤Mi≤Ti是为了保证控制器能够提供足够大的力矩,以使系统在运动过程中除克服重力影响外可以提供足够的 PD控制以使系统稳定。 由于控制器(4)中没有考虑 Jacobian矩阵,因此不能直接应用于 Stewart平台任务空间控制。该控制器中使用了饱和函数,使得系统闭环响应速度比未考虑控制器饱和的控制方法要慢[9]。 设计控制器前作如下假设: (1)六自由度 Stewart平台上平台质心在任务空间中的位置 P和速度 ˙P可测; (2)六自由度 Stewart平台上平台在任务空间中的期望值向量 Pd∈R6为有界常数向量; (4)系统重力向量所有分量Gi(P)绝对值的上界 gi满足不等式 (可参考性质4),gi≤Li≤Mi≤F, i=1,…,6。 假设(3)是合理的,因为在轨迹规划和机构设计中可以避免Jacobian奇异问题,因而能够保证 J-1存在且有界。 针对 Stewart平台特点,运用位置误差小数幂技术设计饱和 PD加重力补偿控制器,表达式为 其中 式中,KP1,KP2分别为线性和非线性比例控制增益矩阵;KD为微分控制增益矩阵。 对于向量 x∈Rn,s=[σ(x1),…,σ(xn)]T,σ为对于正实数L和M的严格递增线性饱和函数,并且满足如下不等式: 比较文献[6]控制器 (4)和本文控制器 (5),可以看到本文控制器多了 J-1和 -KP2sig(ΔP)α项。其中J-1是针对 Stewart平台在任务空间中设计控制器而引入的。位置误差小数幂具有终端收敛能力,因此 -KP2sig(ΔP)α可以保证系统具有更快的收敛速度和更高的跟踪精度。当取 J-1=I(I∈Rn×n为单位矩阵)时,本文控制器可以应用于串联刚性机器人。如果在 J-1=I的条件下,取α =1, KP1+KP2=KP,则本文控制器 (5)等同于文献[6]控制器 (4),因此控制器 (4)是本文控制器 (5)的一种特殊情况。 将控制器(5)代入系统动力学方程(1)可得 本文中 0n∈Rn指 n维欧氏空间的原点。 定义如下Lyapunov函数: 其中 由定义 1中的 ①和性质 2可知Lyapunov函数V(ΔP,˙P)是正定的。由饱和函数的单调性以及性质2可知 Lyapunov函数 V(ΔP,˙P)径向无界。 将Lyapunov函数(8)沿闭环系统(7)对时间 t求导数并且考虑性质 5可得: 表 1为控制器参数。 表1 控制器参数Table 1 Parameters of controller 为验证本文提出的具有终端收敛能力的 PD加重力补偿控制算法的有效性,使用MathWorks公司提供的 SimMechanics六自由度 Stewart Platform仿真平台作为被控对象进行仿真研究。 仿真中对文献[6]提出的控制器 SPD(即控制器 (4)中的参数α=1,KP=Kp1+KP2)和本文方法式(5)进行比较,以进一步说明本文方法的有效性。假设各驱动支杆能够输出的最大力矩为 8 500 N,期望值为 图1为任务空间跟踪误差。图1表明本文方法具有终端收敛能力,具有更快的收敛速度和更高的控制精度。图 2为各驱动支杆输出力矩。从图 2中可以看出,两种控制方法具有相似的输出力矩,支杆 2和支杆5的输出力矩出现了饱和,但没有超过8.5 kN· m,仿真研究证明了本文控制方法的有效性。 由于 Stewart平台选用电机或液压缸作为执行机构,这些执行机构不能输出无限大力矩,因此从控制器到执行器之间存在饱和问题。传统饱和 PD加重力补偿控制中使用了饱和函数,因此导致系统输出响应缓慢。本文中针对 Stewart平台动力学特点,运用跟踪误差小数幂技术和 LaShalle´s不变集原理提出了一种新的具有终端收敛能力的饱和 PD加重力补偿控制方法,能够实现全局渐近稳定。与传统方法相比,本文方法具有更快的收敛速度。通过稳定性分析和数值仿真证明了本文方法的有效性。 [1] MERLET J-P.Parallel robots[M].Netherlands:Kluwer Academic Publishers,2000. [2] 孟浩龙,李著信,王菊芬,等.管内检测机器人在水平直管内运动的数值研究[J].中国石油大学学报:自然科学版,2007,31(3):103-108. MENG Hao-long,L I Zhu-xin,WANG Ju-fen,et al.Numerical study on movement of in-pipe inspection robot in horizontal straight pipeline[J].Journal of China University of Petroleum(Edition of Natural Science),2007,31 (3):103-108. [3] 徐东光,董彦良,吴盛林,等.液压驱动 Stewart平台非线性自适应控制器设计[J].机械工程学报,2007, 43(3):223-227. XU Dong-guang,DONG Yan-liang,WU Sheng-lin,et al. Nonlinear adaptive controller design for the Stewart platform by hydraulic driven[J].Chinese Journal of Mechanical Engineering,2007,43(3):223-227. [4] AGU I NAGA Ruiz E,ZAVALA Rio A,SANTI BANEZV, et al.Global trajectory tracking through static feedback for robot manipulators with bounded inputs[J]. IEEE Transactions on Control Systems Technology,2009,17 (4):934-944. [5] PENGW,L IN Z,SU J.Computed torque control-based composite nonlinear feedback controller for robotmanipulatorswith bounded torques[J].IET Control Theory and Applications,2009,3(6):701-711. [6] ZAVALA Río A,SANTI BBÁÑEZ V.Simple extensions of the PD-with-gravity-compensation control law for robot manipulators with bounded inputs[J]. IEEE Transactions on Control Systems Technology,2006,14(5):958-965. [7] AB I D I K,XU J-X,SHE J-H.A discrete-time terminal sliding-mode control approach applied to a motion control problem[J]. IEEE Transactions on Industrial Electronics,2009,56(9):3619-3627. [8] DAVL I AKOS I,PAPADOPOULOS E.Model-based control of a 6-dof edectrohydraulic Stewart-gough platform [J].Mechanism and Machine Theory,2008,43(11): 1385-1400. [9] ZAVALA RÍo A,SANTI BBÁÑEZV.A natural saturating extension ofthe PD-with-desired-gravity-compensation control law for robot manipulators with bounded inputs [J].IEEE Transactions on Robotics,2007,23(2):386-391. [10] KHAL I L H K.Nonlinear systems[M].3rd.New Jersey:Prentice-Hall,2002. (编辑 沈玉英) Saturating PD control approach with term inal convergence capability for Stewart platform ZHAO Dong-ya1,ZOU Tao2,WANG Zhi-ping3,HE Xiong-xiong2 A new saturating PD plus gravity compensation control approach with terminal convergence capability for Stewart platform was presented using decimal fraction power of tracking error.In light ofLaShalle´s invariance principle,the system stabilitywas analyzed.The effectivenessof the approachwas demonstrated by numerical simulation.The results show that the method can achieve asymptotic stability in the presence of controller output saturation.The proposed approach has faster convergence speed than conventional saturating PD plus gravity compensation control algorithm. saturating control;PD control;robot;control;Stewart platform;parallel robot;numericalmethods TP 242.2 A 10.3969/j.issn.1673-5005.2010.04.026 1673-5005(2010)04-0131-05 2009-12-15 国家自然科学基金项目(60604017);国家“863”高新技术研究项目(2009AA04z138);中央高校基本科研业务费专项资金资助(09CX04057A) 赵东亚(1975-),男(汉族),山东济宁人,讲师,博士,主要从事机械系统控制、非线性系统控制。
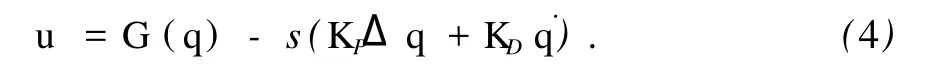
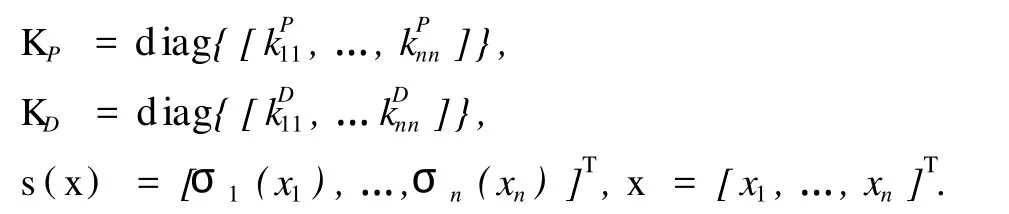
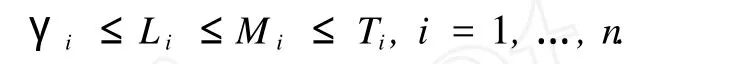



3 稳定性分析
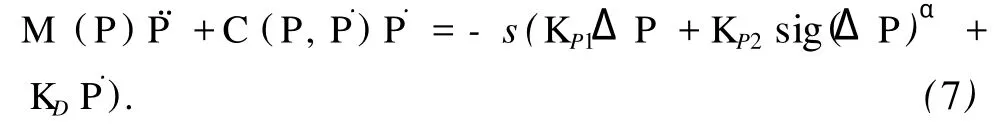



4 仿真验证


5 结束语
(1.College of Electromechanical Engineering in China University of Petroleum,Dongying257061,China; 2.College of Info rmation Engineering,Zhejiang University of Technology,Hangzhou310023,China; 3.SINOPEC Luoyang B ranch,Luoyang471000,China)

