应用齐次马氏域变对上海股市异常收益率的实证检验

武金存，封文丽，张跃辉

应用齐次马氏域变对上海股市异常收益率的实证检验

武金存，封文丽，张跃辉

（河北经贸大学金融学院，河北 石家庄 050061）

通过在收益率结构中使用齐次马氏域变模型研究异常收益率，描述以1996年10月到2010年2月的上证指数为研究对象的非线性动态异常收益率演进过程，并利用Johansen协整检验方法剔除其理性价值（即正常收益率），进而基于齐次马氏域变模型针对协整残差（即异常收益率）进行建模，用极大似然法拟合估计总体参数。最后根据实证结果，指出股市的宏观经济政策因素是影响我国股市异常收益率现象的主要原因，并提出相应的政策建议。

异常收益率；Johansen协整检验；齐次马氏域变模型

0 引言

异常收益率是实际收益率与正常收益率之差。能否获得异常收益率是验证金融市场有效性的方法之一。在长期异常收益率的度量中，重点是如何测度正常收益率。但目前仍没有可靠的实证结论支持资产定价模型，所以国内外对长期异常收益率度量的研究一直存在争议。本文采用学术界一贯的研究方法，将长期异常收益率的度量分为两类。一类为横截面研究法（事件时间研究法），即累计异常收益率（Cumulative Abnormal Returns，CAR）和购买并持有异常收益率（Buying and Holding Abnormal Returns，BHAR）；另一类为时间序列研究法（日历时间研究法），基本研究思路是：通过计算在一段时间内股票组合的平均收益(基于日历时间)并与基准收益进行对比。一般方法是先把每个日历月的平均收益通过Fama-French或CAPM模型进行回归，之后把考察横截距项（Intercept）显著与否作为判断弱于还是强于基准收益的标准。两种研究方法的不同之处是，前者不论月份之间事件发生频度和其他差异而赋予月份等权，后者不论事件发生的时间而将事件赋予等权。

然而时间序列研究法的常用方法不能连续动态地模拟异常收益率的变化。本质上，具有此类特征的序列，其生成过程是非线性的。AR(p)以及ARMA(p，q)和标准协整模型在样本期内假定分析对象有不变的均值、方差和持续性，不足以刻画股市收益内生的结构变化而产生的非线性特征。1982年，Engle提出ARCH模型描述收益波动随收益率水平变化的非线性行为，但尽管经过不断的完善，都没有改变均值方程是线性这个性质，因此其本质上仍是线性模型[1。 ]

由于以上的不足，本文提出用改进的Hamilton（1989）的马尔可夫时域转换模型研究异常收益率。经济时间序列所处状态的变化会引起相应参数的变化，并且状态之间的变化服从不可观测的离散时间，被称为“时域转换（regime switch）”。对于正常的经济力量和非正常事件导致的收益率变动，通过马尔可夫域变模型均可得到反映。中国股市正处于不断深化的成长期，选用该模型是比较合适的。本文基于一个改进的马氏域变模型，描述以上证指数为研究对象的非线性动态的异常收益率演进过程，在单位根检验和Johansen协整检验方法的基础上，用协整将正常收益率剔除，进而针对协整残差建模，并根据理论模型引入对收益率具有决定性影响的宏观经济变量，对我国股票市场是否存在异常收益率现象进行实证研究，并分析促使我国股票市场异常收益率发生变化的原因。

1 理论模型

根据Robert E Lucas（1978）模型[2]和消费的跨时Euler条件的观点：假设商品完全由不同的生产单位生产；生产过程外生于模型，完全由状态决定；产量服从马尔可夫过程。这些生产单位的所有权由竞争性股票市场决定。每个企业会发行一单位股票，这张股票是可以无限分割的，其红利就是产出的市场价值，是由外生马尔可夫过程决定的外生变量。股票在发放红利以后可在市场上进行交易。

一项资产的异常收益率是该资产的实际收益率与正常的投资收益率（指投资处于一种长期稳态时的均值，是由宏观经济变量所决定的收益率理性的部分）之差，异常收益率和对数异常收益率为

其中R0t和r0t分别是该参考资产的正常收益率和对数正常收益率。

在所建立的模型框架中，数据生成过程在两个状态间转换，而从一个状态到另一个状态的过程动态行为可以有很大的不同。进一步假设该过程受到两状态马尔可夫过程决定的离散转换的影响。观测到的时间序列zt来自两个不同的状态；St是潜在的随机变量，是一个未观测到的状态变量；t取离散值0，1，2，…；St取值为1，2，决定zt所处的不同的时域状态。为了便于讨论股市收益率状态，将股市的状态划分为无异常收益率状态Ⅰ和有异常收益率状态Ⅱ。设定St=1处于无异常收益率状态；St=2表示处于有异常收益率状态；抽取出来的均值和方差都是当时所处状态的函数；ztSt～N(μst,Ωst)，其中μst=(μ1, μ2)分别为zt在Ⅰ和Ⅱ时的均值，Ωst=(σ1, σ2)为状态依赖的标准差。利用“Hamilton过滤器”， 它服从一阶马尔可夫过程：

p11为当前期和前期都处于无异常收益率状态的经济概率，p12为从无异常收益率状态向有异常收益率转换的平滑转移概率，其中p11，p12，p21和p22为正的常数，满足p11+p12=p21+p22=1，于是得到该马氏链的状态转移矩阵P为

我们事先不能确定每一时刻经济处于何种状态的概率。该概率可能与t时刻前期的各个时刻所处的状态相关，即由t时刻前的各个时刻所处的状态决定在每一时刻t经济所处的状态。本文假定经济在状态Ⅰ和状态Ⅱ之间的变化服从马尔可夫过程（Markov Process简称马式过程），也即

此称为马尔可夫性。假定状态和时间都取有限个离散值，这种马式过程也称为马尔可夫链。当转移概率不受其他变量影响时，该马氏链称为齐次马氏链(Homogeneous Markov Chain)，利用齐次马氏链建立起来的模型则称为齐次马氏域变模型[6]。

为了方便求极大似然函数，可定义新的状态变量S*以表示t 时时域

t

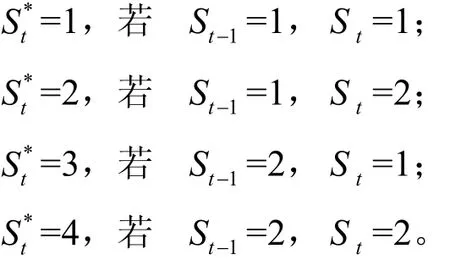
其中Ωt=(zt, zt−1，…,z0)，α=(μ1, μ2, σ1,σ2,p11,p22)刻画zt的概率密度特征的总体参数向量，用极大似然估计能最好地拟合数据的总体参数。

同理可求出S*=2，3，4 时异常收益率z的条件密度。

t t

全部样本ΩT的对数似然函数如下（具体推导过程见文献[7]）

其中

由于假定马氏链状态转移概率不变，因此马氏链状态转移矩阵P中的元素可作为PSt+1St的值。马氏链的平稳分布（当时间趋于无穷时，马氏链所收敛的分布）可取初始值P(S0)，设定的初始值直接影响算法的收敛速度，通过求出异常收益率所处状态和持久时间的无条件概率向量π可得到初始值。

尽管以上讨论的是二维马氏链，但对于多维马氏链实际上同样适用。

2 基于齐次马氏域变模型的上海股市异常收益率的实证检验

本节将以上证指数为主要研究对象讨论我国股市异常收益率。首先对收益率产生决定性影响的宏观经济变量进行单位根检验，接着使用Johansen协整检验方法从实际收益率中剔除其基础价值收益率决定部分,最后在两状态假设下运用齐次马氏域变模型进行检验。

2.1 对影响收益率的宏观经济变量进行单位根检验

“齐涨共跌”是我国股市明显存在的现象。由于宏观经济因素的影响在收益率的分析中作用明显，因此在收益率基础价值的研究中选择宏观经济变量作为解释因素[8]。

我们所选取的数据区间为1996年10月～2010年2月的月度数据，数据均来源于RESSET（锐思）金融研究数据库（http://www.resset.cn/）以及《中国经济景气月报》[由于2006年12月以后的工业增加值的月度数据不能从数据库直接得到，依据当月工业增加值=上年同期工业增加值×（当月比上年同期增长百分比+1）计算得到，2007，2008，2009，2010年1月的月度数据可用插值法得到]。首先，对上证指数及各宏观经济变量进行对数变换，并且对工业增加值、消费品价格指数和汇率进行X－11季节调整，用来消除序列中所存在的季节效应；然后对数据进行平稳性检验，结果如表1所示。

表1 经济变量序列的单位根检验结果Tab.1 Unit root test results of economic variables

检验结果表明，在5 %显著性水平下，样本期内所有序列都无法拒绝存在单位根的原假设，序列是非平稳的；对其差分序列进行平稳性检验，在1 %的显著性水平下，检验统计量均拒绝存在单位根的原假设，即所选变量序列在数据区间内均服从一阶单整变量，即I(1)过程。

2.2 基于Johansen协整检验方法剔除正常收益率

首先对相关宏观经济变量做协整回归，剔除不显著变量以及估计结果与经济实际意义不符的变量，由此可以尽量避免误设定异常收益率问题。对股市收益率影响最为明显是工业增加值（由于国民生产总值GDP的月度数据无法获得，故使用工业增加值对其进行替代）、准货币、无风险利率、汇率、消费品价格指数和上市公司净资产收益率，这些被选择组成宏观经济指标集来确定正常收益率部分。本文采用Johansen协整检验方法剔除正常收益率，若统计量的值低于临界值，则不能拒绝无协整关系的零假设。从表2中可以看出Johansen协整检验结果。虽然各经济指标是非平稳的一阶单整序列，金融资产收益变量和宏观经济变量具有长期均衡的协整关系。一般认为，当宏观经济因子变化和股价之间存在协整关系时，表明股票市场趋于稳定，市场正逐步走向有效和成熟；反之，若二者不存在协整关系，则预测市场可能仍然不成熟，需要利用法律等对交易主体进行规范。

表2说明，七个变量间存在显著的长期均衡关系，并在样本期内存在三个协整关系。λ−max统计量54.887 0(0.00) 49.077 1(0.01) 31.464 7(0.03) 26.664 8(0.07) 15.620 1(0.25) 8.383 0(0.34) 4.078 5(0.23)

表2 Johanson协整检验结果Tab.2 Johanson cointegration test results

如果按照传统的单位根和协整检验方法，可以拒绝在我国股市上存在异常收益率的原假设。然而，此种方法无法准确描述异常收益率的非线性路径和周期性变化。为了更准确地测定收益率的泡沫程度，将使用马氏域变方法对其进行分析。由于正常收益率在进行协整分析时已从收益率中剔除，因此只针对协整残差进行建模，而无需考虑残差均值。根据全样本区间内的协整残差路径，可以得出上证指数的协整残差就是tz，即是异常收益率。图1表明，协整残差中存在着明显的非线性特征，若使用线性模型进行分析,必然造成较大的误差。

图1 上证指数协整残差图Fig. 1 The shanghai stock index cointegration residual plot

2.3 基于两状态马氏域变模型的异常收益率验证

为了更本质地解释样本区间内估计母体参数的内在机理，假定上证指数中存在无异常收益率状态Ⅰ和有异常收益率状态Ⅱ，应用对数极大似然法对异常收益率进行估计。对数极大似然法通过Eviews 5.0的LogL编程实现，算法的收敛速度受初始值设定的直接影响。通过求出异常收益率所处状态和持久时间的无条件概率向量π可以得到初始值，得到表3。

从动态的角度，马氏域变模型研究股市收益率与波动性的对应关系，描述并证明了金融市场“收益与风险相对应”的特征。通过对上海股市进行实证研究，可知：

表3 上证指数异常收益率的域变模型的估计结果表Tab.3 Homogenous markov regimes switching model estimation results table of Shanghai Stock Index abnormal returns

1) 表中参数具有较小的方差，并且都落在各自的置信区间中，在一定程度上可以认为它们是一致的、鲁棒的；当前状态与前期状态均与模型中的波动率存在相关性，但真正原因尚待进一步研究；

2) 时域转换概率均小于8 %；在上证指数异常收益率的域变模型中，一个状态变为另一个状态的概率分别为p12=0.062 6（p12=1－p11），即无异常收益率状态继续的可能性为0.937 4，转为有异常收益率状态的概率为0.062 6（p12=1－p11），说明股市状态有很强的持续性；

3) 在1 %水平下两个参数均高度显著，序列波动率在两个状态下相差很大，有异常收益率状态与无异常收益率状态的方差之比为1.93倍，这暗含着不仅存在更大的波动性，更重要的是，潜伏着更大的冲击不确定性和金融风险；与其他模型相比，域变模型更好地解释了金融市场收益与风险相对应的基本特征，更深刻、准确地刻画股市收益率水平与股价波动风险的对称特征以及随机冲击持续性之间的动态关系。

对区间内各个时点考察得出上证指数处于有异常收益率状态的概率如图2所示。

图2 上证指数处于有异常收益率状态的概率Fig.2 Probability of shanghai stock index in abnormal returns

由于使用计量方法形成了样本损失，图中仅描绘出1996年12月到2010年2月间处于有异常收益率状态的概率，与同期上证指数序列(见图3)对照可以看到：

图3 上证指数Fig. 3 Shanghai stock index

2000年以前收益率泡沫情况较2000年大；从2000年以后股市陷入低迷，存在泡沫的概率均在30 %以下；泡沫概率在2006年后出现了逐渐增大的趋势，与2006年上半年股市逐渐走出熊市，股指开始上升的实际情况相符。

分析表明，2006年5月到2008年4月异常收益率的概率超过50 %。泡沫概率在2008年后逐渐减小，但也超过30 %。这与现实宏观环境相一致：我国经济当时发展迅速，人民币汇价不断提高，宏观经济面是可以解释收益率上涨的。可以看出宏观调控政策对我国股市影响较大，尤其是代表货币政策变化的控制变量，低弹性的货币政策调控减弱了控制变量对股市的影响。对于收益率时间序列的均值回复、波动聚集以及非线性特征，“依赖波动持久时间”现象具有很强的解释力。由波动性的低波动状态向高波动状态转移的时间点以及后续的持续时间上看，这些时间点大多位于监管当局加强监管力度或对股市实施政策影响的时候。明显的例子是2008年在我国股市受美国次贷危机的影响而导致大幅下跌后，央行实行了降息政策，致使一年期存款利率由4.14 %下降至2.25 %。

3 政策建议

由于异常回报率会在某种程度上对投资甚至对整体经济的运行造成较大影响，因此研究异常收益率对探索如何促进经济的稳定发展及可持续发展有着积极的意义。从上文分析可以看出，宏观调控和政府监管对股市影响较大，然而也不能忽略市场、上市公司和投资主体的影响，为此提出以下主要建议。

3.1 维持宏观调控的稳定性、货币政策的连续性，消除产生异常收益率的宏观因素

从上文对股票市场分析的结论及日本的金融危机可以看出政策的力度对股市影响较大。当指数迅速变化，股市泡沫可能被刺破或产生，股市由“牛”转“熊”或由“熊”转“牛”。出台货币调控政策时，不但要辅之以其他的有利措施，而且要注意货币政策制定的前瞻性和透明度，避免股市的大幅度波动，保证股票市场的稳定发展。

3.2 加强政府对证券市场的监管，消除制度性风险

当前我国证券监管体系还不太完善。政府用行政命令替代市场选择功能，过多地频繁干预二级市场的价格形成，导致监管手段偏于“政策化”，政府行政手段过于刚性。这些情况不但不利于我国证券市场的长远稳定发展，而且也深刻折射出我国市场存在着制度风险，即政府对市场参与主体的隐性担保和投资人对政府的寻租行为，所以要规范政府监管行为，消除制度隐患和风险。

3.3 健全市场法规，完善金融法律，促进市场的规范与透明

完善的法律法规是市场健康高效运行的基础和前提，因此要不断健全《证券法》、《公司法》和《证券交易法》等法律体系。规范透明的证券市场，有利于消除市场信息的不完全和不对称，抑制欺诈行为和内幕交易，改善市场的信息供给状况，有助于证券市场形成一个良性发展的交易环境，并可以在某种程度上消除新股的投机情绪，减少股市产生泡沫的概率。

3.4 提高上市公司的整体质量，完善上市退市制度

建立现代企业制度，完善法人治理结构，强化上市公司内部管理，改善上市公司股权结构的不合理，从而提高上市公司的整体质量，增加股票市场的可投资性。对于长期效益不好，经营或资产出现重大问题的上市公司，要严格执行中止上市或终止上市，强行督促上市公司提高自己的经营业绩，维护证券市场的健康运行。

3.5 加强投资者教育，使之形成正确的投资理念

投资者的非理性投资做法，不但会损害其自身的利益，而且破坏了市场的内在运行机制，因此政府要合理正确地引导股票市场主体的投资行为，避免“羊群行为”、“追涨杀跌”，进而可以有效地抑制泡沫的产生，促进股票市场稳健有序发展。

[1] 闫荣国 , 陈宇峰.基于马尔可夫域变模型的上海股市收益率非线性特征分析[J]. 统计与信息论坛, 2008(5):56-60.

[2] STEPHEN G C, POK-SANG L, NELSON C M. Mean reversion in equilibrium asset prices [J].The American Economic Review ,1990(60):398-418.

[3]HAMILTON J D, SUSMEL R. Autoregressive conditional heteroskedasticity and changes in regime [J]. Journal of Econometrics, 1994(64): 307-333.

[4]HAMILTON,J D. A new approach to the economic analysis of nonstationary time series and the business cycle [J].Econometrica,1989(57):357-384.

[5]MADDALA G S , RAO C R.金融中的统计方法[M]. 上海:上海人民出版社, 2004.

[6]孟庆斌,周爱民,汪孟海.基于齐次马氏域变方法的中国股市价格泡沫检验[J].金融研究,2008(8):105-118.

[7]HAMILTON J D著, 刘明志译.时间序列分析[M]. 北京:中国社会科学文献出版社,1999.

[8]江洲,谢赤.基于分布特征与宏观经济因素的证券市场收益率描述与预测[D]. 济南: 山东大学,2009.

[9]郭名媛,张世英.具有马尔可夫结构转换机制的波动模型及其应用[D]. 天津: 天津大学,2003.

[10]鲍未平,王金利.中国股票市场异常收益之实证研究[D]. 济南: 山东大学,2008.

[11] 黄辉,周孝华.IPOs长期异常收益率的度量方法及其实证研究[D]. 重庆: 重庆大学,2005.

[12]CHRIS B 著,邹宏元主译.金融计量经济学导论[M]. 成都:西南财经大学出版社,2005.

Analyzing and Testing for Abnormal Return of Shanghai Stock
with Homogenous Markov Regimes Switching Model

WU Jin-cun，FENG Wen-li，ZHANG Yue-hui
（Department of Finance, Hebei University of Economics and Business, Shijiazhuang 050061,Hebei Province, P.R.China）

Studies abnormal return by using homogenous Markov Regimes Switching Model and describes the nonlinear dynamics process of Shanghai Stock Index from October, 1996 to February, 2010. The author eliminates rational value component (normal return) based on Johansen Co-integration Test, and then constructs model of co-integrational residual error (abnormal return) by using homogenous Markov Regimes Switching Model and utilizes the method of Maximum Likelihood to estimate the reason. Finally, according to the analysis this paper indicates it is macro-economic policy factors that influence the abnormal return of China’s stock market , and propose corresponding policy suggestions.

abnormal return； Johansen co-integration test ； homogenous markov regimes switching model

F830.19

A

1001-4543(2010)02-0149-07

2010-04-28;

2010-06-11

武金存（1980－），女，甘肃金昌人，硕士研究生，研究方向为资本市场与证券投资，电子邮件：wujincun@yahoo.com.cn封文丽（1967－），女，河北平山人，博导，研究方向为资本市场与证券投资