在数学教学中培养学生的创新能力

广东省城市建设高级技工学校 钟利蕊

在数学教学中培养学生的创新能力

广东省城市建设高级技工学校 钟利蕊

创新能力的培养在数学教育方面可得到较为充分的体现,作为数学教师在教学过程中,培养学生的创新精神及独立分析问题,解决问题的能力,是当今社会对我们的要求,也是技校数学教学的主要任务之一,那么,怎样在数学教学中培养学生的创新能力呢?本文几点看法仅供参考,错误之处望指正。

联想类比猜想创新能力

一、从见微知著联想,引至新发现

在数学教学中,我们要让学生知道学习数学就是要有勇于探索,善于探索,见微知著,引致新发现的精神,并通过课堂教学对学生进行数学上见微知著的联想训练,掌握见微知著联想本领,从而培养学生的创新能力。

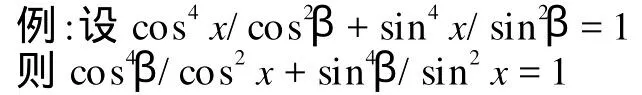
分析:我们发觉题中假设与sin2x+cos2x=1有点像,于是

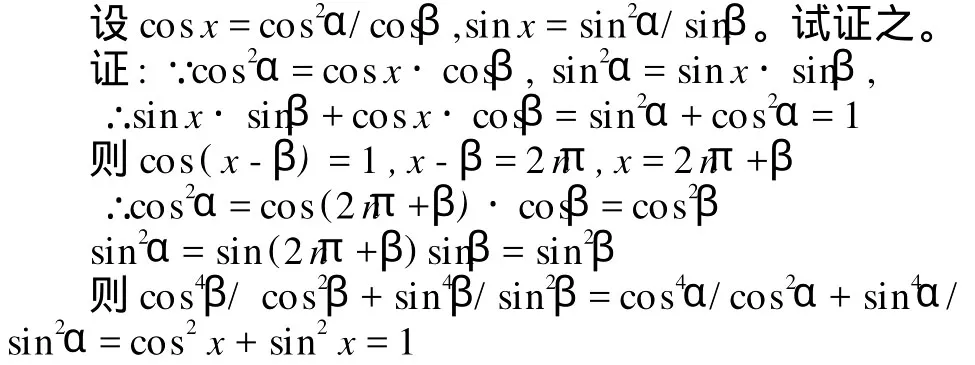
二、从类比推理猜想,解决新问题

一般地,当我们遇到一个新问题的时候,联想一个已经解决的旧问题,新问题与旧问题有某些类似的特征,于是可以猜想:新问题和旧问题可能有某些类似的结论,或者可能用解决旧问题的类似办法解决新问题。这种寻求解决问题途径的思考方法,我们称为类比推理方法。科学上的许多重要发明都与这种类比推理法有关。故此,类比推理法是人们的一种非常重要的思考方法。在数学教学上,遇到一个数学问题时,常常运用类比推理法,联想一个已经解决的数学问题,从中得到启发,找到新问题的解决方法。譬如:

1.条件结论的类似

我们注意到,立体几何中的一些问题,可通过类比平面几何中的类似问题而得到解决。事实上,立体几何中的一些命题,就是把平面几何中相应命题的“点、线、面”分别换成“线、面、体”而得到的。

例:证明正四面体内的任意一点到各面的距离之和为定值。我们要告诉学生:当你看到这道题的时候,你是否联想到平面几何中的一道题:“证明三角形内的任意一点到各边的距离之和为定值”。这两道题多么相似!在平面几何中已经得到这样的结论:正三角形内的任意一点到各边的距离之和等于它的高。如果我们回忆起这个结论的时候,可能很快就想到:正四面体内的任意一点到各面的距离之和是否也等于它的高呢?这个猜想是对的。

2.结构形式的类似

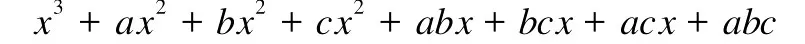
例:分解因式分析:这个多项式在结构形式上与x2+ax+bx+ab类似,可进行如下分解:

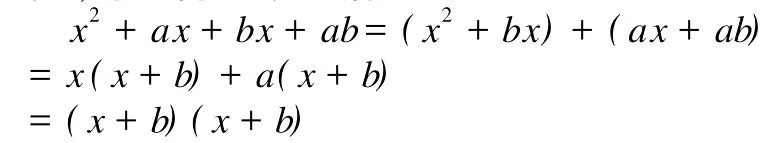
我们观察到该式分解的特点是:把含有字母a的项分为一组,其余的项分为一组,然后采用分组分解法。运用类比的方法受到启发;对于原来的多项式,也可先把含有字母a的项分为一组,其余的项分为一组,现进行如下分解:

在教学过程中,我们运用类比方法培养学生类比推理猜想的能力,有助于学生主动地探求和获取知识,有助于培养学生创新思维能力。

三、从特殊化猜测,发现新思路

在数学中,我们常把一个问题特殊化,通过特殊化的猜测,得到启发,从而探索到一般规律,发现问题的新思路。

例:已知a1,a2,…an是n个正数。证明

我们先考察n=3的特殊情形。这时利用不等式

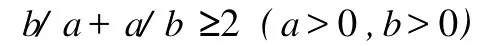
便可以得到

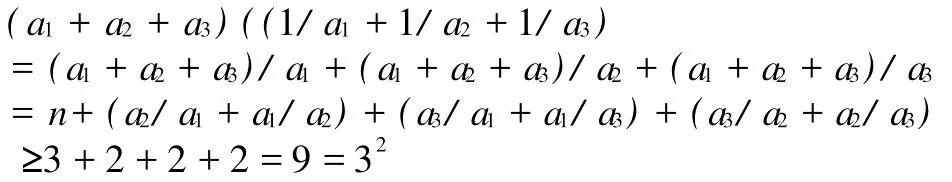
由这种特殊化猜想,得到一般情形的证明方法:证:利用不等式

可能得到:

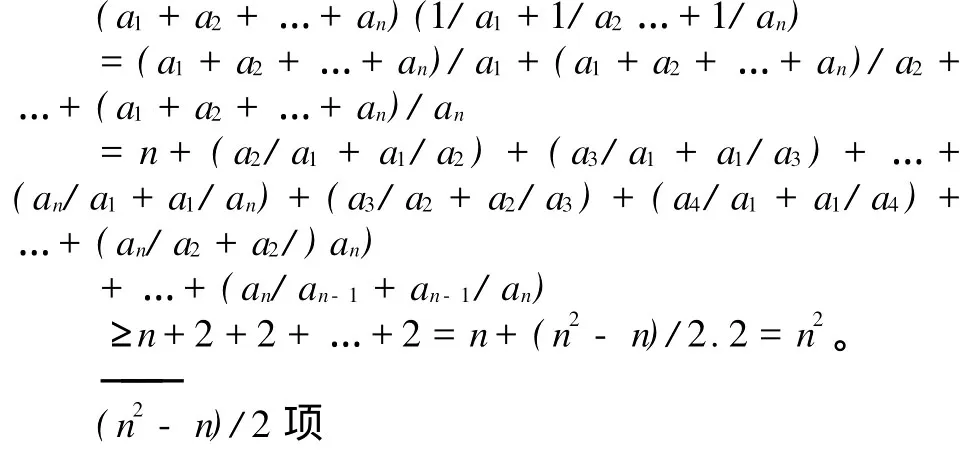
此例的求证方法可启发学生:有时有些问题的求解可从特殊性到一般性的思考方法来发现新思路。

学生创新能力的培养是多方面的,方法也有很多。以上只是就在数学教学中如何着力培养学生创新能力问题谈自己的几点看法,仅为抛砖引玉。作为数学教师,我们应鼓励、引导学生大胆猜想、怀疑、创造,创设生动活泼,师生互动的课堂气氛,为培养具有创新精神和能力的学生而不断探索、进取。

[1]朱匀华.中学数学思考方法与解题技巧

book=271,ebook=203